7.1 Triangle and its Angles
A triangle is a closed figure bounded by three straight lines. A triangle is denoted by the symbol .
In the figure, XYZ is a triangle with XY, YZ and ZX as sides and X, Y, Z are called the vertices of the triangle XYZ.
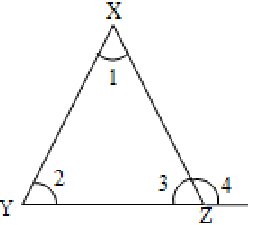
are the interior angles
The sum of the three interior angles of a triangle is 180°.
are the interior opposite angles and is the interior adjacent angle with respect to .
Types of Triangles with respect to their Angles
1. Right-angled Triangle
The side opposite to the right angle is called the hypotenuse and it is the longest side.
The sum of the other two angles is equal to 90°. When the other two angles are equal, then the other two sides are also equal. = 90° , = and are necessarily acute.
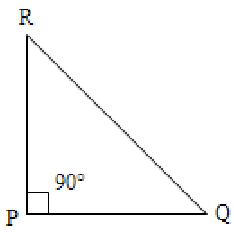
Note: The sides forming the right angle are called the legs of the right angle.
2. Acute-angled Triangle
When all the three angles are equal, then all the three sides are also equal.
3. Obtuse–angled Triangle:
90° A < 180°, ?B and ?C are necessarily acute.
Types of Triangles with respect to their sides
1. Equilateral Triangle
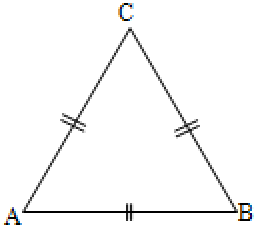
When all the three sides are equal, then all the three angles are also equal. Since all the three angles are equal, this triangle is also called an equiangular triangle.
Note: Here each angle is 60°.
2. Isosceles Triangle
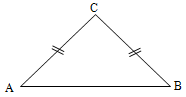
AC = BC AB.
The angles opposite to these two sides are also equal.
Note: Opposite angles of equal sides are equal.
3. Scalene Triangle:
When all the three sides are different , the three angles are also different. In any triangle the maximum number of acute angles that can be drawn are three, and minimum are two.
Acute Angles are necessary in a Triangle.
Only one right angle (or) one obtuse angle is possible in any triangle.
Exterior Angle
If the side BC of a ABC is extended to D to form a ray BD, then ACD is called an exterior angle of ABC angled at C and is denoted by the exterior angle, ACD.
Interior Angle
The angles A and B are called the remote interior angles or the interior opposite angles of the exterior angle ACD. The sum of the interior opposite angles is equal to the exterior angle formed.
A + B = ACD
The exterior angle is greater than each of the interior opposite angles.
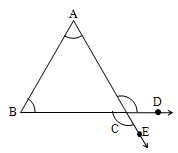
If the side AC is extended to E to form a ray AE, then BCE is an exterior angle of ABC. From above, we can conclude that at each vertex of a triangle there exist two exterior angles.
In the above figure in ABC, the exterior angles ACD and BCE are equal as they are vertically opposite angles i.e., ACD = BCE. The two interior opposite angles will be the same for the two exterior angles formed at a particular vertex.
Proof: 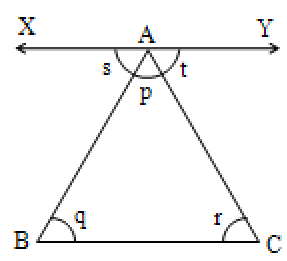
Given ABC is a triangle. The interior angles of this triangle are , and .
It is required to prove that the sum of the three interior angles is 180°. i.e. p + q + r = 180°.
Through A, draw a line XY parallel to BC.
s and t are the exterior angles on the line XY at point A.
Since XY is parallel to BC.
( alternate interior angles)
Adding p on both the sides,
we get
But 180° (by linear pair axiom)
180°
180°
Hence the sum of the three interior angles of a triangle is 180°.
Proof: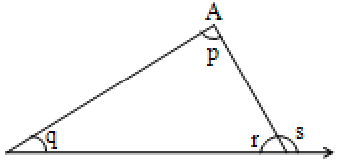
Consider a ABC, with angles p, q and r. Extend the side BC to D.
Let the exterior angle at ‘C’ be ‘s’.
It is required to proved that
From Interior angle theorem, we have
= 180° ______ (1)
Also = 180° ______ (2) ( linear pair)
From (1) and (2), we have
Hence the exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Importance of Interior and Exterior Angle Theorems
1. The interior angle theorem involves the three angles inside a triangle. It states that together they make 180°.
2. Making use of alternate angles and linear pair of angles made by a transversal on straight lines, we prove that the sum of the three angles in a triangle is 180°.
3. The exterior angle theorem involves an external angle formed by the extension of one side of the triangle in addition to the two interior angles opposite to it.
4. We make use of the interior angle theorem and the exterior angle is equal to the sum of the two interior opposite angles.
Exterior angles = Sum of the two interior opposite angles.
Properties of a Triangle
1. The sum of the three interior angles of a triangle is 180°.
2. In a triangle, the sides opposite to the angles of equal measure are of equal length.
3. The angles opposite to the sides of equal length are of equal measure, in a triangle.
4. In a triangle, the measure of an exterior angle is equal to the sum of the measures of the interior opposite angles.
7.2 Congruence of Triangles
Two geometrical figures are said to be congruent if they have exactly the same shape and size.
Congruency is denoted by the symbol .
1. Two line–segments are said to be congruent, if and only if their lengths are equal.
Eg:
AB CD
2. Two angles are said to be congruent if, and only if, their measures are equal.
Eg:
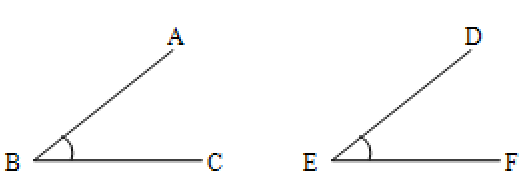
ABC DEF
m ABC = m DEF
3. Two triangles are said to be equal in all respects, when one is placed on the other to exactly coincide with it, in which each part of the first triangle is equal to the corresponding part of the other.
Also the triangles are equal in area.
The method of testing equality is known as the method of superimposition. The triangles which are made to coincide by superimposition are said to be congruent or identically equal.
Eg:
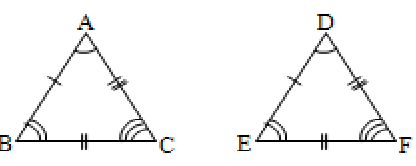
Here, A D, B E and C F
Two triangles ABC and DEF are said to be congruent if, and only if, there is a correspondence between their vertices such that the corresponding sides and the corresponding angles are equal. Congruent triangles are similar but similar triangles are not congruent always.
Congruent triangles Similar triangles
Similar triangles Congruent triangles
Properties of Congruent Relation
From the above example ABC DEF
1. Congruence Relation is Reflexive:
ABC ABC
2. Congruence Relation is Symmetric:
If ABC DEF, then DEF ABC
3. Congruence Relation is Transitive :
Suppose there is a third triangle XYZ which is congruent to DEF.
If ABC DEF and DEF XYZ then ABC XYZ.
7.3 Criteria for Congruence of Triangles
1. SAS (side – angle – side) Congruence Axiom
The axiom states that two triangles are congruent if any two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle. 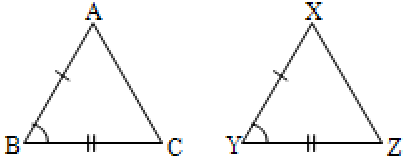
If AB = XY
B = Y and BC = YZ then ABC XYZ.
Note: The included angle must be the angle formed by the two equal sides, otherwise the triangles may not be congruent.
2. ASA (angle – side – angle) Congruence Axiom
In this axiom, two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. 
If A = D; AC = DF and C = F then ABC DEF.
Note: The included side is the side edged by the two angles.
3. AAS (angle – angle – side) Congruence Axiom (corollary of ASA Axiom)
If any two angles and a non – included side of one triangle are equal to the corresponding two angles and the non – included side of the other triangle, then the two triangles are congruent. 
If A = D; B = E; AC = DF then ABC DEF.
4. SSS (side – side – side) Congruence Axiom
In this axiom, two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.
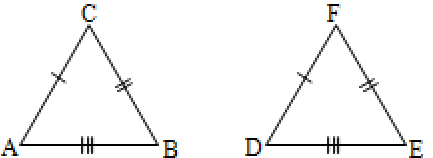
If AB = DE; BC = EF; AC = DF then
ABC DEF.
5. RHS (right angle – hypotenuse – side) Congruence Axiom:
In this axiom, two right triangles are congruent if the hypotenuse and one side of a triangle are respectively equal to the hypotenuse and the corresponding side of the other triangle.
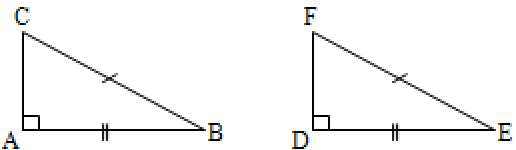
If A = D = 90°; AB = DE and BC = EF then ABC DEF.
Note: AAA is not a criterion for congruence of triangles, since the lengths of the sides need not be equal in triangles of equal angles.
7.4 Congruent Triangles-Theorems
Proof
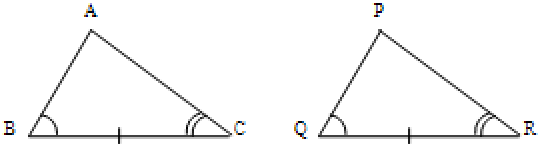
Let the two triangles be ABC and PQR.
Given that, B = Q, BC = QR and C = R
It is required to prove that ABC PQR.
Case (i)
If AB = PQ, we also have BC = QR and B = Q, then by SAS congruence axiom
ABC PQR
Case (ii)
Suppose AB PQ. Let AB < PQ.
Take a point S on PQ such that QS = AB. Join RS.
Now in ABC and SQR,
By SAS axiom
This is impossible unless RS coincides with RP or S coincides with P.
AB must be equal to PQ.
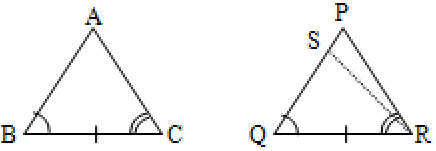
Case (iii)
If we suppose that AB > PQ, then a similar argument applies and ABC PQR
Hence, in all the cases ABC PQR.
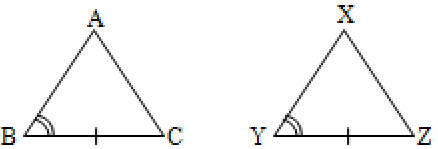
Let the two triangles be ABC and XYZ.
Given that A = X, B = Y and BC = YZ
It is required to prove that ABC XYZ
Since the sum of the three angles of a triangle is 180°,
A + B + C = 180° and X + Y + Z = 180°
But, and
In ’s ABC and XYZ
and BC = YZ
By ASA congruence theorem,
Proof
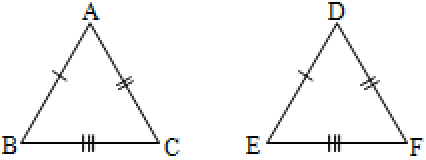
Let the two triangles be ABC and DEF.
Given that AB = DE, BC = EF and CA = FD
It is required to prove that
Suppose BC is the longest side.
Draw EG from E such that EG = AB
Join FG and DG
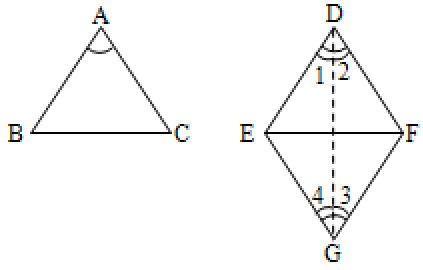
In ’s ABC and GEF
AB = GE
and BC = EF
By SAS axiom,
and AC = GF
Now AB = DE and AB = GE
DE = GE
Similarly, we can prove that DF = GF
Now in EDG, DE = EG
( angles opposite to equal sides of a triangle are equal)
And in DFG, DF = GF
( angles opposite to equal sides are equal)
i.e.,
But
Now in , AB = DE
AC = DF and
By SAS congruence axiom
.
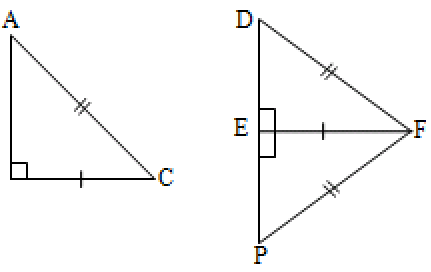
Let the two triangles be ABC and DEF.
Given in ’s ABC and DEF,
AC = DF and BC = EF.
It is required to prove that .
Produce DE to P such that EP = AB. Join FP.
Now in ’s ABC and PEF,
AB = EP, BC = EF and ABC = PEF
(By SAS axiom)
and AC = PF
Also AC = DF PF = DF
Now in DFP, DF = PF
( angles opposite to equal sides are equal)
But
In ’s ABC and DEF
Now in ’s ABC and DEF,
we have BC = EF
C = F and AC = DF
By SAS axiom
.
Important Concepts
1. Two triangles are congruent if they have exactly the same shape and size.
2. Congruence relation is equivalent i.e., reflexive, symmetric and transitive.
3. Congruence axioms are:
i) SAS (side – angle – side) :
Two sides and included angle of ABC = Corresponding two sides and included angle of PQR.
ii) ASA (angle – side – angle) :
Two angles and included side of ABC = Corresponding two angles and included side of PQR.
iii) AAS (angle – angle – side) :
Two angles and non-included side of ABC = Corresponding two angles and non-included side of PQR.
iv) SSS (side – side – side) :
Three sides of ABC = Corresponding three sides of PQR.
v) RHS (right angle – hypotenuse – side) :
Hypotenuse and one side of ABC = Hypotenuse and corresponding side of PQR.
7.5 Some Properties of a Triangle
Equilateral triangle:
A triangle is called an equilateral triangle if and only if all its three sides are equal.
In ABC,
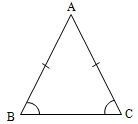
Isosceles triangle:
A triangle is called an isosceles triangle if and only if at least two of its sides are equal. Angles opposite to the equal sides are also equal. The equal angles are called the base angles and the other angle is called the vertical angle.
In an isosceles triangle, the unequal side is called the base of the triangle.
In ABC,
An equilateral triangle is also an isosceles triangle.
Whereas an isosceles triangle is not an equilateral triangle.
Proof
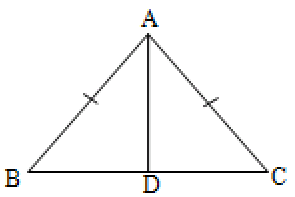
Given ABC is a triangle in which AB = AC.
It is required to prove that B = C
Draw AD BC
Consider the triangles AB D and ACD.
We have ADB = ADC = 90°
AB = AC (given) and AD is the common side
By R.H.S. congruence theorem,
ABD ACD. Hence B = C
Hence angles opposite to the equal sides of a triangle are equal.
( corresponding angles of congruent triangles are equal.)
Proof
Given ABC is a triangle and B = C.
It is required to prove that AB = AC
Draw AD BC.
In the triangles ABD and ACD, we have
B = C (Given)
ADB = ADC = 90° and AD is the common side
By R.H.S. congruence theorem.
ABD ACD. Hence AB = AC.
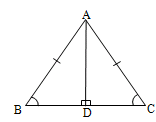
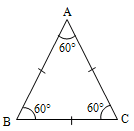
Proof
Given that in ABC,
It is required to prove that
A = B = C = 60°
Let us apply Theorem 18.
In ABC,
B = C _______ (1)
Also
A = C _______ (2)
Since the sum of the three interior angles of a triangle is 180°,
A + B + C = 180° _______ (3)
But from (1) and (2) we get
A = B = C _______ (4)
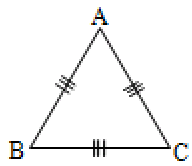
From (3) and (4)
A = 180° A = 60°
A = B = C = 60°.
Hence proved.
An isosceles triangle is a triangle with atleast two of its sides equal. If two sides are equal, then the angles opposite to them are equal.
Also, if two of its angles are equal, then the sides opposite to them are equal.
An equilateral triangle has all its sides equal. Moreover, all the three angles are equal and each angle is 60°.
Important Concepts
1. A triangle with all its sides equal is an equilateral triangle.
2. A triangle with atleast two sides equal is an isosceles triangle.
3. Equilateral triangle can be an Isosceles triangle
Isosceles triangle need not be an Equilateral triangle
4. In an equilateral triangle all the three angles are equal and each is 60°.
5. In an isosceles triangle, Two sides are equal
angles opposite are equal
Two angles are equal sides opposite are equal
7.6 Inequalities in a Triangle
Theorem. If two sides of a triangle are unequal, the longer side has greater angle opposite to it.
Activity : We draw a line segment AB. We draw an arc with A as centre and with the same radius and mark different points , , , and on it.
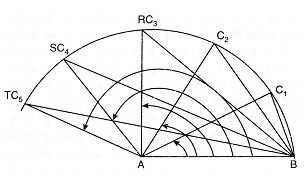
Proof: We join each of these points with A as well as with B. We observe that angle A is becoming larger and larger length of the side opposite to angle A becomes longer and longer.
AB > AB > AB > AB > AB.
And B > B > B > B > B
Now, we arrive at the conclusion as stated below :
Theorem. If two angles of a triangle are unequal, the greater angle has the longer side opposite to it.
Proof: We draw a triangle ABC and produce BA to a point u such that AD = AC.
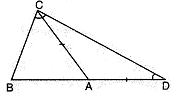
we observe that BCD > BDC.
It shows that side BD > side BC
AB + AD > BC
From the above discussion we arrive at the result as stated below :
Theorem. The sum of any two sides of a triangle is greater than the third side.
7.7 Concurrent lines in a Triangle
If a number of straight lines intersect at one common point, they are called concurrent lines.
Altitude
In a triangle, the perpendicular drawn from a vertex to its opposite side is called an altitude.
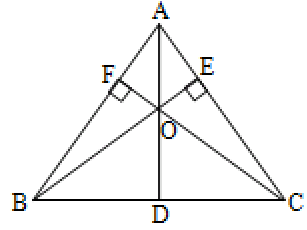
In the above figure, AD, BE and CF are the three altitudes of ABC. The three altitudes of a triangle always meet at a single common point called the orthocentre, denoted by ‘O’ which can lie inside or outside the triangle. In a right – angled triangle it lies at the vertex containing the right angle. In an isosceles triangle it lies on the altitude drawn to the base.
Median
The straight line joining any vertex to the midpoint of the opposite side of a triangle is known as a median.
In the figure below, AF, BE and CD are the medians of ABC.
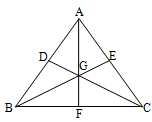
The three medians meet at a common point called the centroid of the triangle and is denoted by G. Centroid is the centre of gravity of all the triangles. Centroid divides each median in the ratio of 2 : 1. A median divides a triangle into two triangles of equal area.
Angular bisectors
The line-segments which bisect the angles of a triangle are called the angular bisectors. The line-segments which bisect the angles of a triangle internally are called the internal bisectors. In the figure below, AD, BE and CF are the angular bisectors of ABC.
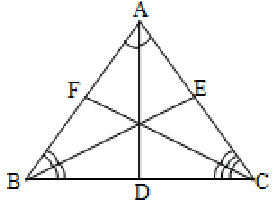
Incentre
The point through which all the internal bisectors pass is called the incentre of the triangle and is denoted by ‘I’. It always lies inside the triangle. In an isosceles triangle it lies on the altitude of the base. It is always equidistant from the sides of the triangle. The circle drawn with ‘I’ as centre and touching all the three sides of the triangle is called the incircle. The radius of the circle is called inradius and is denoted by ‘r’.
Excentre
The external bisectors of B and C and internal bisector of A are concurrent at called Excentre.
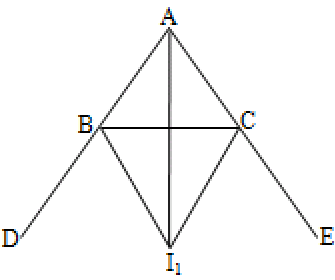
The excentre is opposite to A. Similarly, there are another two excentres and opposite to B and C.
Perpendicular Bisectors
The lines that are perpendicular and passing through the midpoint of the sides of a triangle are called the perpendicular bisectors of the sides. Perpendicular bisectors need not pass through the opposite vertex. The point through which the perpendicular bisectors pass is called the circumcentre and is denoted by ‘S’.
It can be inside or outside the triangle. In an obtuse-angled triangle, the circumcentre lines outside of it. In a right-angled triangle it lies on the midpoint of the hypotenuse. In an isosceles triangle it lies on the altitude of the base. By taking ‘S’ as centre, we can draw a circle which passes through all the three vertices. Such a circle is known as the ‘circumcircle’. Radius of the circumcircle is called the ‘circumradius’ i.e., denoted by ‘R’.
Nine point circle
A circle passes through the nine points given below which are very specific to the triangle. They are :
From the figure:
1. Midpoints of sides BC, AC and AB are X, Y and Z.
2. Feet of the altitudes are D, E and F (altitudes).
3. Midpoints of line-segments joining the vertex and the orthocentre(O) are P, Q and R.
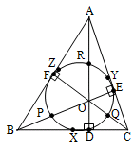
Properties
1. The medians of a triangle are concurrent.
2. The perpendicular bisectors of the sides of a triangle are concurrent.
3. The altitudes of a triangle are concurrent.
4. The angular bisectors of a triangle are concurrent.
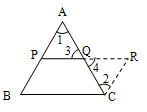
Proof
In ABC, P and Q are the midpoints of the sides AB and AC.
It is required to prove that PQ || BC and
Extend PQ to R, such that PQ = QR. Join CR.
Now in ’s APQ and QRC,
AQ = QC ( Q is the midpoint of AC)
AQP = CQR ( vertically opposite angles) and PQ = QR
By SAS congruence axiom,
APQ QRC
AP = CR
But AP = PB ( P is the midpoint of AB)
PB = CR
Also since APQ QRC
PAQ = ACR
But these are alternate angles
BP || CR
Since BP is equal and parallel to CR, BCRP is a parallelogram.
PR || BC ( opposite sides of a parallelogram are parallel)
PQ || BC and PR = BC ( opposite sides of a parallelogram are equal)
Thus the line-segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
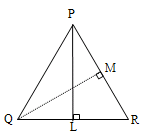
Proof
Given, PQR is a triangle and altitudes PL and QM are equal. It is required to prove that PQR is isosceles.
Consider right–angled triangles PLR and QMR
PL = QM (given)
R is the common angle
PLR = QMR = 90°
Using AAS congruence axiom,
PLR QMR. Hence PR = QR
PQR is an isosceles triangle.
Proof
Let ABC be a triangle with AB = AC .
It is required to prove that BD = CE.
Consider CEB and BCD.
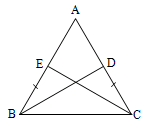
Here BC is the common side
BE = DC (halves of equal sides)
BCD = CBE ( In a triangle, angles opposite to equal sides are equal)
By SAS congruence axiom.
BDC CEB
Thus BD = CE.
Key Concepts
1. A line-segment which joins the midpoints of two sides of a triangle is parallel to the third side and is equal to half of it.
2. A triangle is isosceles if two altitudes are equal.
3. In an isosceles triangle the medians on the equal sides are equal.
4. Concurrent lines are a number of straight lines that intersect at one common point.
5. Altitude is the perpendicular drawn from a vertex to its opposite side in any triangle.
6. Ortho centre is the point at which the three altitudes of a triangle meet.
7. Median is a straight line drawn from a vertex to the midpoint on its opposite side, in any triangle.
8. Centroid is the point at which the three medians of a triangle meet.
9. The line-segments which bisect the angles of a triangle are called angular bisectors.
They are internal, external are perpendicular.
Note: In a right triangle the median drawn to the hypotenuse is equal to half of the hypotenuse.
Summary of Triangles
|
Symbol used |
Appearance |
Components |
Types |
Congruency |
Congruence relation |
|
Closed |
3 vertices 3 slides 3 angles |
Equilateral Isosceles Scalene Right – angled Acute – angled Obtuse -angled
|
SAS axiom ASA axiom AAs axiom SSS axiom RHS axiom |
Reflexive Symmetry Transitive |
|
Equilateral |
Isosceles |
|
3 equal sides 3 equal angles Each angle = |
Two sides equal Two sides equal Opposite two angles equal Two angles equal Opposite two sides equal |
|
Special lines |
Occurence |
Concurrence |
Symbol |
|
Altitude |
Perpendicular from vertex to the opposite side |
Orthocentre |
O |
|
Median |
Straight line from vertex to the midpoint of opposite side |
Centriod |
G |
|
Angular bisector |
Line-segment bisecting the angle |
Incentre |
I |
|
Perpendicular bisector |
Perpendicular passing through the midpoints |
Circumcentre |
S |
Important Concepts
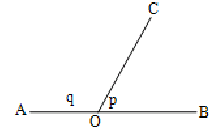
1. If a line stands on another line the sum of the two adjacent angles, called a linear pair, is equal to 180° i.e., p + q = 180° i.e., p + q = 180°. Conversely if p + q = 180°, AB is a straight line.
2. The bisectors of the adjacent angles of a linear pair enclose a right angle POQ = 90°.
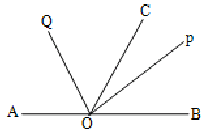
3. When a number of straight lines meet at a point the sum of the angles so formed at the point is equal to 360°.
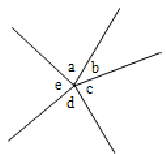
4. If two straight lines intersect one another, then vertically opposite angles are equal. In the figure p = r and q = s.
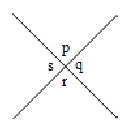
5. If two parallel lines are intersected by a transversal then
(i) Corresponding angles are equal
(ii) Alternate angles are equal
(iii) Interior angles on the same side of the transversal are supplementary.
= (corresponding angles)
= (alternate angles)
+ = 180°
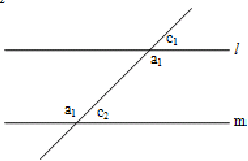
6. Conversely, if a transversal intersects two straight lines such that
(i) a pair of corresponding angles are equal or
(ii) a pair of alternate angles are equal or
(iii) a pair of interior angles on the same side of the transversal are supplementary, then the two lines are parallel.
7. If there are three or more parallel straight lines and the intercepts made by them on any transversal are equal, then the corresponding intercepts on any other transversal are also equal.
8. The sum of the three angles of a triangle is two right angles.
9. The exterior angle of a triangle is equal to the sum of the two interior opposite angles.
10. In a right triangle the median drawn to the hypotenuse is half of the hypotenuse. In the figure B = 90°, BD is the median.
AD = BD = DC.
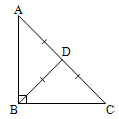
11. Conversely, in a triangle, if a median drawn to a side equals half of that side, then the triangle is right -angled.
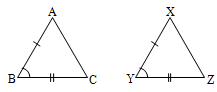
12. Two triangles are congruent, if and only if, all the sides and angles of the one are equal to the corresponding sides and angles of the other.
13. SAS axiom: If two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other, then the triangles are congruent.
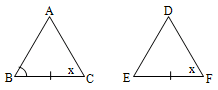
14. ASA axiom: if any two angles and the included side of one triangle are equal to the corresponding angles and the included side of the other triangles then the triangles are congruent.
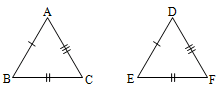
15. ASA axiom: If the three sides of a triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent.
16. RHS axiom: In two right triangles if the hypotenuse and a side of one triangle are equal to the hypotenuse and the corresponding side of the other then the two triangles are congruent.
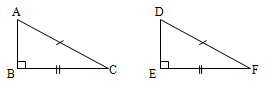
17. In an isosceles triangle;
(i) The angles opposite to equal sides are equal.
(ii) The sides opposite to equal angles are equal.
18. In an equilateral triangle all the three angles are equal and each is 60°.
19. In an isosceles triangle, the centroid, circumcentre, incentre, orthocentre are collinear whereas in an equilateral triangle these points coincide.








