Heron’s Formula

6.1 INTRODUCTION
In our earlier classes, we have studied various plane figures such as triangles, quadrilaterals, squares, rhombus, rectangles etc. Here we study a special & well known formula known as Heron’s Formula for calculating area of a triangle in terms of its three sides. First of all we will recall some basic concepts which were learnt in earlier classes. Perimeter
The perimeter of a plane figure is the length of its boundary, so it is the total distance around the outside of a shape. The perimeter of a triangle or a polygon is the sum of the lengths of its sides.
The unit of length is also the unit of perimeter i.e. centimetre, metre, kilometre etc. Area
The amount of space inside the shape is called its area. So the area of a plane figure is the measure of the surface enclosed by its boundary.
The units of area are ${\mathrm{cm}}^2,{\mathrm{m}}^2$ etc.
6.2 Perimeter and Area of different types of triangles
1. Right Angled Triangle
Let $∆\mathrm{ABC}$ be a right angled triangle in which $\angle \mathrm{B}=90°$ , then
(i) Perimeter = AB + BC + AC
(ii) Area = $\frac{1}{2}$ × Base × Height

= $\frac{1}{2}\times (\mathrm{BC}\times \mathrm{AB})$
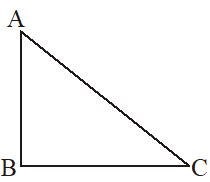
(iii) ${\mathrm{AC}}^2={\mathrm{AB}}^2+{\mathrm{BC}}^2$ (Pythagoras Theorem)
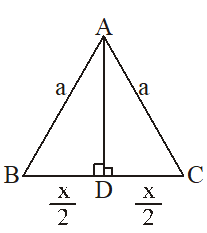
2. Isosceles Triangle
Let $∆ABC$ be an isosceles triangle in which AB = AC = a and BC = x. Let  $\mathrm{AD}\perp \mathrm{BC}$ then,
(i) Perimeter = AB + BC + AC = 2a + x
(ii)Area= $\frac{1}{2}$×Base×Height = $\frac{1}{2}\times \left(\mathrm{x}\times \sqrt{{\mathrm{a}}^2–\frac{{\mathrm{x}}^2}{4}}\right)$

3. Equilateral Triangle
Let be an equilateral triangle in which AB = BC = AC = a
(i) Perimeter = 3a
(ii) Altitude = $\frac{\sqrt{3}}{2}\mathrm{a}$

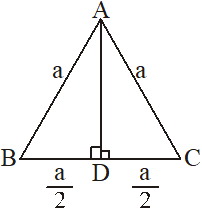
(iii) Area = $\frac{\sqrt{3}}{4}{\mathrm{a}}^2$
6.3 Area of a Triangle– by Heron’s formula
Heron was born in about 10AD in Alexandria in Egypt. His work on mathematical and physical subjects is so numerous and varied that he is considered to be an encyclopedia writer in these field. His geometrical work deals largely with problems on mensuration. The formula given by Heron is a famous formula for calculating area of a triangle in terms of its three sides. Let a, b and c are the sides of the triangle and s is semi-perimeter i.e. $s=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$ then,
This formula can be used for any triangle to calculate its area and it is very useful where it not possible to find the height of the triangle easily. Heron’s formula is generally used for calculating area of scalene triangle.
Example 1
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find
(i) the area of the triangle, and
(ii) the height corresponding to the longest side
Solution
(i) Let the given triangle be and let the sides of the triangle are 3x, 4x and 5x cm then
Perimeter = 3x + 4x + 5x
$\Rightarrow 144=12\mathrm{x}$
$\Rightarrow \mathrm{x}=\frac{144}{12}$
$\Rightarrow \mathrm{x}=12 \mathrm{cm}$
then, sides of the triangle will be a= 3×12 = 36 cm b = 4 × 12 = 48 cm and c = 5 × 12 = 60 cm
We have $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}=\frac{36+48+60}{2}$

$=\frac{144}{2}=72 \mathrm{cm}$
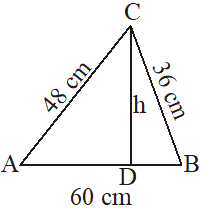
Using Heron’s formula, area of  $△\mathrm{ABC}$
$=\sqrt{\mathrm{s}(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})}$
$=\sqrt{72(72–36)(72–48)(72–60)}$
$=\sqrt{72\times 36\times 24\times 12}$
$=\sqrt{(12\times 12)(12\times 12)(6\times 6)}=12\times 12\times 6$
$=864{ \mathrm{cm}}^2.$
(ii) Let the height corresponding to the longest side is h then
area of $\mathrm{\Delta ABC}$ = $\frac{1}{2}$ × Base × Height
864 = $\frac{1}{2}\times 60\times \mathrm{h}$

h = $\frac{864}{30}$

h = 28.8 cm. Hence, the height corresponding to the longest side is 28.8 cm.

Example 2
The sides of a triangular field are 165 cm, 143 cm and 154 cm. Find the cost of the ploughing it at 12 paise per sq. m.
Solution
Let the sides of the triangular field are a = 165 cm, b = 143 cm and c = 154 cm
We have s = $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$
$=\frac{165+143+154}{2}=\frac{462}{2}=$231 cm
Now, by Heron’s formula area of the triangular field = $\sqrt{\mathrm{s}(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})}$
$=\sqrt{231(231–165)(231–143)(231–154)}$
$=\sqrt{231\times 66\times 88\times 77}$
$=\sqrt{11\times 7\times 3\times 11\times 3\times 2\times 11\times 8\times 11\times 7}$ $=11\times 11\times 7\times 3\times 2\times 2=10164{ \mathrm{cm}}^2$
Given that cost of ploughing is 12 paise per ${\mathrm{m}}^2$ cost of ploughing the triangular field
= 10164 × 12 paise
= Rs.$\frac{10164\times 12}{100}=\frac{121968}{100}$= Rs. 1219.68
Hence, cost of ploughing the triangular field is Rs. 1219.78.
Example 3
Find the area of a trapezium whose parallel sides are 55 cm, 40 cm and non parallel sides are 20 cm, 25 cm.
Solution
Let ABCD be the given trapezium with AB||DC then
AB = 55 cm, CD = 40 cm
AD = 20 cm and BC = 25 cm

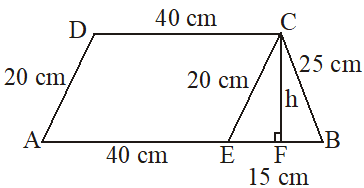
We draw CE || DA and complete the parallelogram AECD. Then CE = 20 cm and AE = 40 cm.
Also, BE = AB – AE
BE = (55 – 40) cm
BE = 15 cm
Let $\mathrm{CF}\perp \mathrm{AB}$ such that CF = h cm
Now, in
a = 20 cm, b = 25 cm and c = 15 cm
$\therefore$ s = $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$
= $\frac{20+25+15}{2}=\frac{60}{2}$ = 30 cm
By Heron’s formula, we have area of $\mathrm{\Delta BCE}=\sqrt{\mathrm{s}(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})}$ $=\sqrt{30\times (30–20)\times (30–25)\times (30–15)}$
$=\sqrt{30\times 10\times 5\times 15}$
$=\sqrt{10\times 3\times 10\times 5\times 5\times 3}$
$=10\times 3\times 5=150{ \mathrm{cm}}^2$
Also, area of $\mathrm{\Delta BCE}=\frac{1}{2}$ × Base × Height
150 $\frac{1}{2}\times 15\times \mathrm{h}\Rightarrow \mathrm{h}=20$ cm
Now area of trapezium = $\frac{1}{2}$ × (sum of parallel sides) × height $=\frac{1}{2}\times (40+55)\times 20=95\times 10=950{ \mathrm{cm}}^2$
Hence, area of given trapezium is 950 cm2.
6.4 Some important formulas related to plane figures.
1. Rectangle
Let ABCD be a rectangle with length l and breadth b, then
(i) Perimeter = 2 (l + b)
(ii) Area = l × b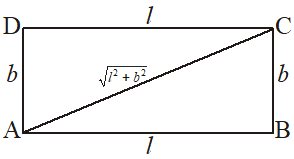

(iii) Diagonal = $\sqrt{l^2+{\mathrm{b}}^2}$
2. Square
Let ABCD be a square with each side equal to a, then
(i) Perimeter = 4a
(ii) Area = ${\mathrm{a}}^2$
(iii) Diagonal = 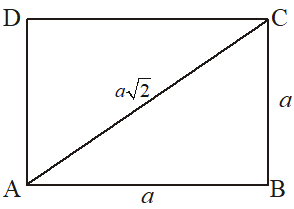$\mathrm{a}\sqrt{2}$

(iv) Area =$\frac{1}{2}{\left(\mathrm{diagonal}\right)}^2$
(v) Side of square = $\sqrt{\mathrm{Area}}=\frac{\mathrm{Perimeter}}{4}$
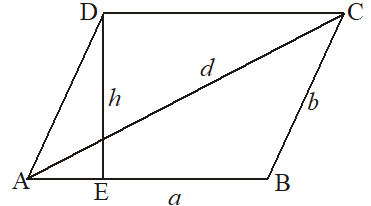
3. Parallelogram
Let a parallelogram ABCD with adjacent sides a and b with diagonal d.

Let $\mathrm{DE}\perp \mathrm{AB}$and DE = h, then
(i) perimeter = 2 (sum of adjacent sides)
= 2 (a + b)
(ii) area = base × height = a × h
(iii) if s = ,$\frac{\mathrm{a}+\mathrm{b}+\mathrm{d}}{2}$ then
area of parallelogram = $2\sqrt{\mathrm{s}(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{d})}$

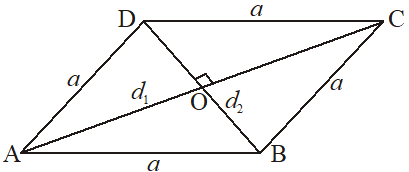
4. Rhombus
Let ABCD be a rhombus with each side equal to a. Let $d_1$ and $d_2$ are diagonals, then
(i) Area = $\frac{1}{2}\times {\mathrm{d}}_1\times {\mathrm{d}}_2$
(ii) Perimeter = $\frac{1}{2}\sqrt{{\mathrm{d}}_1^2+{\mathrm{d}}_2^2}$

(iii) Each side = $\frac{1}{2}\sqrt{{\mathrm{d}}_1^2+{\mathrm{d}}_2^2}$

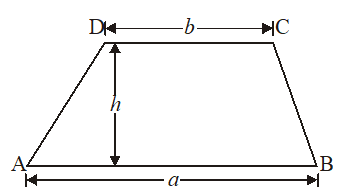
5 Trapezium

Let ABCD be a trapezium in which AB || DC such that AB = a and CD = b then, area of trapezium
= $\frac{1}{2}$ (sum of parallel sides) × (distance between them)

$=\frac{1}{2}(\mathrm{a}+\mathrm{b})\times \mathrm{h}$
6. Quadrilaterals
(i) Let ABCD be a quadrilateral in which length of diagonals = AC = d

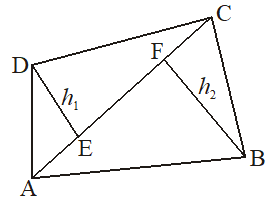
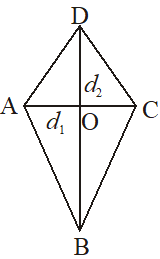
Let $\mathrm{DE}\perp \mathrm{AC}$ and $\mathrm{BF}\perp \mathrm{AC}$ such that DE = ${\mathrm{h}}_1$ and BF = ${\mathrm{h}}_2$ So, area of quadrilateral = $\frac{1}{2}\times \mathrm{d}\times \left({\mathrm{h}}_1+{\mathrm{h}}_2\right)$

(ii) Let ABCD be a kite then diagonals AC and BE are mutually perpendicular.
Let AC = ${\mathrm{d}}_1$ and BD = ${\mathrm{d}}_2$.
Area of kite =$\frac{1}{2}$ (product of the diagonals)
= $\frac{1}{2}\times {\mathrm{d}}_1\times {\mathrm{d}}_2$

(iii) Let ABCD be a cyclic quadrilateral with sides a, b, c and d, then,area of cyclic quadrilateral
= $\sqrt{(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})(\mathrm{s}–\mathrm{d})}$,
where  $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}}{2}$

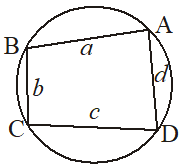
Example 4
In given figure, OABC is a rhombus whose three vertices lie on a circle and the forth vertex is O which is centre of the circle. If the area of rhombus is , find the radius of the circle.
Solution
Given, a circle with centre O and rhombus OABC, then
OA = AB = BC = OC
If radius of the circle is r then
OA = OB = r
$\therefore$OA = OB = AB = r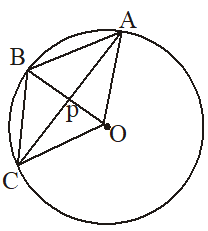

Hence $\mathrm{\Delta OAB}$ is an equilateral triangle.
$\therefore$ area of rhombus OABC = 2 (area of $\mathrm{\Delta OAB}$)
$\Rightarrow 72\sqrt{3}=2\times \frac{\sqrt{3}}{4}\times {\mathrm{r}}^2$
$\Rightarrow {\mathrm{r}}^2=144$
$\Rightarrow$r = 12 cm.
Example 5
A trapezium with its parallel sides in the ratio 15:4 is cut off from a rectangle whose sides measure 114m and 8m respectively. The area of trapezium is  $\frac{5}{12}$ of the area of the rectangle. Find the lengths of the parallel sides of the trapezium.
Solution
Let ABCD be a rectangle whose sides measure 114 m and 8 m and let PQRS is the trapezium which is cut of from rectangle ABCD such that its parallel sides PQ and RS are in the ratio 15:4.
Let PQ = 15x and RS = 4x
Now it is given that,
Area of trapezium PQRS
$=\frac{5}{12}\times (\mathrm{Area} \mathrm{of} rectangle\mathrm{ABCD})$

$\Rightarrow \frac{1}{2}(\mathrm{PQ}+\mathrm{RS})\times \mathrm{BC}=\frac{5}{12}\times \mathrm{AB}\times \mathrm{BC}$

$\Rightarrow \frac{1}{2}(15\mathrm{x}\times 4\mathrm{x})\times 8=\frac{5}{12}\times 144\times 8$

$\Rightarrow \frac{1}{2}\times 19\mathrm{x}=\frac{5}{2}\times 19\Rightarrow \mathrm{x}=5 \mathrm{cm}$
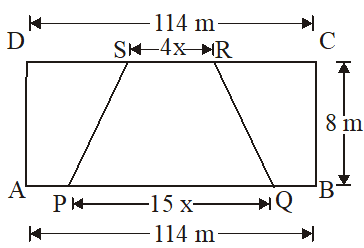
$\therefore \mathrm{PQ}=15\mathrm{x}=15\times 5=75 \mathrm{cm}$ and
RS = 4 x = 4 × 5 = 20 cm
Hence, parallel sides of trapezium are of lengths 75 cm and 20 cm.
Example 6
Find the area of a cyclic quadrilateral ABCD in which
AB = 10 cm, BC = 8 cm,
CD = 5 cm & DA = 7 cm.
Solution
Given a cyclic quadrilateral with sides a = 10 cm, b = 8 cm, c = 5 cm, d = 7 cm
$\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}}{2}=\frac{10+8+5+7}{2}=\frac{30}{2}=15 \mathrm{cm}$
Now, area of cyclic quadrilateral ABCD
$=\sqrt{(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})(\mathrm{s}–\mathrm{d})}$

$=\sqrt{(15–10)(15–8)(15–5)(15–7)}=\sqrt{5\times 7\times 10\times 8}$

$=\sqrt{5\times 5\times 2\times 2\times 2\times 2\times 7}$
= $20\sqrt{7} {\mathrm{cm}}^2$ = 20 × 2.645 $c{m}^2$ = 52.91 ${\mathrm{cm}}^2$
Area of given cyclic quadrilateral is 52.91 ${\mathrm{cm}}^2$.
Example 7
The diagonals of a rhombus are 112 cm and 66 cm. Find the length of a side and hence find the area of the rhombus, also find the perimeter of the rhombus.
Solution
Let ABCD be the rhombus whose each side is equal to a and with diagonal
AC = 112 cm and BD = 66 cm
Which intersect each other at point O. Since diagonals of a rhombus bisect each other at right angle.
$\therefore$OA = 56 cm, OB = 33 cm and $\angle \mathrm{AOB}=90°$.
In right triangle OAB by pythagoras theorem.
${\mathrm{AB}}^2={\mathrm{OA}}^2+{\mathrm{OB}}^2$
$\Rightarrow {\mathrm{a}}^2=(56{)}^2+(33{)}^2$
$\Rightarrow {\mathrm{a}}^2=3136+1089$
$\Rightarrow {\mathrm{a}}^2=4225$
$\Rightarrow$a = 65 cm
Hence, perimeter of rhombus

$\mathrm{ABCD}=4\mathrm{a}=4\times 65=260 \mathrm{cm}$

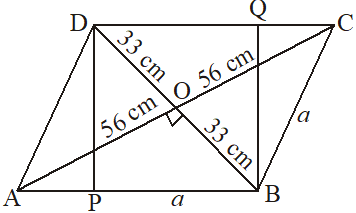
Area of rhombus ABCD =$\frac{1}{2}{ \mathrm{d}}_1{ \mathrm{d}}_2=\frac{1}{2}\times 112\times 66$
= 3969 ${\mathrm{cm}}^2$.
KEY POINTS
$\square$ Perimeter of right angled triangle = sum of sides Area of right angled triangle = $\frac{1}{2}$ × Base × Height
$\square$ Perimeter of isosceles triangle = sum of sides Area of isosceles triangle = $\frac{1}{2}$× Base × Height
$\square$ Perimeter of equilateral triangle = 3 × sides

Altitude of equilateral triangle = $\frac{\sqrt{3}}{2}\mathrm{a}$

Area of equilateral triangle = $\frac{\sqrt{3}}{4}{\mathrm{a}}^2$
$\square$ Heron’s formula:

Area of the triangle = $\sqrt{\mathrm{s}(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})}$ where, $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$
$\square$Perimeter of rectangle = 2 (l + b)

Area of rectangle = l × b

Diagonal of rectangle = $\sqrt{l^2+{\mathrm{b}}^2}$
$\square$Perimeter of square = 4a

Area of square = ${\mathrm{a}}^2$$=\frac{1}{2}$${\left(\mathrm{diag}\mathrm{onal}\right)}^2$

Diagonal of square = $\mathrm{a}\sqrt{2}$

Side of square = $\sqrt{\mathrm{Area}}=\frac{\mathrm{Perimeter}}{4}$
$\square$Perimeter of Parallelogram = 2 (sum of adjacent sides)

Area of Parallelogram = Base × Height
$\square$Area of Rhombus = $\frac{1}{2}\times {\mathrm{d}}_1\times {\mathrm{d}}_2$

Perimeter of Rhombus = $\frac{1}{2}$ $\sqrt{{\mathrm{d}}_1^2+{\mathrm{d}}_2^2}$.

Each side of Rhombus = $\frac{1}{2}\sqrt{{\mathrm{d}}_1^2+{\mathrm{d}}_2^2}$
$\square$Area of trapezium = $\frac{1}{2}$(sum of parallel sides) × (distance between them)
$\square$Area of quadrilateral = $\frac{1}{2}\times \mathrm{d}\times \left({\mathrm{h}}_1+{\mathrm{h}}_2\right)$
$\square$Area of kite = $\frac{1}{2}$(product of the diagonals)
$\square$Area of cyclic quadrilateral $=\sqrt{(\mathrm{s}–\mathrm{a})(\mathrm{s}–\mathrm{b})(\mathrm{s}–\mathrm{c})(\mathrm{s}–\mathrm{d})}$
where s = $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}}{2}$