8.1 Introduction
This is where we start getting into the heart of what algebra is about, solving equations. Here, we will be looking specially at linear equations and their solutions. We will start off slow and solve equations that use only one property, to make sure you have the individual concepts down. Then, we will pick up, the pace and mix them up where you need to use several properties and steps to get the job done.
8.2 Recap of basic terms
Variable
A symbol which take various numerical values is known as a variable or a literal.
Any letter can be used to denote a variable.
Examples: x, y, z, etc.
Constant
A symbol having a fixed numerical value is called a constant.
Examples: 3, 10, 15, 2009, etc.
Coefficient
In the product of a variable and a constant, each is called the coefficient of the other.
Example: 3x
Here 3 is the numerical coefficient of x and x is variable coefficient of 3.
Terms
Several parts of an algebraic expression separated by + or – signs are called the terms of the expression.
A constant or a variable is also known as a term.
Examples: 3x, 4, y, 5y, – 3xyz etc.
Equation
A statement of equality of two algebraic expression.
Involving at least one variable, is called an “equation”.
Examples
1) 10x + 100 = 1000
2) 3 + 4x + 5 = 0
3) 2009 + 2008x + 2010 = 0
Degree of an equation
The height power of a variable in an equation is called degree of an equation.
Examples
Let us consider the above polynomials.
1) 10x + 100 = 1000; Degree = 1
2) 3 + 4x + 5 = 0; Degree = 2
3) 2008 + 2009x + 2010 = 0; Degree = 3
8.3 Linear equations
Based on degree the equation are of following type.
|
S.No |
Degree of an equation |
Name of equation |
|
1 |
1 |
Linear equation |
Note:
We have separate names for equations up to fourth degree.
If the degree of an equation is greater than 4 then the equation is called the respective degree equation
Examples:
is degree equation.
is degree equation.
Linear equation
An equation whose degree is one(1) is called a Linear equation. (or) First degree equation is called Linear equation.
Examples: 3x + 4 = 5; 7x – 8y = 9
8.4 Types of Linear equations
Basically linear equation are of following type.
1. Linear equation in one variable.
2. Linear equation in two variable.
I. Linear equation in one variable
Observe the degree and number of variables in the following equation. 2009 x – 2010 = 0.
What is the degree of the above equation ?
Degree is 1; How many variables are there ?
There is only one variable (or) such kind of equations are called Linear equations in one variable.
An equation which contains only one variable with degree 1 is called Linear equation in one variable or simple linear equation.
General form
General form of Linear equations is ax + b = 0, where .
Examples:
An activity
Let us consider a simple linear equation.
100x + 9 = 2009
Which of the following values of x makes LHS and RHS of the above equation is equal?
a) x = 5 b) x = 10 c) x = 15 d) x = 20
a) When x = 5
LHS = 100x + 9 = 100(5) + 9 = 509 RHS
b) When x = 10
LHS = 100x + 9 = 100(10) + 9 = 1009 RHS
c) When x = 15
LHS = 100x + 9 = 100(15) + 9 = 1509 RHS
d) When x = 20
LHS = 100x + 19 = 100(20) + 9 = 2000+9 = 2009 = RHS.
Thus, when x = 20 LHS and RHS parts of the above equation are equal.
Such value of the variable is called solution of the equation.
Solution of the equation
The value of a variable for which either sides of the equation becomes equal is said to be solution of the equation
Examples: 2(x – 4) = 6 x = 7
3x – 2 = 5 – 4x x = 1
I. Linear equation in two variables
An equation contains two variables with degree 1 is called linear equations in two variable
General form
General form of Linear equation in two variables is ax + by + c = 0 or ax + by = c
Where a, b, c are real numbers x, y are variables and .
Examples
2x + 3y = – 6 ; 5x – 7y = – 9;
10x + 100y = 1000
8.5 Methods to solve simultaneous equations
Basically there are four methods to solve simultaneous Linear equations. They are
1) Elimination by substitution
2) Elimination by equating the co-efficient
3) Cross multiplication
4) Graphical method.
I. Elimination by substitution method
Let us understand the method by considering an example
Solve: x + y = 7 __________ (1)
–2x – 3y = 11 __________ (2)
Step -1 : Make any one variable as a subject (randomly) from any one of the two given equation.
Consider equation (1) and make y as a subject x + y = 7; y = 7 – x
Step- 2 : Substitute this value in the other equation to make it a linear equation in one variable and get the one of the variable value
Substitute this value of y in equation (2), we get :
2x – 3y = 11; 2x – 3(7 – x) = 11 ; 2x – 31 + 3x = 11
5x = 11 + 21;
Step-3 : Substitute this value in any one of the given equations and get the value of the other variable.
Substitute x = 32/5 in (1), we get :
x + y = 7; ; ; ;
The required solution is
I. Elimination by Equating the coefficients
Let us understand the method by considering an example.
11x – 5y = – 61 _______ (1)
3x – 20y = 2 _______ (2)
Step- 1: Multiply the given equations by suitable non-zero constants so as to make the coefficients of any one of the two variables same in both – the equation
Multiplying equation (1) by 3 and equation (2) by 11, we get:
33x – 15y + 183 = 0 _______ (4)
33x – 220y – 22 = 0 ______ (5)
Step-2: Add (or subtract) to eliminate the variable having some coefficient and obtain one of the variable value.
(3) – (4)
y = – 1
Step – 3: Substitute this value in any one of the given equations and get the value of the other variable:
Substitute y = – 1 in (1), we get:
11x – 5y + 61 = 0
11x – 5(– 1) + 61 = 0
11x + 5 + 61 = 0
11x + 66 = 0
x = – 6
The required solution is x = – 6 and y = – 1
II. Cross multiplication method
Let us understand the method by considering an example
2x + 3y – 4 = 0 ____________ (1)
3x + 2y – 11 = 0 ____________ (2)
Step – 1:
Step –2:
x = – 5; y = – 2
The required solution is x = – 5 and y = – 2
Example
Solve:
4x + 5y + 2 = 0 ____________ (1)
3x + y + 7 = 0 ____________ (2)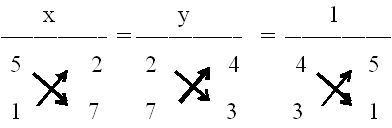
The required solutions is x = – 3 and y = 2
Graphical method
Let us understand the steps by taking an example.
Consider two simultaneous Linear equations.
4x + 3y – 7 = 0 ____________ (1)
2x – 3y + 1 = 0 ____________ (2)
Step 1: Consider two equations and make y as a subject in both the equations.
4x + 3y – 7 = 0
3y = 7 – 4x
2x – 3y + 1 = 0
3y = 2x + 1
_______ (4)
_______ (5)
Step 2: Substitute some at least 5 values of x in (4), (5) and obtain the corresponding values of y.
|
x |
0 |
1 |
2 |
||
|
5 |
3.6 |
2.3 |
1 |
|
x |
0 |
1 |
2 |
||
|
0.3 |
1 |
1.3 |
Step 3: Make the two sets of ordered pairs by taking the corresponding values of x and y.
Set 1: (– 2 , 5), (– 1 , 3.6), (0 , 2.3), (1, 1), (2 , 0.3)
Set 2: (– 2 , –1), (– 1 , 0.3), (0 , 0.3), (1, 1), (2 , 1.6)
Step 4: Plot all the points of set –1 on the graph and join. These points by straight line and do the same for second set on the same graph.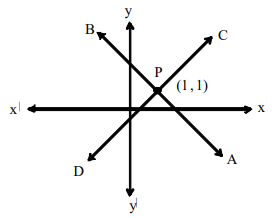
Step 5: The intersecting part of the two straight lines is the required solution.
The two lines are intersecting at (1, 1)
The required solution is x = 1, y = 1.
8.6 Solving of the system of Linear equations
Let us consider system of Linear equations
Case-1:
If Then
i) The system has unique solution
ii) Its graph is a pair of straight Lines intersecting at a unique point.
iii) These kind of equations are known as consistent independent.
Example :
Consider the system of equations
x + y – 3 = 0
2x + 5y – 12 = 0
The system has a unique solution.
Case -2:
If Then
i) The system has infinitely many solutions.
ii) The graph of the two equations are the same straight line (Coincident).
iii) System known as consistent independent.
Case – 3:
If Then
i) The system has no solution.
ii) The graph of the two equations are parallel lines.
iii) System is known as in – consistent.
8.7 Inequations
A statement of inequality between two algebraic expression involving at least one variable is called an in equation
Example
2x + 3x 100
x < – 32 + 3x
10x + 100 > 0.
2008x – 2009 x + 2.
Each of the above statements is an in equation.
8.8 Types of Inequations
Basically there are two types of inequations.
1. Absolute inequations
2. Conditional inequations
Absolute inequations
An inequation which is true for all values of variable is known as absolute inequation.
Example :
any variable raised to an even powers greater than zero.
Conditional inequation
An inequation which is true for all values of variable of the variable is known as conditional inequation.
Example
x + 9 > 20 it’s true when x > 11
2x – 10 < 90 true when x < 50
Linear inequation
First degree inequation is called Linear inequation
Example
x – 7 < 1 – 13
x + 27 > – 38
Solution set of the inequation
The set of values of variable which satisfy the given inequation is said to be the solution set of the inequation.
Example
4x – 90 > – 10 (x + N) x > 20
Solution set = {21, 22, 23, ……….}.
8.9 Properties of Linear Inequations
i) Adding or subtracting the same numbers to each side of an inequation does not change the inequality.
Example
Consider an inequation
x – 7 > 23 ________ (1)
x > 23 + 7
x > 30
Add 5 on both to inequation (1). We get
x – 7 + 5 > 23 + 5
x – 2 > 28
x > 28 + 2
x > 30
Add 5 on both to inequation (1)
x – 7 – 5 > 23 – 5
x – 12 > 18
x > 18 + 12
x > 30
In both cases the solution is same.
ii) Multiplying or dividing with the same negative number to each side of an inequaiton changes the inequality.
Example
Let us consider an inequation
3x – 11 > 10
2x > 10 + 11
2x > 21
x > 7.
Divide both sides of the inequation 3x – 11 > 10 by – 5
11 – 3x > – 10
– 3x > – 21
x < 7
Let us multiply
– 5 (3x – 11) > (– 5) × 10
– 15 x + 55 > – 50
– 15 x > – 105
x < 7
Example
Let us consider an inequation – 12 > – 8
Multiply by both sides of the inequation – 4.
(– 12) × (– 4) < (– 8) × (– 4)
48 < 32
But the above statement is false as 48 is not less than 32
To make the above statement true we have to reverse the inequality.
i.e., 48 < 32 changing to 48 > 32
– 12 < – 8
Divide both sides of inequation by (–4).
3 < 2
But the above statement is false as 3 is not less than 2
To make the above statement true we have to reverse the inequation.
i.e., 3 < 2 change to 3 > 2








