Surface Areas and Volumes

13.1. INTRODUCTION
Mensuration is the art of measuring. It is a branch of mathematics with measurement of length, areas and volumes of plane and solid figures.
Solid
A physical body that occupies some space is called a solid. It has three dimensions in space called length, breadth and height.
Example : a pen, a match box, a room etc.
Volume
The space occupied by a solid body is called its volume. Cubic centimeters (cm³) and cubic meters (m³) are the common units of volume.
13.2. CUBOID OR RECTANGULAR PARALLELEPIPED
It is a solid with six rectangular faces. If length, breadth and height of a cuboid are l, b and h respectively then,
(i) Volume of cuboid = l × b × h
= area of base × height cu. units
(ii) Total surface area of
cuboid = 2 (lb + bh + hl) sq. units
(iii) Curved surface area of cuboid or surface
area of 4 walls = 2 (l + b) × h sq. units
(iv) Diagonal of cuboid =  $\sqrt{l^2+{\mathrm{b}}^2+{\mathrm{h}}^2}$ units
(v) Height of cuboid =  $\frac{\mathrm{Volume}}{\mathrm{base} \mathrm{area}}$ units

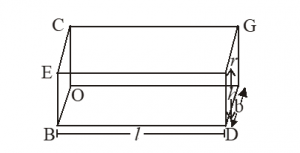
(vi) Area of base = $\frac{\mathrm{volume}}{\mathrm{height}}$ sq. units
(vii) Surface area of cuboid, in which top face is open = lb + 2 (bh + hl) sq. units
(viii) Diagonals of faces of cuboid = $\sqrt{l^2+{\mathrm{b}}^2},\sqrt{{\mathrm{b}}^2+{\mathrm{h}}^2},\sqrt{{\mathrm{h}}^2+l^2}$ units
(ix) Perimeter of the cuboid = 4(l + b + h) units
13.3. CUBE
Cube is a rectangular solid. It has six faces in which every face is a square. Let each edge of a cube measures ‘a’ then

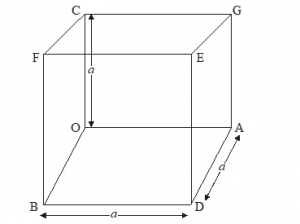
(i) Volume of a cube = a³ cu. units
(ii) Total surface area of cube = 6a² sq. units
(iii) Curved surface area of cube = 4a² sq. units
(iv) Diagonal of cube =  $a\sqrt{3}$ units
(v) Edge of cube = (volume)^1/3 units
(vi) Diagonal of face of the cube = $a\sqrt{2}$ units
(vii) Perimeter of the cube = 12a units.
LEARN IT
(i) Cuboid has six faces, eight vertices and twelve edges. Each face of a cuboid is a rectangle. 
(ii) Cube is a cuboid whose each face is a square.
13.4. RIGHT CIRCULAR CYLINDER
A solid generated by the revolution of a rectangle about one of its sides is called a right circular cylinder. In given figure OA is called the axis of the cylinder. Let

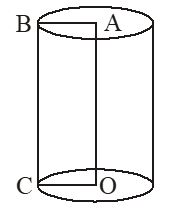
OA = height of the cylinder = h and
AB = OC = radius of the base of the cylinder = r
then we have
(i) Area of the base of a right circular cylinder =  $\mathrm{\pi }$r² sq. units
(ii) Area of the curved surface of a right circular cylinder
= Circumference of the base × Height = 2$\mathrm{\pi }$rh sq. units
(iii) Total surface area of a right circular cylinder
= Area of curved surface + 2 × Base area
= $(2\mathrm{\pi rh}+2{\mathrm{\pi r}}^2)$ sq. units = $2\mathrm{\pi r}(\mathrm{r}+\mathrm{h})$ sq. units
(iv) Volume of a right circular cylinder = Area of base × height
= $\left({\mathrm{\pi r}}^2\right)\times \mathrm{h}$ cu. units = ${\mathrm{\pi r}}^2\mathrm{h}$ cu. units
Note : If in given figure OA is not perpendicular to OC i..e if the line joining the centres of circular ends of a cylinder is not perpendicular to the circular ends then the cylinder is not a right circular cylinder.
13.5. HOLLOW CYLINDER
A hollow cylinder is a solid bounded by two coaxial cylinders of the same height and different radii. If R and r be the external and internal radii of a hollow cylinder and h be its height, then

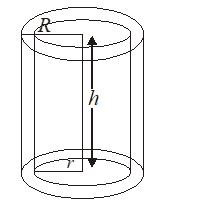
(i) Each base surface area = $\mathrm{\pi }({\mathrm{R}}^2–{\mathrm{r}}^2)$ sq. units
(ii) Curved surface area = (External surface area) + (Internal surface area)
$= 2\mathrm{\pi Rh} + 2\mathrm{\pi rh} = 2\mathrm{\pi h}(\mathrm{R}+\mathrm{r})$
(iii) Total surface area = (External surface area) + (Internal surface area) + 2 (base area)
$=2\mathrm{\pi Rh} + 2\mathrm{\pi rh} +2\mathrm{\pi }({\mathrm{R}}^2–{\mathrm{r}}^2)$
$=2\mathrm{\pi h}(\mathrm{R}+\mathrm{r}) +2\mathrm{\pi } (\mathrm{R}+\mathrm{r})(\mathrm{R}–\mathrm{r}) = 2\mathrm{\pi }(\mathrm{R}+\mathrm{r})(\mathrm{h}+\mathrm{R}–\mathrm{r})$ sq. units
(iv) Volume of the material
= Exterior volume – interior volume = ${\mathrm{\pi R}}^2\mathrm{h}–{\mathrm{\pi r}}^2\mathrm{h} = \mathrm{\pi h}({\mathrm{R}}^2–{\mathrm{r}}^2)$.
13.6. RIGHT CIRCULAR CONE
If a right angled triangle is revolved about one of the sides containing a right angle, the solid thus formed is called a right circular cone.

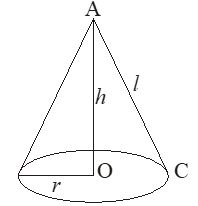
A right circular cone can be also defined as a solid generated by revolving a line segment which passes through a fixed point and which makes a constant angle with a fixed line. In given figure we have,
The fixed point A is called vertex of the cone.
The fixed line AO is called the axis of the cone.
The base of a right circular cone is in circular shape such that the line joining vertex to the center of the circle is perpendicular to the base.
The length of the line segment joining the vertex to any point on the circular edge of the base is called the slant height of the cone.
Let Height of the cone = OA = h
Radius of the base of the cone = OB = r
and slant height of the cone = AC = l  then we have
(i) Slant height = l = $\sqrt{r^2+h^2}$ units
(ii) Area of base = $\mathrm{\pi }$r² sq. units
(iii) Volume = 1/3 (Area of base) × Height = $\frac{1}{3}{\mathrm{\pi r}}^2\mathrm{h}$ cu units
(iv) Curved surface area= $\mathrm{\pi r}l$ sq. units
(v) Total surface area = Area of circular base + curved surface area = $({\mathrm{\pi r}}^2+\mathrm{\pi r}l)$ sq. units = $\mathrm{\pi r}(\mathrm{r}+l)$ sq. units
Note : If the base of a cone is not circular or if the line joining the vertex to the centre of the base is not perpendicular to the base then the cone is not right circular cone.
13.7. SPHERE
If a circle is revolved about its one of the diameter, then the solid formed is a sphere. A sphere can be described as a set of all those points in space, which are equidistant from a fixed point.
The fixed point is called the centre of the sphere and the constant distance between the centre and any point on the sphere is called radius of the sphere.
Let the radius of the sphere be r, then
(i) volume of the sphere = $\frac{4}{3}{\mathrm{\pi r}}^3$ cu. units

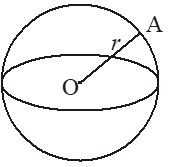
(ii) surface area of  the sphere = $4{\mathrm{\pi r}}^2$ sq. units
13.8. HEMISPHERE
A plane passing through the centre of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
Let the radius of the hemisphere be r, then
(i) Volume of the hemisphere = $\frac{2}{3}{\mathrm{\pi r}}^3$ cu. units
(ii) curved surface area = $2{\mathrm{\pi r}}^2$ sq. units

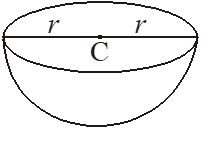
(ii) Total surface area = $3{\mathrm{\pi r}}^2$ sq. units
13.9. SPHERICAL SHELL
The difference of two solid concentric spheres is called a spherical shell.
Let the outer radius and inner radius of a spherical shell are R and r respectively, then
(i) Volume of spherical shell = $\frac{4}{3}\mathrm{\pi }({\mathrm{R}}^3–{\mathrm{r}}^3)$ cube units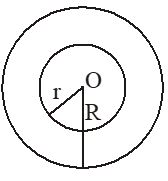

(ii) External surface area = $4{\mathrm{\pi R}}^2$ sq. units
(iii) Internal surface area = $4{\mathrm{\pi r}}^2$  sq. units