1.1 Introduction
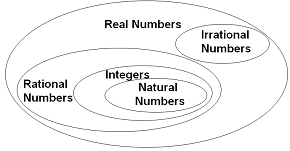
A number is a mathematical object used in counting and measuring. A notational symbol which represents a number is called a numeral. In addition to their use in counting and measuring, numerals are often used for labels (telephone numbers), for ordering (serial numbers), and for codes (ISBNs). In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers and complex numbers.
Certain procedures which take one or more numbers as input and produce a number as output are called numerical operations. Unitary operations take a single input number and produce a single output number. For example, the successor operation adds one to an integer, thus the successor of 4 is 5. More common are binary operations which take two input numbers and produce a single output number. Examples of binary operations include addition, subtraction, multiplication, division and exponentiation. The study of numerical operations is called arithmetic.
1.2 Review of Basic Numbers
Natural Numbers
The countable numbers like 1, 2, 3… …….. are called Natural Numbers.
The set of natural numbers is denoted by N. N = { 1, 2, 3, 4…….}
Whole Numbers
The numbers containing natural numbers and zero are called Whole Numbers.
The set of whole numbers is denoted by W.
W = { 0, 1, 2, 3, 4, …………}
Integers
The set of numbers containing negatives of natural numbers along with whole numbers is called Integers.
The set of integers is denoted by Z.
Z = { …….–3, –2, –1, 0, 1, 2, 3 …….}
1.3 Rational and Irrational Numbers
Rational Numbers
The numbers of the form p/q where p and q are integers and , are called Rational Numbers.
Rational Numbers are denoted by Q.
Example:
Note:
i) Zero is also a rational number, since
ii) Every integer is also a rational number, since any integer can be expressed as .
For example, and 5 is a rational number.
Equivalent rational numbers
If is a rational number and m is any non-zero integer, then .
In this case, and are called Equivalent rational numbers.
Example: A rational number on multiplying both numerator and denominator with 5 , we get .
Here, and are called Equivalent rational numbers.
Irrational Numbers
Any number that cannot be expressed in the form of (which is neither terminating nor repeating decimal) is said to be an irrational number.
Example:
Why is an irrational number?
The value of . The close observation of the value shows that it is a non-repeating and non-terminating decimal. Further, it cannot be expressed in the form of . Hence, it is an irrational number.
Is rational or irrational number?
The approximate value of is , which is equal to 3.142857143…
is irrational number.
Properties of Rational and Irrational Numbers
|
Properties |
Rational |
Irrational |
Rational & Irrational |
|
Addition |
The sum of two rational numbers is a rational number. |
The sum of two irrational numbers may or may not result in an irrational number. |
The sum of a rational and an irrational number is an irrational number. |
|
Subtraction |
The difference of two |
The difference of two irrational numbers may or may not result in an irrational number. |
The difference of a rational and an irrational number is an irrational number. |
|
Multiplication |
The product of two |
The product of two irrational numbers may or may not result in an irrational number. |
The product of a rational and an irrational number is an irrational number. |
|
Division |
The quotient of two |
The quotient of two irrational numbers may or may not result in an irrational number. |
The quotient of a rational and an irrational number is an irrational number. |
Difference Between Rational and Irrational Numbers
|
Rational Numbers |
Irrational Numbers |
|
1. Rational numbers can be expressed in the form of p/q |
1. Irrational numbers cannot be expressed in the form of p/q |
Finding the rational numbers between two rationals
Mid value method: If r and s be rational numbers then is between r and s.
[If r < s then ]
Example: Find a rational number between 3 and 4.
Solution: We know that is between r and s.
Therefore, a rational number between 3 and 4 is
Hence,(= 3.5) is a rational number between 3 and 4.
Finding Out Irrational Numbers between Any Two Rational Numbers
We know that between any two rational numbers, there is an infinite number of rational numbers; and between any two irrational numbers, there is again an infinite number of irrational numbers.
How can we find an irrational number between two rational numbers?
To find irrational numbers between rational numbers, we follow two steps.
Step 1
Find the decimal representation (up to 2 or 3 places of decimal) of the two rational numbers. Let those decimal representations be a and b and let a < b.
Step 2
Choose the required non-repetitive and non-terminating decimal numbers between a and b. That decimal number will be the required irrational number.
Let us discuss a few more examples.
Example: Find an irrational number between 0.12 and 0.15.
Solution: The rational numbers are already in the decimal form.
Let a = 0.12 and b = 0.15.
We can see that a < b.
There are infinite number of irrational numbers between a and b.
Clearly, the number 0.12101001000 … lies between 0.12 and 0.15.
Hence, the required irrational number between 0.12 and 0.15 is 0.12101001000 …
Example: Find 5 irrational numbers between and .
Solution:
Step 1:The decimal expansion of is 0.3333…
The decimal expansion of is 0.4 or 0.400.
We can see that 0.333 < 0.4.
Step 2: Hence, the 5 irrational numbers between 0.33 and 0.4 are
0.34560561562563…
0.3574744744474444…
0.369874562301…
0.3710110111011110…
0.39919293…
In this way, we can find any number of irrational numbers between any two given rational numbers.
1.4 Real Numbers
Real numbers are the union of rational and irrational numbers.
1.5 Even and Odd Numbers
Even Numbers
The numbers that are divisible by 2 are called even numbers(E).
The general notation of an even number is 2n where .
Example: 2, 4, 6 …………. are all even numbers.
also –2, –4, –6 …………… are even numbers.
Odd Numbers
The integers that are not exactly divisible by 2 are called odd numbers.
The general notation of an odd number is 2n+1 where .
Example: 1, 3, 5 …………….are odd numbers.
Note: Every odd number is obtained by adding 1 to every even number.
Example: 2 + 1 = 3, 4 + 1 = 5
Properties of even and odd numbers
|
Even Number |
Odd Number |
|
The sum or difference of two even numbers is even. |
The sum or difference of two odd numbers is even. |
|
The square of an even number is even. |
The square of an odd number is odd. |
|
The sum of squares of two even numbers is even. |
The sum of squares of two odd numbers is even. |
|
The product of two even numbers is even. |
The product of two odd numbers is odd. |
|
The square root of an even perfect square is an even number. |
The square root of an odd perfect square is an odd number. |
|
i) The sum or difference of an even numbers and an odd number is odd. |
|
1.6 Representing rational and irrational numbers on the number line
We known that all the number (either rational or irrational) can be represented on number line.
Example
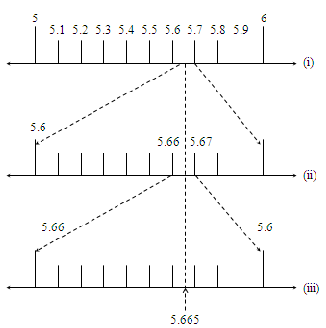
(i) Visualize the position of 5.665 on the number line, through, successive magnification
(ii) Represent on the real number line
Solution:
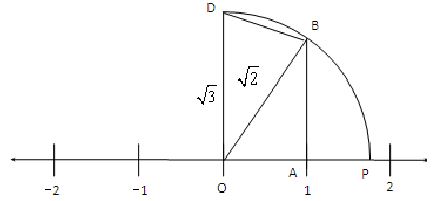
on base OA = 1 unit of length, braw ABOA and cut off AB = 1 unit join OB.
Then
Draw BD OB and cut off BD = 1 unit.
Then
Cut off OP = OD =
Prepresents the real number (irrational)
1.7 Operations on Irrational Numbers
We have already learnt how to perform operations such as addition, subtraction, multiplication, and division on rational numbers, integers, decimals, etc. Performing these operations on irrational numbers is also possible. However, before learning to perform operations on irrational numbers, we first need to know the concept of like and unlike terms.
Let us learn what ‘like’ and ‘unlike’ terms are.
Like Terms
The terms (single terms) whose irrational parts are the same are known as like terms.
For example, are like terms because the irrational part of both these numbers is .
Unlike Terms
The terms whose irrational parts are not the same are known as unlike terms.
For example, are unlike terms because the irrational parts of both these numbers are different .
Remember
Only like terms can be added or subtracted in the operations of irrational numbers.
Let us understand this concept with the help of a few examples.
Example : Add
Solution:
(collecting like terms)
Example : Multiply with .
Solution:
Example : Simplify the expression
Solution:
Example : Divide by .
Solution:
Example : Prove that .
Solution: We have to prove that
Left hand side =
Right hand side
Hence, L.H.S = R.H.S
Hence,
1.8 Rationalization
Changing an irrational number in to a rational number is called “rationalization” and the factor by number is called “rationalizing factor”
R.F. of
R.F. of
R.F. of
R.F. of
R.F. of
R.F. of
Example : (i) Rationalize:
(ii) Simplify
Solution : (i)
(multiplied and divisible by conjugate)
(ii)
Same condition =
1.9 Some Important Identities related to square roots
Let x and y be positive real numbers, then
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Example
(i) Simplify
(ii) Simplify
Solution
(i)
(ii)
1.10 Laws of exponents for real numbers
Example:(i) Which is greater (or)
(ii) Simplify
Solution
(i) LCM of 2 and 3 = 6
as , we have
1.11 Prime numbers & Composite numbers
Prime Numbers
A number which has exactly two different factors one and itself is called a prime number.
Example: 2, 3, 5, 7, 11,13, 17, 19 etc.
We can write 2 = 2 × 1.There are two factors of 2. They are 2 and 1. Now we can say that 2 is divisible by 2 and 1, i.e., 2 is divisible by itself and 1, and similarly 3 = 3×1, 5 = 5 ×1.
Composite Numbers
The natural numbers other than 1 and primes are called composite numbers.
Note: The Composite numbers have a minimum of three factors.
Example: The factors of 4 are 1, 2, 4 and the factors of 6 are 1, 2, 3 and 6.
Points to remember
i) Every prime number has two factors.
ii) Every composite number has at least three factors.
iii) 1 is neither a prime nor a composite number.
iv) 2 is the only even prime number.
Types of Primes
Twin Primes
The two prime numbers whose difference is 2 are called Twin Primes.
Example:
(i) 3, 5
(ii) 5, 7
(iii) 11, 13
Prime triplets
Three consecutive odd primes are known as prime triplets.
Example: 3, 5, 7 (One and only prime triplet )
Factor and Multiple
If b divides a and leaves zero as remainder, then b is called a factor or divisor of a and a is called the multiple of b.
Example: 5 divides 20 leaving remainder 0.
Hence 5 is the factor or divisor of 20 and 20 is called the multiple of 5.
Therefore, 20 = 5 × 4, where 4 is the other factor of 20.
Note: Suppose a natural number n is expressed as n = then the number of divisors or factors of n is given by
n = (a +1) (b +1) (c +1)…
Prime factors
If the factors of the given number are prime numbers, then such factors are called prime factors.
Example: Consider the number 36.
36 = 4 × 9 = 2 × 2 × 3 × 3 = ×
Therefore, the prime factors of 36 are 2 and 3.
Prime Factorization
Expressing the given number as a product of prime factors is called prime factorization.
Example: What are the prime factors of 12?
It is best to start working from the smallest prime number, which is 2, so let’s check
12 ÷ 2 = 6
But 6 is not a prime number, so we need to factor it further
6 ÷ 2 = 3
And 3 is a prime number, so 12 = 2 × 2 × 3
As you can see, every factor is a prime number, so the answer must be right – the prime factorization of 12 is 2 × 2 × 3, which can also be written as × 3
Note: F (n) indicates factors of n and M(n) indicates multiples of n.
1.12 Fractions
A number of the form , where p, q are integers and is known as a fraction.
Example: etc.
Note: All fractions are rational numbers.
Difference between rational number and fraction
Rational numbers and fractions are of the form
Any integer is a rational number, since we can express any integer as But in a fraction, the denominator part should not be 1.
Types of Fractions
i) Simple Fraction: A fraction in its lowest terms is known as a simple fraction.
Example: etc.
ii) Proper fraction: A fraction in which numerator is less than denominator is known as a proper fraction.
Example: etc.
iii) Improper fraction: A fraction in which numerator is greater than denominator is known as an improper fraction.
Example: , etc.
iv) Mixed fraction: The fraction of the form , where is a proper fraction is known as a mixed fraction.
Example: , etc.
v) Compound fraction : A fraction whose one or both terms are fractions is called a compound fraction. Normal form of a compound fraction is .
Note: Finding of fraction in between any two fractions and is given by .
Example: Insert a fraction between and
The fraction which comes between and
vi) Like fractions: Fractions having the same denominators are called like fractions.
Example: , etc.
vii) Unlike fractions: Fractions having different denominators are called unlike fractions.
Example: , etc.
How to convert a given Improper fraction into a mixed fraction ?
In general, the mixed fraction of is : .
Where Q = Quotient R = Remainder
Now, let us find the mixed fraction of
Fraction between any two fractions
Finding of a fraction in between any two fractions and is given by the form
Equivalent Fractions
Some fractions may look different, but are really the same. If we multiply numerator and denominator with same number the fraction remains unchanged.
Example:
1.13 Decimals
The simplified form of a fraction is called a decimal.
How do we read a decimal?
Consider 123.456 .
Whole number part, 123, should be read as one hundred and twenty three.
The decimal point ‘’ should be read as point.
The decimal part 456 should be read as four, five, six.
Conversion of Decimals to Fractions
Let us express 0.75 as a fraction.
Step – 1: Count the numbers after the decimal point, let it be x, in 0.75 we have x = 2.
Step – 2 : Now multiply and divide numerator by . i.e. = 100.
0.75 =
Step – 3 : Reduce the above fraction to simplest form .
Note: When we multiply a decimal number with 100, the decimal point moves 2 places right. When we divide it with 100, the decimal point moves 2 places left.
Example : Express 331.570063 as a fraction.
we have 6 digits after the decimal point.
Decimal values of some fractions
|
Fraction |
Value |
|
0.1 |
|
|
0.3 |
|
|
1.3 |
|
|
70.5 |
|
Fraction |
Value |
|
0.01 |
|
|
0.03 |
|
|
0.13 |
|
|
7.05 |
|
Fraction |
Value |
|
0.2 |
|
|
0.5 |
|
|
0.15 |
|
|
1.08 |
Conversion of Fractions to Decimals
Let us understand the steps by expressing in decimal.
Step – 1: Write the numerator as it is 17153
Step – 2: Count the number of zeros in the denominator.
Let it be x. Here x = 3
Step – 3: From ‘right to left’ in the numerator keep the decimal point after x places.
Classification of decimals
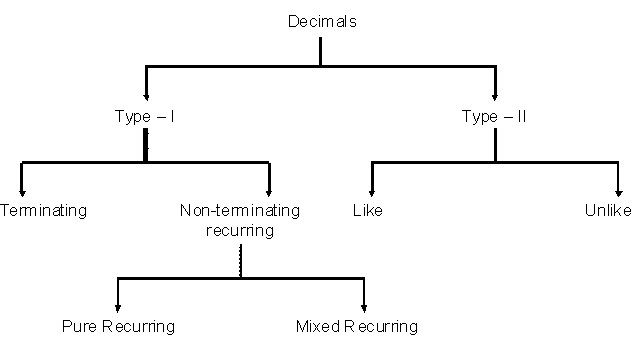
Terminating Decimal
The decimal in which the digits end after the decimal point.
Example: 0.25, 0.5, 0.75, etc.
Non-terminating Decimal
The decimal in which the digits do not end after the decimal point.
Example: 1.762586 …., , , , etc.
Note: The non-terminating decimals can be recurring or non-recurring. The non-terminating recurring decimals are again classified into pure recurring and mixed recurring.
Pure recurring Decimals
These are the decimals in which the set of digits is repeated immediately after the decimal point.
Example:
Mixed recurring Decimals
These are the decimals in which the set of digits is not repeated immediately after the decimal point.
Example:
Conversion of a pure recurring decimal into a fraction
Write the repeated figures only once in the numerator and take as many nines in the denominator as is the number of repeating figures.
Thus, .
Conversion of a mixed recurring decimal into a fraction:
In the numerator, take the difference between the number formed by all the digits after decimal point (taking repeated digits only once) and that formed by the digits which are not repeated. In the denominator, take the number formed by as many nines as there are repeating digits followed by as many zeros as is the number of non-repeating digits.
Thus,
Types of Decimals
Based on number of decimal places in a set of decimals, they are classified into like and unlike decimals.
Like decimals
The decimal numbers that consists of same number of decimal places after decimal point are called like decimals.
For example, 3.54 , 13.68 , 0.47 are like decimals as they all have same number of decimal places i.e., two.
Unlike decimals
The decimal numbers that consists of different number of decimal places after decimal point are called unlike decimals.
For example, 3.54, 13.8, 0.475 are unlike decimals as they have different number of decimal places.
3.54 2 decimal places
13.8 1 decimal place
0.475 3 decimal places
Let’s convert 12.45 , 6.5 , 0.735 & 145.05 into a set of like decimals.
12.45 decimal places = 12.450
6.5 decimal place = 6.500
0.735 decimal places = 0.735
145.05 decimal places = 145.050
to make them like decimals we need same number of decimal places
12.450 , 6.500 , 0.735 , 145.050 is the set of like decimals.
Comparison of decimals
Let us understand the steps of comparison by the following example.
Arrange 0.85 , 1.58 , 2.85 , 0.58 , 0.583 in descending order.
Step – 1: Write the given decimals as the set of like decimals i.e. 0.850, 1.580, 2.850 , 0.580 , 0.583
Step – 2: Compare their integral parts
The decimal number with greater integral part is greater.
2.850 > 1.580 (0.850, 0.580, 0.583)
Step – 3: If the integral parts are same, then compare the first decimal place.
The number with greater first decimal place is greater.
0.850 > (0.580 and 0.583)
Step – 4: If the first decimal place are same, then compare the second decimal places
But they are also equal.
So, we compare the third decimal place. i.e. 0.580, 0.583
0 3 0.583 > 0.580
Number with greater third decimal place is greater.
2.85 > 1.58 > 0.85 > 0.583 > 0.58
Rounding off a Decimal
|
Various Cases |
Example |
|
Retain as many digits after the decimal point as are required and omit the remaining digits. |
|
|
In the set of omitted digits, if the first digit is 5, then increase the last retained digit by 1. |
Let’s round off 2.6457, to two decimal places. |
|
In the set of omitted digits, if the first digit is greater than 5, then increase the last retained digit by 1. |
Let’s round off 7.5689 to two decimal places. |
|
In the set of omitted digits, if the first digit is less than 5, then it remains unchanged. |
Let’s round off 5.12345 to three decimal places. |
1.14 L.C.M
Least Common Multiple
Least number that is divisible by all the given numbers is called Least Common Multiple.
For example, the common multiples of 7 and 2 are 14, 28, 42, etc,
Among these, 14 is least and is the LCM of 7 and 2.
Methods of finding LCM
Multiples Listing Method
In this method, LCM is found by listing several multiples of the given numbers. This method is generally used for finding LCM of numbers with less difference.
Example: Let us find the L.C.M of 3 and 5.
Multiples of 3 are
etc.,
Multiples of 5 are
etc.,
The common multiples of 3 and 5 are etc.
The Least Common Multiple of 3 and 5 is
Prime Factorization Method
In order to find the LCM of two or more given numbers we write the prime factorization of each of the given numbers. Then, the required LCM of these numbers is the product of all different prime factors of the numbers, now multiplying common prime factors having greater powers, will get L.C.M.
Example: Let us find the LCM of 108, 72and 360.
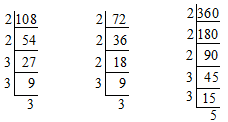
108 = ×; 72 = × ; 360 = × × 5
Now the factors are 108 = ×
72 = ×
360 = × × 5
Highest common prime factors = 5 = 1080
LCM of 108, 72 and 360 = 1080
Long Division Method
In order to find the LCM of any amount of numbers, we use the long this method.
i) We arrange the given numbers in a line, in any order.
ii) We divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible.
iii) This process is repeated till no two of the given numbers are divisible by the same number.
iv) The product of the divisors and the undivided numbers is the required LCM of the given numbers.
Example: Let’s find the LCM of 16, 8 and 4.
LCM of 16, 8 and 4 = 2 2 2 2 = 16
Note: We must take prime numbers as divisors like 2, 3, 5, 7…………
1.15 HCF
Highest Common Factor
The number that divides all the given numbers is called as a Common Factor. The greatest among the common factors of the given numbers is called Highest Common Factor (HCF).
Example: The common factors for 24 and 12 are 2, 4, 6, 12.
Among the factors, 12 is the highest and is the HCF of 24 and 12 .
HCF is also called as :
GCD – Greatest Common Divisor
HCD – Highest Common Divisor
GCF – Greatest Common Factor
HCF – Highest Common Factor
Methods of finding HCF
Listing the Factors Method
In this method, HCF is found by listing several factors of the given numbers.
Example: Let us find the HCF of 36 and 48.
Step – 1: Write down all the factors of the given numbers.
36 1, 2, 3, 4, 6, 9, 12, 18, 36.
48 1, 2, 3, 4, 6, 8, 12, 24, 48
Step – 2: Check the common factors of the given numbers. 1, 2, 3, 4, 6, 12
Step – 3: Identify the greatest among those common factors of the given numbers.
The greatest among these factors is 12 and is the HCF of the 36 and 48.
Prime factorization Method
We first find the prime factorization of each of the given numbers. Then the product of all common prime factors, using the least power of each common prime factor, is the HCF of the given numbers.
Example: Lets find the HCF of 200 and 320
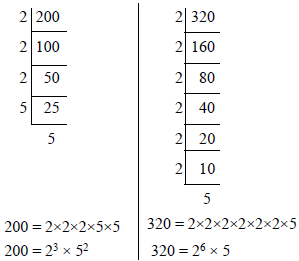
HCF = product of lowest power prime factors = × 5 = 40
Long Division Method
The following steps should be used to find the HCF by long division method.
i) If two numbers are given, divide the greater number by the smaller one.
ii) Divide the divisor by the remainder.
iii) Repeat the process of dividing the preceding divisor by the remainder last obtained, till the remainder zero is obtained.
iv) The last divisor is the required HCF of the given numbers.
Example: Let us find the HCF of 136, 170 and 255, using the long division method.
Sol: 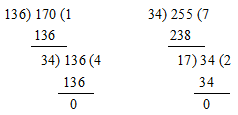
HCF of 136, 170 and 255 = 17
Solving methods to solve various types of problems related to HCF
Type – 1: Find the greatest number that will exactly divide a, b and c.
Approach:
Required number = HCF of a, b and c.
Type – 2 : Find the greatest number that will divide x, y and z leaving remainders a, b and c respectively.
Approach:
Required number = HCF of (x–a), (y–b) and (z–c)
Type – 3: Find the greatest number that will divide a, b and c leaving the same remainder in each case.
Approach:
Required number = HCF of (a–b), (b–c) and (c–a)
Example: Find the greatest number that will divide 148, 246 and 623 leaving remainders 4, 6 and 11 respectively.
Required number = HCF of (148–4), (246–6) and (623–11)
= HCF of 144, 240 and 612
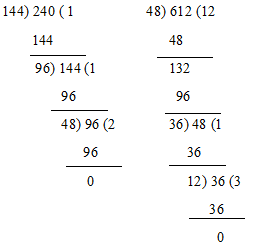
HCF of 144, 240 and 612 = 12
Required number = 12
Co-primes
The numbers that do not have any common factor other than 1 are called co-prime or relatively prime.
Example: Consider the numbers 8 and 15
Set of factors of 8 = {1, 2, 4, 8}
Set of factors of 15 = {1, 3, 5, 15}
The common factor of 8 and 15 is 1 only.
8, 15 are co-primes.
Note: Two numbers are said to be co-prime or relatively prime, if their HCF is 1.
For example, the HCF of 4, 13 is 1. Therefore, 4 and 13 are co-prime numbers..
1.16 HCF and LCM
HCF and LCM of Fractions
i) HCF of fractions =
ii) LCM of fractions =
Relation between LCM and HCF
Consider any two numbers a and b. Let their LCM and HCF be x and y respectively.
Then ab = xy
Note:








