Constructions

12.1. INTRODUCTION
In this chapter, we shall review some elementary constructions which we have already learnt in previous chapters. We will also construct some new accurate figures which are needed in the construction of different things.
For these constructions, we shall apply some already proved geometrical theorems. Following geometrical instruments are required for the construction of accurate figures :
(i) a graduated scale
(ii) a pair of set squares
(iii) a pair of divider
(iv) a pair of compass
(v) a protractor
12.2. BASIC CONSTRUCTIONS
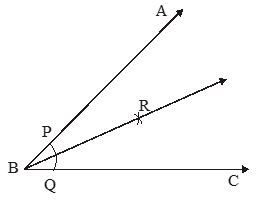
Construction 1
To construct the bisector of a given angle
A line which bisects a given angle is known as angle bisector of that angle. Let a given angle ABC. We want to construct its bisector.
Steps of Construction
(i) Take B as a centre and with any radius, we draw an arc intersecting arms BA and BC at P and Q respectively.
(ii) With P and Q as centres and with the radius more than $\frac{1}{2}\mathrm{PQ}$, we draw arcs, intersecting each other at point R.
(iii) We draw ray BR. Then ray BR is required angle bisector of ABC.

Construction 2
To construct perpendicular bisector of a given line segment
A line which is perpendicular to the given line segment and bisects it, is known as its perpendicular bisector. Let a given line segment AB, we have to draw perpendicular bisector of AB.

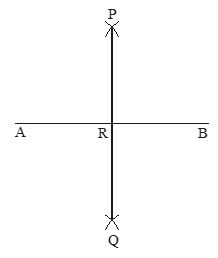
Steps of Construction
(i) For given line segment AB, we take A as a centre and with radius more than $\frac{1}{2}\mathrm{AB}$, we draw arcs on both sides of the line segment AB.
(ii) Again we take B as centre and with same radius we draw arcs on both sides of the line segment AB intersecting the previous arcs at points P and Q respectively.
(iii) We join PQ which is intersecting line segment AB at point R.
(iv) PQ is the required perpendicular bisector of line segment AB; then we have PR is perpendicular on AB
AR = BR, i.e. R is midpoint of AB.
Construction 3
To construct an angle of 60° at the initial point of a given ray
Given a ray AB with initial point A. We have to draw a ray AC such that, $\angle \mathrm{BAC}={60}^{°}$

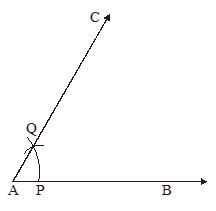
Step of Construction :
(i) For given ray AB, with centre A and with any convenient radius we draw an arc intersecting AB at point P.
(ii) Now with centre P and with the same radius as in step (i) we draw an arc intersecting the previous arc at point Q.
(iii) We join AQ and produce it to form ray AC. Then we have $\angle BAC={60}^{°}$.
12.3. Some Constructions of Triangles
Construction 4
To construct a triangle with given base, a base angle and sum of other two sides.
Example 1
Draw a triangle in which QR = 4.1 cm, and PQ + PR = 7 cm
Solution

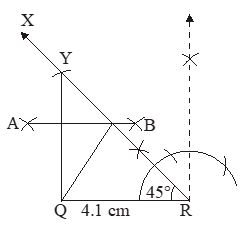
(i) We draw QR = 4.1 cm.
(ii) At R, we draw ray RX such that $\angle \mathrm{R}=45°$.
(iii) From RX, we cut off RY = 7 cm.
(iv) We join QY.
(v) We draw perpendicular bisector AB of QY intersecting RY at P.
(vi) We join PQ. PQR is the required triangle.
Construction 5
To construct a triangle with given base, a base angle and the difference of the other two sides
Example 2
Draw a triangle in which BC = 3.4 cm and AB – AC = 1.3 cm
Solution
Steps of Construction :

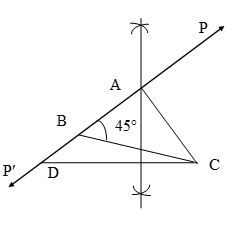
(i) We draw BC = 3.4 cm.
(ii) At point B, we draw $\angle \mathrm{CBP}=45°$.
(iii) We produce BP to forming line PBP’.
(iv) From ray BP’, we cut off BD = 1.3 cm.
(v) We join CD.
(vi) We draw perpendicular bisector of CD meeting BP at point A.
Construction 6
To construct a triangle whose perimeter and two base angles are given
Example 3
Draw a triangle in which $\angle A=60°,\angle B=30°$ and PQ + QR + PR = 10.5 cm.
Solution
Steps of Construction

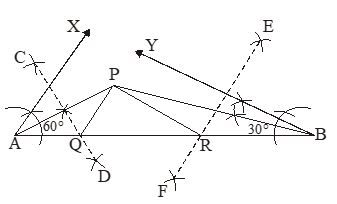
(i) We draw a line segment AB = 10.5 cm.
(ii) We draw $\angle \mathrm{XAB}=60°$ and $\angle \mathrm{ABY}=30°$.
(iii) We draw angle bisectors of $\angle \mathrm{XAB} \mathrm{and} \angle \mathrm{ABY}$ intersecting at point P.
(iv) We draw perpendicular bisectors CD at AP and EF of BP intersecting AB at point Q and R respectively.
(v) We join PQ and PR.
(vi) $△\mathrm{PQR}$ is the required triangle.