9.1. INTRODUCTION
If there are four points in a plane in such a way that no three of them are collinear, then the figure obtained by joining four points, in order is called a quadrilateral. We can say that a quadrilateral is a closed figure with four sides :
e.g. ABCD is a quadrilateral which has four sides AB, BC, CD and DA, four angles and four vertices A, B, C and D and also has two diagonals AC and BD. i.e. A quadrilateral has four sides, four angles, four vertices and two diagonals.
9.2. ANGLES SUM PROPERTY OF A QUADRILATERAL
Theorem : The sum of the angles of a quadrilateral is 360o
Given : Let ABCD be a quadrilateral and AC be its one diagonal

To prove : A + B + C + D = 360o
Solution : In ACD, we have
DAC + ACD + D = 180o … (i)
[Angles sum property]
In ABC, we have
BAC + ACB + B = 180o … (ii)
[Angles sum property]
Adding (i) and (ii), we get
DAC + ACD + D + BAC + ACB + B
= 180o + 180o
(DAC + BAC) + (ACD + ACB) + D + B = 360o
A + C + D + B = 360o
Hence, A + B + C + D = 360o Proved.
9.3. TYPES OF QUADRILATERALS
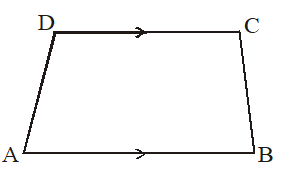
I. A Trapezium : In a quadrilateral if one pair of opposite sides is parallel, then it is called a trapezium i.e. If AB || CD then quadrilateral ABCD is a trapezium.
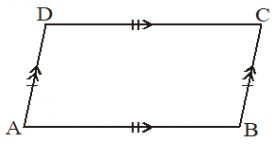
II. A parallelogram : In a quadrilateral, if both pairs of opposite sides are parallel and equal, then it is called a parallelogram. i.e., AB || CD and AB = CD; AD || BC and AD = BC, then ABCD is a parallelogram.
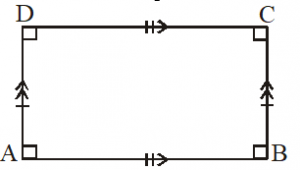
III. A Rectangle : In a quadrilaterals (parallelogram) if all angles are right angles, then it is called a rectangle. i.e. AB || CD, AB = CD, AD || BC; AD = BC and A = B = C = D = 90o, then ABCD is a rectangle.
IV A Rhombus : In a quadrilaterals (parallelogram) if all sides are equal, then it is called a rhombus , i.e., AB || CD, AD || BC and AB = BC = CD = DA, then ABCD is a rhombus.
V A Square : In a quadrilateral (parallelogram) if all sides are equal and all angles are 90o, then it is called a square. i.e. AB || CD, AD || BC, AB = BC = CD = DA and A = B = C = D = 90o
VI A Kite : In a quadrilateral ABCD, if AD = CD and AB = CB, then it is called a kite; i.e., two pairs of adjacent sides are equal but it is not a parallelogram.
LEARN IT
(i) A square is a rectangle and also a rhombus
(ii) A parallelogram is a trapezium
(iii) A trapezium is not a parallelogram
(iv) A trapezium is not a parallelogram
(v) A rectangle or a rhombus is not a square.
9.4. PROPERTIES OF A PARALLELOGRAM
Theorem : A diagonal of a parallelogram divides it into two congruent triangles.
Given : ABCD is a parallelogram and AC be diagonal.
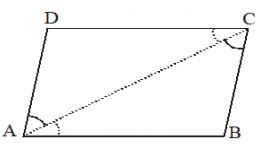
To prove : ABC CDA,
Solution : In ABC and CDA, we have
BC || AD and AC is a transversal
BCA = DAC [Pair of alternate angles]
Similarly, AB || DC and AC is a transversal
BAC = DCA [Pair of alternate angles]
and AC = AC [Common]
Hence, ABC CDA [By ASA congruence rule]
i.e. Diagonal AC divides parallelogram ABCD into two congruent triangles ABC and CDA.
Theorem : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Given : Let ABCD be a quadrilateral in which AB = CD and BC = AD .
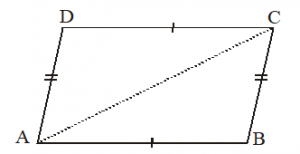
To prove : ABCD is a parallelogram.
Construction : Joined AC
Solution: In ABC and CDA, we have
AB = CD [Given]
BC = AD [Given]
and AC = AC [Common]
[By SSS congruence rule]
CAB = ACD … (i)
and ACB = CAD … (ii) [By CPCT]
Now, line AC intersects AB and DC at A and C, such that
CAB = ACD [From (i)]
But these are alternate interior angles
AB || DC … (iii)
Similarly, line AC intersects BC and AD at C and A such that
ACB = CAD [from (ii)]
But these are alternate interior angles
BC || AD … (iv)
From (iii) and (iv), we have
AB || DC and BC || AD
Hence, ABCD is a parallelogram. Proved.
Theorem : In a parallelogram, opposite angles are equal.
If ABCD is a parallelogram,
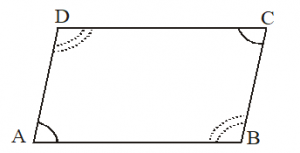
Then, A = C and B = D
Theorem : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Given : ABCD is a quadrilateral in which A = C and B = D .
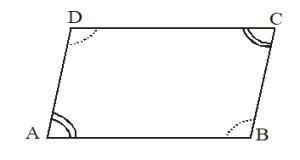
To prove : ABCD is a parallelogram
Solution : In quadrilateral ABCD, we have
A = C … (i) [Given]
B = D …(ii) [Given]
Now, adding (i) and (ii) we get
A + B = C + D … (iii)
We know that the sum of the angles of a quadrilateral is 360o.
A + B + C + D = 360o
A + B) + (A + B) = 360o [From (iii)]
A + B = 180o … (iv)
i.e. A + B = C + D = 180o … (v)
[From (iii) and (iv)]
line AB intersects AD and BC at A and B respectively, such that
A + B = 180o
[The sum of consecutive interior angles is 180o]
AD || BC … (vi)
Again, A + B = 180o
C + B = 180o [ A = C given]
Line BC intersects AB and DC at A and C respectively, such that
B + C = 180o
AB || DC [The sum of consecutive interior angles is 180o] … (vii)
From (vi) and (vii), we get
AD || BC and AB || DC
Hence, ABCD is a parallelogram.
Theorem : The diagonals of a parallelogram bisect each other.
Given : ABCD is a parallelogram in which AB = CD, AB || CD and BC = AD; BC || AD diagonals AC and BD intersect each other at O.
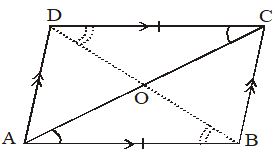
To prove :
OA = OC and OB = OD
Solution :
In OAB and OCD
AB || CD and BD is a transversal [Given]
ABD = CDB [Pair of alternate angles]
BAO = CDO
Again, BC || AD and AC is a transversal [Given]
BAC = DCA [Pair of alternate angles]
BAO = DCO
and AB = CD [Given]
[By ASA congruence rule]
Hence, OA = OC [By CPCT] and OB = OD Proved.
Converse of the above Theorem
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Given :
Let ABCD be a quadrilateral in which diagonals AC and BD bisect each other at O;
i.e. OA = OC and OB = OD.
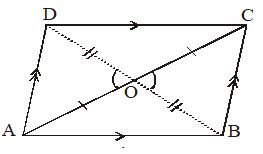
To prove :
ABCD quadrilateral is a parallelogram
Solution:
In AOD and COB, we have
AO = CO [Given]
OD = OB [Given]
and AOD = BOC [Vertically opposite angles]
[By SAS congruence rule]
OAD = OCB [By CPCT] … (i)
But these are alternate interior angles
AD || BC. Similarly, AB || CD
Hence, ABCD is a parallelogram. Proved.
Theorem :
A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel
Given :
ABCD is a quadrilateral in which AB = CD and AB || CD .
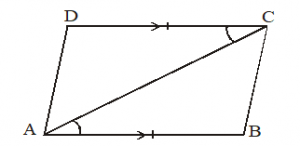
To prove :
ABCD is a parallelogram.
Construction :
Joined AC.
Solution:
In ABC and CDA, we have
AB = CD [Given]
AC = AC [Common]
and BAC = DCA
[ AB||CD and AC is a transversal. Alternate interior angles are equal]
[SAS congruence rule]
BCA = DAC [By CPCT]
But these are alternate angles.
AD || BC
Now, AB || CD and AD || BC. Hence, quadrilateral ABCD is a parallelogram. Proved.
9.5. MIDPOINT THEOREM
The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Given :
ABC is a triangle in which D and E are the mid-points of sides AB and AC respectively DE is joined.
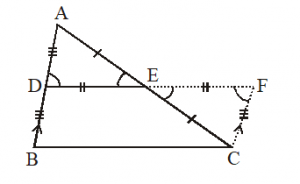
To prove :
DE || BC and DE = 1/2 BC
Construction : Line segment DE, is produced to F, such that DE = EF joined FC.
Proof : In AED and CEF, we have
AE = CE [ E is the midpoint of AC Given]
AED = CEF [vertically opposite angles]
and DE = EF [By construction]
[By SAS congruence rule]
AD = CF … (i) [By CPCT]
and ADE = CFE … (ii) [By CPCT]
Now, D is the mid-point of AB
AD = BD
DB = CF … (iii) [From (i) AD = CF]
DF intersects AD and FC at D and F respectively such that
ADE = CFE … [From (ii)]
i.e. alternate interior angles are equal
AD || FC
DB || CF … (iv)
From (iii) and (iv), we get that DBCF is a quadrilateral such that one pair side is equal and parallel
DBCF is a parallelogram
DF || BC and DF = BC [ opposite sides of a || gm are equal are parallel]
But, D, E, F are collinear and DE = EF
Hence, DE || BC and DE = ½ BC. Proved.
Converse of above Theorem : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
Given : Let ABC be a triangle in which E is the mid-point of AB, line l is passing through E and is parallel to BC, and CM || BA intersects AC at point F.
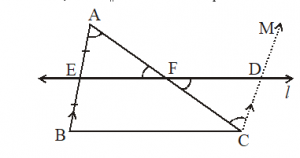
To prove : AF = CF
Construction : CM || BE and intersecting line l at D is drawn
Proof : CM || BE and l || BC
BCDE is a parallelogram.
BE = CD [opposite sides of a ||gm]
But BE = AE [Given]
AE = CD … (i)
Now, in AEF and CDF, we have
AFE = CFD [vertically opposite angles]
A = FCD [Alternate angles]
AE = CD … [from (i)]
[AAS congruence rule]
Hence, AF = CF [CPCT].








