10.1. INTRODUCTION
The part of the plane enclosed by a simple closed figure is called a planar region corresponding to that figure. The measurement of this planar region is called area. Hence, the area of a figure is a number with square unit.
Two figures are called congruent; if they have the same shape and the same size. Because of this reason, if two figures are congruent they must have equal area. But, if two figures have equal areas, they need not be congruent.
Example.
(i)
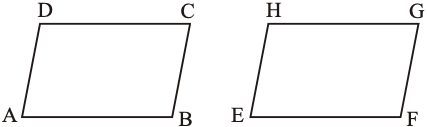
||gm ABCD ||gm EFGH
Area of ||gm ABCD = Area of ||gm EFGH.
(ii) 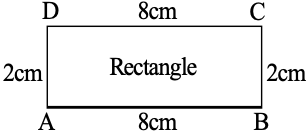
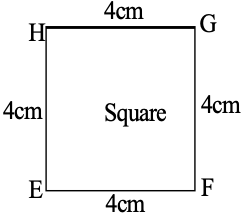
Area of a rectangle ABCD = Area of square = EFGH
But, the rectangle ABCD is not congruent to the square EFGH
10.2.FIGURES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS
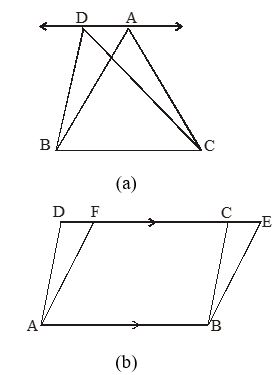
In Fig. a, DA || BC, ABC and DBC have the same base BC and are in between the same parallels DA and BC.
In Fig. b, parallelogram ABCD and parallelogram ABEF have the same base AB and are in between the same parallels AB and DE.
10.3. PARALLELOGRAMS ON THE SAME BASE AND BETWEEN THE SAME PARALLELS
Theorem
Parallelograms on the same base and in between the same parallels are equal in area.
Given:
ABCD and ABEF are two parallelograms, on the same base AB and in between the same parallels AB and DE in figure
To prove:
ar(ABCD) = ar(ABEF)
Proof:
In ADF and BCE, we have
ADF = BCE
[corresponding angles from AD || BC and transversal DE]
AFD = BEC
[corresponding angles from AF || BE and transversal DE]
DAF = CBE
[Angles sum property of a triangle]
Also, AD = BC
[opposite sides of the ||gm ABCD]
[By ASA congruence rule]
ar(ADF) = ar(BCE)
[congruent figures have equal areas]
Now, ar(ABCD) = ar(ADF) + ar(ABCF) = ar(BCE) + ar(ABCF)
ar(ABCD) = ar(ABEF)
Hence, parallelograms ABCD and ABEF are equal in area. Proved.
Example 1
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in X and CD in Y. Prove that:
ar(AXYD) = ar(||gm ABCD)
Given:
ABCD is a parallelogram in which its diagonals AC and BD intersect each other at O. A line through O meet AB in X and CD in Y in figure.

To prove:
ar(AXYD) = ar(||gm ABCD)
Solution:
A diagonal of a ||gm divides it into two triangles of equal areas.
Diagonal AC of ||gm ABCD divides it into two triangles of equal areas
ar(DACD) = ar(||gm ABCD) … (i)
Now, in sAOX and COY, we have:
AOX = COY
[vertically opposite angles]
AO = CO
[diagonals of a ||gm bisect each other i.e. O is the mid-point of AC.]
and OAX = OCY
[ AB || DC and AC is a transversal
CAB = ACDOAX = OCY ]
AOX COY
[By ASA congruence rule]
ar(AOX) = ar(COY)
[By congruent area axiom]
ar(AOX)+ar(AOYD) =ar(COY)+ ar(AOYD)
[Adding both sides ar(AOYD)]
ar(AXYD) = ar(ACD) …(ii)
From (i) and (ii), we get
ar(AXYD) = ar(||gm ABCD)
Example 2
A quadrilateral ABCD is such that diagonal BD divides area in two equal parts. Prove that BD bisects AC.
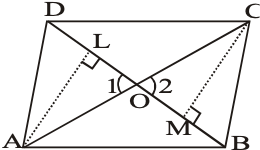
Given:
ABCD is a quadrilateral in which diagonal BD bisects it i.e. ar(ABD) = ar(BCD)
To prove:
OA = OC
Construction:
Join AC, which intersects at O. Also ALBD and CMBD have been drawn.
Solution:
ar(ABD) = ar(BCD) [Given]
Now, ABD and ABC are on the same base AB and have equal areas.
Their corresponding altitudes are equal i.e. AL = CM …..(i)
Again, in ALO and CMO, we have
1 = 2 [Vertically opposite angles]
ALO = CMO [Each equal to 90o]
and AL = CM [From (i)]
[By AAS congruence rule]
AO = OC [By CPCT]
Hence, BD bisects AC.
Example 3
E, F, G, H are respectively the mid-points of the sides AB, BC, CD and DA of parallelogram ABCD. Prove that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram ABCD, i.e. ar(EFGH) = ar(ABCD)
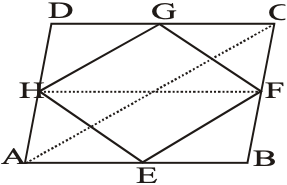
Given:
ABCD is a quadrilateral in which E, F, G, H are respectively the mid-points of the sides AB, BC, CD and DA in figure.
To prove:
(i) Quadrilateral EFGH is a parallelogram
(ii) ar(||gm EFGH) = ar(||gm ABCD)
Construction:
Joined AC and HF.
Solution:
In ABC, E and F are the mid-points of sides AB and BC respectively.
EF || AC and EF = AC …(i)
[By mid-point Theorem]
Similarly, in ADC, G and H are mid-points of sides DC and AD respectively
GH || AC and GH = AC …(ii)
[By mid-point theorem]
From (i) and (ii), we get
EF || GH and EF = GH
EFGH is a parallelogram
[ one pair of opposite sides are parallel and equal]
Now, ABCD is a parallelogram
AD = BC and AD || BC
AD = BC and AD || FC [FC = BC]
HD = FC and AD || FC or HD || FC
HDFC is a parallelogram
[ one pair of opposite sides are parallel and equal]
Again, HFG and ||gm HDCF are at the same base HF and in between the same parallel lines HF and DC.
ar(HGF) = ar(||gm HDCF) …(iii)
Similarly, HEF and ||gm HABF are on the same base HF and in between the same parallels HF and AB.
ar(HEF) = ar(||gm HABF) …(iv)
Adding (iii) and (iv), we get
ar(HGF) + ar(HEF) = ar(||gm HDCF) + ar(||gm HABF)
[ar || gm HDCF + ar || gm HABF]
Hence, ar(||gm EFGH) = ar(||gm ABCD)
10.4. TRIANGLES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS
Theorem
Two triangles on the same base (or equal bases) and in between the same parallels are equal in area.
Given:
ABC and DBC are two triangles on the same base BC and in between the same parallel lines BC and AD in figure.
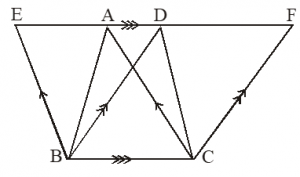
To prove:
ar(ABC) = ar(DBC)
Construction:
Through B, BE || CA has been drawn meeting is DA produced in E and through C, CF || BD has been drawn and is meeting AD produced in F.
Proof:
BE || CA and EA || BC [By construction]
BCAE is a parallelogram
Again, CF || BD and DF || BC [By construction]
BCFD is a parallelogram
Now, parallelogram BCAF and BCFD are on the same base BC and in between the same parallel lines BC and EF.
ar(||gm BCAE) = ar(|| gm BCFD) …(i)
But, we know that the diagonal of a ||gm divides it into two triangles of equal area
ar(ABC) = ar(||gm BCAE) …(ii)
and ar(DBC) = ar(||gm BCFD) …(iii)
From (i), (ii) and (iii), we get
ar(ABC) = ar(DBC) Proved.
LEARN IT
Two triangles having the same base (or equal bases) and equal area lie between the same parallels.
Theorem
Prove that area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height).
Given:
ABC is a triangle in which BC is the base and AM is the corresponding height in figure.
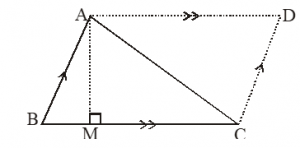
Construction:
Through A and C, AD || BC and CD || BA are drawn and they intersect each other at D.
Proof:
AD || BC and CD || BA [By construction]
ABCD is a parallelogram
Now, diagonal AC divides the ||gm ABCD into two triangles of equal areas.
ar(ABC) = × ar(||gm ABCD)
= × BC × AM
[ ar(||gm ABCD) = base × height]
Hence, ar(ABC) = × base × height.
Example 4
A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the area of a pair of opposite triangles so formed is equal to the sum of the areas of other pair of triangles.
Given:
ABCD is a rectangle in which O is a point inside it in figure. OA, OB, OC and OD have been joined.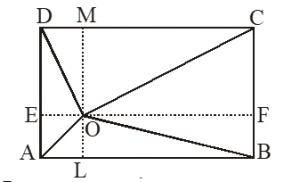
To prove:
ar(AOD) + ar(BOC) = ar(AOB) + ar(COD)
Construction:
EOF || AB or DC and MOL || AD or BC have been drawn
Solution:
ar(AOD) + ar(BOC) = (AD × OE) + (BC × OF)
= (AD × OE) + (AD × OF) [ AD = BC]
= AD (OE + OF)
= (AD) × (EF)
ar(AOD) + ar(BOC)
= ar(rect. ABCD) …(i)
Again, ar(AOB) + ar(COD) = (AB × OL) + (CD × OM)
= (AB × OL) +(AB × OM) [ AB = CD]
= AB (OL + OM) = AB × LM
= AB × AD [ LM = AD]
ar(AOB) + ar(COD)
= ar(rect. ABCD) …(ii)
Hence, ar(AOD) + ar(BOC) = ar(AOB) + ar(COD)
Example 5
In a parallelogram ABCD, E, F are any two points on the sides AB and BC respectively.
Prove that ar(ADF) = ar(DCE)
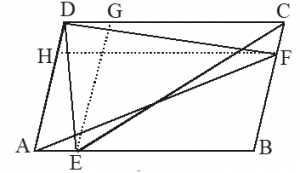
Given:
ABCD is a parallelogram in which E and F are any two points on the sides AB and BC respectively in figure.
Construction:
Joined DE, EC and DF, AF. Also FH || AB and EG || AD have been drawn.
To prove:
ar(ADF) = ar(DCE)
Solution:
FH || AB [By construction]
and AH || BF [Given ABCD is a ||gm]
ABFH is a parallelogram [Two pair of opposite sides are parallel]
Now, AF is a diagonal of ||gm ABFH
ar(AFH) = ar(||gm ABFH) …(i)
In ||gm DCFH, DF is a diagonal
ar(DFH) = ar(||gm DCFH) …(ii)
Adding (i) and (ii), we get
ar(AFH) + ar(DFH) = ar(||gm ABFH) + ar(||gm DCFH)
ar(ADF) = ar(||gm ABCD) … (iii)
In ||gm AEGD, DE is a diagonal
ar(DEG) = (||gm AEGD) … (iv)
||gm CBEG, CE is a diagonal,
ar(CEG) = ar(||gm CBEG) … (v)
Adding (iv) and (v), we get
ar(DEG) + ar(CEG) = ar(||gm AEGD) + ar(||gm CBEG)
ar(DEG) + ar(CEG) = ar[||gm AEGD + ||gm CBEG]
ar(DCE) = ar(||gm ABCD) …(vi)
From (iii) and (vi), we get
ar(ADF) = ar(DCE)








