Polynomials

2.1 Introduction
In mathematics, a polynomial is a finite length expression constructed from variables (also known as indeterminates) and constants, using the operations of addition, subtraction, multiplication, and constant non-negative whole number exponents. For example, ${\mathrm{x}}^2$ – 4x + 7 is a polynomial, but ${\mathrm{x}}^2–\frac{4}{\mathrm{x}}+7{\mathrm{x}}^{3/2}$ is not, because its second term involves division by the variable x and also because its third term contains an exponent that is not a whole number.
Polynomials are one of the most important concepts in algebra and throughout mathematics and science. They are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics, and are used in calculus and numerical analysis to approximate other functions. Polynomials are used to construct polynomial rings, one of the most powerful concepts in algebra and algebraic geometry. Before we go into the detail study, let us recap few basic terms that we learnt in our earlier classes.
2.2 Basic terms
i) Variable: A symbol which takes various values is known as a variable or literal. Any letter can be used to denote a variable.
Example: x, y, z, etc.
ii) Constant: A symbol having a fixed numerical value is called a constant.
Example: 3, 25,8, etc.
iii) Coefficient: In the product of a variable and a constant, each is called the coefficient of the other.
Example: 3x. Here 3 is the coefficient of x and also x is called the coefficient of 3.
iv) Term: Numbers and literals are multiplied to form a product which is known as the term. Also, a constant or a variable is also known as a term.
Example: 3x, 4, y, 5y, etc.
v) Algebraic Expression
A combination of constants and variables by the four basic mathematical operations (+, –, ×, $÷$) is called an Expression or an Algebraic Expression.
Example:
3${\mathrm{x}}^2$ + 4x – 3 , $4{\mathrm{x}}^{\frac{1}{3}}+3\sqrt{\mathrm{x}}+5$ , 4${\mathrm{x}}^2$+ 3x + 5
Note: The powers of variables of an algebraic expression can take any real number.
Example: In the expression $3{\mathrm{x}}^2+4\mathrm{x}–3$ , x is the variable, 3, 4 are coefficients, –3 is the constant and the total number of terms in the expression are 3.
2.3 Polynomial
An expression of the form
p(x) = ${\mathrm{a}}_0+{\mathrm{a}}_1\mathrm{x}+{\mathrm{a}}_2{\mathrm{x}}^2+\dots \dots .+{\mathrm{a}}_{\mathrm{n}}{\mathrm{x}}^{\mathrm{n}}$
where powers o f variable are non–negative integers, and coefficients are any real numbers $\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{a}}_1,{\mathrm{a}}_2\dots {\mathrm{a}}_{\mathrm{n}}\in \mathrm{R}\right)$. is called a polynomial in x of ${\mathrm{n}}^{\mathrm{th}}$ degree over real numbers.
Example: $\left({\mathrm{x}}^4–3{\mathrm{x}}^2+7\right),\left(4{\mathrm{x}}^3+3\mathrm{x}\right),\dots$ etc.
General form of a polynomial
Polynomials with their standard or general forms and their respective degrees are given in the table below :

2.4 Degree of polynomial
I. Degree of a polynomial in one variable
In case of a polynomial in one variable, the highest power of the variable is called the degree of the polynomial.
Examples:
i) $4{\mathrm{x}}^3–7\mathrm{x}+\frac{7}{8}$  is a polynomial in x of degree 3.
ii) $3{\mathrm{x}}^5–7$ is a polynomial in x of degree 5.
II. Degree of a polynomial in two or more variables
In the case of polynomials in more than one variable, the sum of the powers of the variables in each term is taken up and the highest sum so obtained is called the degree of the polynomial.
Examples:
i) $3{\mathrm{x}}^2–5x^3{y}^2+9\mathrm{y}$ is a polynomial of degree 5 in x and y.
ii) $7{\mathrm{x}}^2{\mathrm{yz}}^3=+4{\mathrm{xy}}^2{\mathrm{z}}^4–2{\mathrm{x}}^2\mathrm{y}$ is a polynomial of degree 7 in x, y and z.
2.5 Zero of Polynomial
A real number a is a zero of a polynomial P(x) if P(a) = 0.
Example: Let P(x) = ${\mathrm{x}}^2$ – 5x + 6
Put x = 2$\Rightarrow$P(2) = $2^2$ – 5 (2) + 6 = 4 – 10 + 6 = 0
Put x = 3$\Rightarrow$P(3) = $3^2$ – 5 (3) + 6 = 9 – 15 + 6 = 0.
2, 3 are the zeroes of the polynomial, $\mathrm{P}\left(\mathrm{x}\right)={\mathrm{x}}^2–5\mathrm{x}+6$
Note:
i) The number of zeros of a polynomial is equal to the degree of the polynomial.
ii) Every linear polynomial in one variable has a unique zero.1
2.6 Classification of polynomials
Based on different criteria, we have different types of classifications.
I. Classification based on number of terms

II. Classification based on coefficients

III. Classification based on degree

2.7 Arithmetic operations polynomials
Before we see the arithmetic operations related to polynomials, let us know about like terms and unlike terms in a polynomial.
Like terms : Terms with the same variables and which have the same exponents are called like or similar terms.
Example: $3{\mathrm{x}}^3,–7{\mathrm{x}}^3,\frac{1}{5}{\mathrm{x}}^3\dots \dots$ etc. are like terms.
Unlike terms: Terms with different variables and which have different exponents are called unlike terms.
Example: ${\mathrm{x}}^2\mathrm{y},–5{\mathrm{x}}^3,\frac{4}{3}{\mathrm{xy}}^2\dots$ etc. are unlike terms.
Now, let us know about the arithmetic operations of polynomials.
I. Addition of Polynomials
Two or more polynomials can be added by arranging their terms and combining the like terms.
Let us see the addition of $3{\mathrm{x}}^2–5\mathrm{xy}+2{\mathrm{y}}^2$ and $–7{\mathrm{x}}^2+2\mathrm{xy}+4{\mathrm{y}}^2$.
$\begin{array}{c}3{\mathrm{x}}^2–5\mathrm{xy}+2{\mathrm{y}}^2\\ \underline{–7{\mathrm{x}}^2+2\mathrm{xy}+4{\mathrm{y}}^2}\\ –4{\mathrm{x}}^2–3\mathrm{xy}+6{\mathrm{y}}^2\end{array}$
($\because$ like terms are placed one below the other)
Properties of Addition of Polynomials

II. Subtraction of Polynomials
For subtraction of polynomials, we need to rearrange the terms of the two polynomials so that the like terms can occur in vertical columns. Now, change the sign of each term of the polynomial to be subtracted and then add the two polynomials.
Let us subtract $3{\mathrm{y}}^2–11\mathrm{xy}–2{\mathrm{x}}^2$ from $5{\mathrm{x}}^2+7\mathrm{xy}–2{\mathrm{y}}^2$
$\begin{array}{c}5{\mathrm{x}}^2+7\mathrm{xy}–2{\mathrm{y}}^2\\ \underline{\underset{+}{–}2{\mathrm{x}}^2\underset{+}{–}11\mathrm{xy}\underset{–}{+}3{\mathrm{y}}^2}\\ 7{\mathrm{x}}^2+18\mathrm{xy}–5{\mathrm{y}}^2\end{array}$
III. Multiplication of Polynomials
The following are some points to be noted for multiplying polynomials.
i) The general rule is that each term in the first factor has to multiply each term in the other factor.
ii) The number of products you get has to be the number of terms in the first factor times the number of terms in the second factor.
For example, a binomial times a binomial gives four products, while a binomial times a trinomial gives six products.
iii) Be very careful and methodical to avoid missing any terms.
iv) After the multiplication is complete, you can try to collect like terms and write side by side and simplify the result.
Multiplication of polynomials can be done in two ways: Here p(x) is called the multiplication and q(x) the multiplier.
1. Horizontal Method:
Step – 1: Multiply each term p(x) with that of q(x).
p(x) = x + 3
q(x) = x – 2
$\mathrm{p}\left(\mathrm{x}\right) \times \mathrm{q}\left(\mathrm{x}\right) = (\mathrm{x} + 3) \times (\mathrm{x} – 2)$
= x(x – 2) + 3(x – 2)
Step $–$2: Now, group the like terms, retaining their signs and add the coefficients of like powers.
x (x – 2) + 3 (x – 2)
= ${\mathrm{x}}^2$ – 2x + 3x – 6
= ${\mathrm{x}}^2$ + x – 6 (product)
2.Column method:
Step – 1: Every term of first expression should be multiplied with first term of second expression.
Step – 2: Every term of first expression should be multiplied with second term of second expression.
Step – 3: Continue until all the terms of second expression are multiplied.
Let us find the product of $3{\mathrm{x}}^2–2\mathrm{x}+1$ and $2{\mathrm{x}}^2–3\mathrm{x}+4$ using the above method.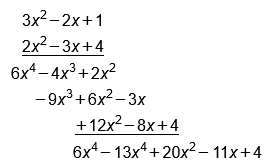

In this method, we write multiplicand and the multiplier in descending powers of x, arrange one under another, and multiply the multiplicand by every term of the multiplier and add.
Properties of Multiplication of Polynomials

Note : For the polynomial x ($\ne$0), the multiplicative inverse is $\frac{1}{\mathrm{x}}$ , but it is not a polynomial. Therefore polynomials do not possess multiplicative inverses.
IV. Division of Polynomials
The following two methods are used for division of polynomials.
1. Long Division Method
Step – 1: Arrange the terms of the dividend and divisor in descending order of their degrees.
Step – 2: Divide the first term of the dividend by the first term of the divisor to obtain the first term of the quotient.
Step – 3 : Multiply all the terms of the divisor by the first term of the quotient and subtract the result from the dividend.
Step – 4 : Consider the remainder as a new dividend and proceed as before.
Step – 5 : Repeat this process till we obtain a remainder which is either 0 or a polynomial of degree less than that of the divisor.
Example: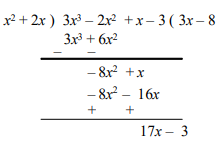

Note : If any terms are missing in the dividend or divisor, leave spaces and treat them as terms with coefficient zero.
2. Synthetic division method
As this is short and simple it is called synthetic division.
This is also called Horner’s method.
Let us understand the method by considering the following example.
Divide ${\mathrm{x}}^3+6{\mathrm{x}}^2+11\mathrm{x}+10 \mathrm{by} \mathrm{x}+1$

Step 1: Arrange the coefficients of the dividend in descending order of powers of variables (Row–1).
1            6              11              10
Step 2: The required divisor is obtained by taking the zero of the original divisor.
i.e., x + 1 = 0 $\Ri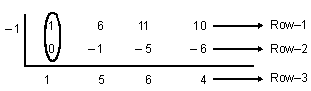ghtarrow$ x = – 1

Step 3: The first element of Row–2 is always a zero (0).
Step 4: The first element of Row–3 is obtained by adding first elements of Row–1 and Row–2.
1 + 0 =1
Note: i) ${\mathrm{n}}^{\mathrm{th}}$ element of Row–3 = ${\mathrm{n}}^{\mathrm{th}}$ element of
Row–1 + ${\mathrm{n}}^{\mathrm{th}}$ element of Row–2.
ii) ${\mathrm{n}}^{\mathrm{th}}$ element of Row–2 = divisor × ${\left(\mathrm{n}–1\right)}^{\mathrm{th}}$ element of Row–3  [n > 1].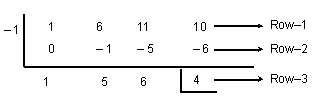

Step 5: The last element of Row–3 is the required remainder. Remainder = 4
Step 6: The number in Row–3 (except the last) represents the coefficients of the quotient, which is one degree less than the dividend.

$\therefore$ Quotient = ${\mathrm{x}}^2$ + 5x + 6 and Remainder = 4
Note :
1) ${\mathrm{x}}^{\mathrm{n}} – {\mathrm{y}}^{\mathrm{n}}$  is divisible by (x – y) for both even and odd values of n.
2) ${\mathrm{x}}^{\mathrm{n}}+{\mathrm{y}}^{\mathrm{n}}$ is divisible by (x + y) only for odd values on n.
3) This method is applicable only for dividing a polynomial by a linear polynomial.
2.8 Remainder theorem
Division Algorithm
Dividend = Divisor $\times$Quotient + Remainder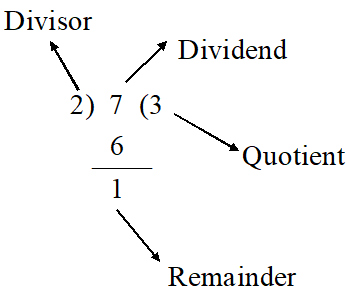

So, 7 = (2 × 3) + (1) = 7
Hence, the division algorithm.
Remainder Theorem
If polynomial f (x) is divided by a linear polynomial (x – a), then the remainder is f(a).
For example, let us find the remainder when $27{\mathrm{x}}^3–9{\mathrm{x}}^2+11\mathrm{x}–4$ is divided by x–2.
Given that $\mathrm{f}\left(\mathrm{x}\right)=27{\mathrm{x}}^3–9{\mathrm{x}}^2+11\mathrm{x}–4$ is divided by x–2. Then by remainder theorem, the remainder is f(2)
$$\begin{gathered} \Rightarrow f\left(2\right)=27(2{)}^3–9(2{)}^2+11\left(2\right)–4 \\ =27\times 8–9\times 4+22–4 \\ =216–36+22–4=198 \end{gathered}$$
Therefore, the remainder is 198.
Note: If a polynomial f(x) is divided by (x – a), then the remainder is f(a)given by equating the x – a to zero. That is, x – a = 0 or x = a. That means, we have to substitute a for x in f (x).
Remainder on division of f(x) by (x – a), (x + a), (ax – b) and (ax + b) are shown as in the table below:

Note: This method is not applicable if the divisor is a non-linear polynomial.
2.9 FACTORIZATION OF POLYNOMIALS
Factor Theorem
If a polynomial f (x) is divided by a linear polynomial (x – a) and the remainder is zero (f(a) = 0), then (x – a) is said to be a factor of f (x).
Let us check if ${\mathrm{x}}^2–5\mathrm{x}+6$ is a factor of $2{\mathrm{x}}^4–17{\mathrm{x}}^3+49{\mathrm{x}}^2–52\mathrm{x}+12$ or not.${\mathrm{x}}^2–5\mathrm{x}+6=(\mathrm{x}–2)(\mathrm{x}–3)$
If (x – 2) is a factor, then f(2) should be zero.
$\mathrm{f}\left(2\right)=2(2{)}^4–17(2{)}^3+49(2{)}^2–52(2)+12$
= 32 – 136 + 196 – 104 + 12 = 0
$\therefore$ (x–2) is a factor.
Similarly, if (x–3) is a factor, then f(3) should be zero.
$\mathrm{f}\left(3\right)=2(3{)}^4–17(3{)}^3+49(3{)}^2–52(3)+12$
= 162 – 459 + 441 – 156 + 12 = 0
Therefore, (x – 3) is a factor.
Hence, (x – 2)(x – 3) = $x^2–5x+6$ is a factor of the given expression.
Some interesting observations:
i) The degree of the remainder is always less than the degree of the divisor.
ii) If the degree of the divisor is greater than the degree of the dividend, then the quotient is zero.
iii) For an expression f(x), If f(0) = 0, then x is a factor of f(x).
iv) For an expression f(x), If f(a) = f(b) = 0, then x – a and x – b are factors of f(x).
2.10 Algebraic Identities
Expressing a given polynomial as a product of two or more factors is called factorisation.
Polynomials can be factorized using the following methods.
I. Method of using Identities
II. Method of Splitting the middle term
III. Method of Completion of squares
IV. Method of Grouping of terms
I. Method of using identities:
In this method, we factorise the polynomials using different identities. Before we see the method of factorisation, let’s recap the identities that we learnt in our earlier classes.
1. $(\mathrm{a}+\mathrm{b}{)}^2={\mathrm{a}}^2+2\mathrm{ab}+{\mathrm{b}}^2$
2. $(\mathrm{a}–\mathrm{b}{)}^2={\mathrm{a}}^2–2\mathrm{ab}+{\mathrm{b}}^2$
3. $(\mathrm{a}+\mathrm{b})(\mathrm{a}–\mathrm{b})={\mathrm{a}}^2–{\mathrm{b}}^2$
4. $(\mathrm{a}+\mathrm{b}{)}^2+(\mathrm{a}–\mathrm{b}{)}^2=2\left({\mathrm{a}}^2+{\mathrm{b}}^2\right)$
5. $(\mathrm{a}+\mathrm{b}{)}^2–(\mathrm{a}–\mathrm{b}{)}^2=4\mathrm{ab}$
6. $(\mathrm{a}+\mathrm{b}+\mathrm{c}{)}^2={\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2+2\mathrm{ab}+2\mathrm{bc}+2\mathrm{ca}$
$={\mathrm{\Sigma a}}^2+2\mathrm{\Sigma ab}$
7. $(\mathrm{a}+\mathrm{b}{)}^3={\mathrm{a}}^3+{\mathrm{b}}^3+3\mathrm{ab}(\mathrm{a}+\mathrm{b})$
$={\mathrm{a}}^2+3{\mathrm{a}}^2\mathrm{b}+3{\mathrm{ab}}^2+{\mathrm{b}}^3$
8. $(\mathrm{a}–\mathrm{b}{)}^3={\mathrm{a}}^3–{\mathrm{b}}^3–3\mathrm{ab}(\mathrm{a}–\mathrm{b})$
$={\mathrm{a}}^3–3{\mathrm{a}}^2\mathrm{b}+3{\mathrm{ab}}^2–{\mathrm{b}}^3$
9. $(\mathrm{x}+\mathrm{a})(\mathrm{x}+\mathrm{b})={\mathrm{x}}^2+(\mathrm{a}+\mathrm{b})\mathrm{x}+\mathrm{ab}$
10. $(\mathrm{x}+\mathrm{a})(\mathrm{x}+\mathrm{b})(\mathrm{x}+\mathrm{c})$
$={\mathrm{x}}^3+{\mathrm{x}}^2(\mathrm{a}+\mathrm{b}+\mathrm{c})+\mathrm{x}(\mathrm{ab}+\mathrm{bc}+\mathrm{ac})+\mathrm{abc}$
11. ${\mathrm{a}}^3+{\mathrm{b}}^3=(\mathrm{a}+\mathrm{b})\left({\mathrm{a}}^2–\mathrm{ab}+{\mathrm{b}}^2\right)$
12. ${\mathrm{a}}^3–{\mathrm{b}}^3=(\mathrm{a}–\mathrm{b})\left({\mathrm{a}}^2+\mathrm{ab}+{\mathrm{b}}^2\right)$
13. ${\mathrm{a}}^3+{\mathrm{b}}^3+{\mathrm{c}}^3–3\mathrm{abc}$
$=(\mathrm{a}+\mathrm{b}+\mathrm{c})\left({\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2–\mathrm{ab}–\mathrm{bc}–\mathrm{ca}\right)$
14. $\text{ If }\mathrm{a}+\mathrm{b}+\mathrm{c}=0\text{ then }{\mathrm{a}}^3+{\mathrm{b}}^3+{\mathrm{c}}^3=3\mathrm{abc}$
15. ${\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2–\mathrm{ab}–\mathrm{bc}–\mathrm{ca}$
$=\frac{1}{2}\left[(\mathrm{a}–\mathrm{b}{)}^2+(\mathrm{b}–\mathrm{c}{)}^2+(\mathrm{c}–\mathrm{a}{)}^2\right]$
i) Factorisation using ${\mathbf{a}}^{\mathbf{2}}\mathbf{2}\mathbf{ab}\mathbf{+}{\mathbf{b}}^{\mathbf{2}}\mathbf{\text{ and }}{\mathbf{a}}^{\mathbf{2}}\mathbf{–}\mathbf{2}\mathbf{ab}\mathbf{+}{\mathbf{b}}^{\mathbf{2}}$
Example: Factorise $49{\mathrm{a}}^2+42\mathrm{ab}+9{\mathrm{b}}^2$.
$49a^2+42ab+9b^2$ can be written as
$(7\mathrm{a}{)}^2+2(7\mathrm{a}\left)\right(3\mathrm{b})+(3\mathrm{b}{)}^2$
Which is of the type ${\mathrm{a}}^2+2\mathrm{ab}+{\mathrm{b}}^2$.
We have ${\mathrm{a}}^2+2\mathrm{ab}+{\mathrm{b}}^2=(\mathrm{a}+\mathrm{b}{)}^2$.
$\therefore 49{\mathrm{a}}^2+42\mathrm{ab}+9{\mathrm{b}}^2=(7\mathrm{a}+3\mathrm{b}{)}^2=(7\mathrm{a}+3\mathrm{b}\left)\right(7\mathrm{a}+3\mathrm{b})$
Example: Factorise  $4(\mathrm{m}+\mathrm{n}{)}^2–28(\mathrm{m}+\mathrm{n})\mathrm{p}+49{\mathrm{p}}^2$.
$4(\mathrm{m}+\mathrm{n}{)}^2–28(\mathrm{m}+\mathrm{n})\mathrm{p}+49{\mathrm{p}}^2$ can be written as
$\left[2\right(\mathrm{m}+\mathrm{n}){]}^2–2[2(\mathrm{m}+\mathrm{n})\left]\right[7\mathrm{p}]+(7\mathrm{p}{)}^2$
which is of the form ${\mathrm{a}}^2–2\mathrm{ab}+{\mathrm{b}}^2$ .
$[2\mathrm{m}+2\mathrm{n}–7\mathrm{p}{]}^2=(2\mathrm{m}+2\mathrm{n}–7\mathrm{p}\left)\right(2\mathrm{m}+2\mathrm{n}–7\mathrm{p})$.
ii) Factorisation using ${\mathbf{a}}^{\mathbf{2}}\mathbf{–}{\mathbf{b}}^{\mathbf{2}}$
Example: Factorise $16{\mathrm{a}}^4–{\mathrm{b}}^4$.
This is of the form $16{\mathrm{a}}^4–{\mathrm{b}}^4={\left(4{\mathrm{a}}^2\right)}^2–{\left({\mathrm{b}}^2\right)}^2$
$\therefore 16{\mathrm{a}}^4–{\mathrm{b}}^4={\left(4{\mathrm{a}}^2\right)}^2–{\left({\mathrm{b}}^2\right)}^2=\left(4{\mathrm{a}}^2+{\mathrm{b}}^2\right)\left(4{\mathrm{a}}^2–{\mathrm{b}}^2\right)$
$=\left(4{\mathrm{a}}^2+{\mathrm{b}}^2\right)\left[(2\mathrm{a}{)}^2–(\mathrm{b}{)}^2\right]$
$=\left[4{\mathrm{a}}^2+{\mathrm{b}}^2\right][2\mathrm{a}+\mathrm{b}][2\mathrm{a}–\mathrm{b}]$
iii) Factorisation using ${\mathbf{a}}^{\mathbf{3}}\mathbf{+}{\mathbf{b}}^{\mathbf{3}}\mathbf{\text{ or }}{\mathbf{a}}^{\mathbf{3}}\mathbf{–}{\mathbf{b}}^{\mathbf{3}}$
Example: Factorise  ${\mathrm{x}}^6+27.{\mathrm{x}}^6+27$ can be rewritten as ${\left({\mathrm{x}}^2\right)}^3+{\left(3\right)}^3$ which is of the form ${\mathrm{a}}^3+{\mathrm{b}}^3$.
$\therefore {\left({\mathrm{x}}^2\right)}^3+{\left(3\right)}^3=\left({\mathrm{x}}^2+3\right)\left({\left({\mathrm{x}}^2\right)}^2–\left({\mathrm{x}}^2\right)\left(3\right)+3^2\right)$
$=\left({\mathrm{x}}^2+3\right)\left({\mathrm{x}}^4–3{\mathrm{x}}^2+9\right)$
Example: Factorise ${\mathrm{x}}^6–729$.
${\mathrm{x}}^6–729$ can be rewritten as ${\left(x^2\right)}^3–{\left(9\right)}^3$
which is of the form ${\mathrm{a}}^3–{\mathrm{b}}^3$.
$\therefore {\left({\mathrm{x}}^2\right)}^3{\left(9\right)}^3=\left({\mathrm{x}}^2–9\right)\left({\left({\mathrm{x}}^2\right)}^2+\left({\mathrm{x}}^2\right)\left(9\right)+9^2\right)$
$=\left({\mathrm{x}}^2–9\right)\left({\mathrm{x}}^4+9{\mathrm{x}}^2+81\right)$
$=(\mathrm{x}+3)(\mathrm{x}–3)\left({\mathrm{x}}^4+9{\mathrm{x}}^2+81\right)$
iv) Factorisation using ${\mathbf{a}}^{\mathbf{3}}\mathbf{+}{\mathbf{b}}^{\mathbf{3}}\mathbf{+}{\mathbf{c}}^{\mathbf{3}}\mathbf{–}\mathbf{3}\mathbf{abc}$.
Example: Factorise $x^3–8y^3–24xy–64$.
Clearly, $(\mathrm{x}{)}^3+(–2\mathrm{y}{)}^3+(–4{)}^3–3(\mathrm{x}\left)\right(–2\mathrm{y}\left)\right(–4)$ is of the form ${\mathrm{a}}^3+{\mathrm{b}}^3+{\mathrm{c}}^3–3\mathrm{abc}$
$\therefore {\mathrm{x}}^3–8{\mathrm{y}}^3–24\mathrm{xy}–64$
$=(\mathrm{x}–2\mathrm{y}–4)\left({\mathrm{x}}^2+4{\mathrm{y}}^2+16+2\mathrm{xy}–8\mathrm{y}+4\mathrm{x}\right)$
II. Method of splitting the middle term
This method is basically used to factorise trinomials only. Following steps are to be used during factorisation in this method.
i) We need to multiply coefficient of ${\mathrm{x}}^2$with constant term and let P be the product obtained.
ii) Split the middle term into two terms, such that their addition or subtraction results in middle term and their product is equal to P.
iii) Express the resultant polynomial into two terms by taking a common term.
Let us understand this method by (x + 3) (x + 5)
= ${\mathrm{x}}^2$ + 5x + 3x + (3 × 5)
= ${\mathrm{x}}^2$ + x (5 + 3) + (3 × 5)
= ${\mathrm{x}}^2$ + 8x + 15 ________ (1)
Thus, ${\mathrm{x}}^2$ + 8x + 15 is is obtained by multiplying
(x + 3) and (x + 5) which are its factors.
Let us check how to get the factors of ${\mathrm{x}}^2$+ 8x + 15.
From (1), we observe that, 8 is the sum of 5 and 3 and 15 is product of 5 and 3. So in order to find the factors of ${\mathrm{x}}^2$ + 8x + 15, we have to find two such numbers whose sum is 8 (i.e., coefficient of middle term) and whose product is 15 (i.e., the constant term). In order words, we have to find the factors of constant term in such a way that, when we add or subtract the factors, we get the coefficient of x.
III. Method of Completion of squares
Expressions of the form ${\mathrm{x}}^2$ + px + q may be factorised by first putting them in the form ${\mathrm{a}}^2–{\mathrm{b}}^2$.
${\mathrm{x}}^2$ + px will become a perfect square by adding the square of half of the coefficient of x i.e., ${\left(\frac{\mathrm{p}}{2}\right)}^2=\frac{{\mathrm{p}}^2}{4}.$
Let us factorise ${\mathrm{x}}^2$ + 2x – 399 using the above method.
${\mathrm{x}}^2+2\mathrm{x}–399={\mathrm{x}}^2+2\mathrm{x}+{\left(\frac{2}{2}\right)}^2–{\left(\frac{2}{2}\right)}^2–399$
$={\mathrm{x}}^2+2\mathrm{x}+1–1–399$
$=(\mathrm{x}+1{)}^2–(20{)}^2=(\mathrm{x}+1–20)(\mathrm{x}+1+20)$
$=(\mathrm{x}–19)(\mathrm{x}+21)$
IV. Grouping of terms
Expressions which can be put in the form ${\mathrm{a}}^2–{\mathrm{b}}^2$can be factorised by grouping of terms.
For example, ${\mathrm{a}}^2+\mathrm{ac}+\mathrm{bc}–{\mathrm{b}}^2$ can be factorised as follows:
The expression can be rewritten as,
${\mathrm{a}}^2–{\mathrm{b}}^2$ + c (a + b) = (a + b)(a – b) + c(a + b)
= (a + b) (a – b + c)
An expression may be resolved into factors if the terms can be arranged in groups which have a compound factor common.
2.11 HCF and LCM of Polynomials
I. HCF of Polynomials
A polynomial d(x) is said to be a divisor of a polynomial p(x), if d(x) is a factor of p(x) ie., p(x) can be written as p(x) = d(x) . q(x), where q(x) is a polynomial.
Therefore, HCF of two polynomials p(x) and q(x) is that common factor which has the highest degree among all common factors and which has the highest degree term coefficient as positive.
Let us find the HCF of the polynomials
$\mathrm{p}\left(\mathrm{x}\right)={\mathrm{x}}^2–3\mathrm{x}+2\text{ and }\mathrm{q}\left(\mathrm{x}\right)={\mathrm{x}}^2–4\mathrm{x}+4$
$\mathrm{p}\left(\mathrm{x}\right)={\mathrm{x}}^2–3\mathrm{x}+2={\mathrm{x}}^2–2\mathrm{x}–\mathrm{x}+2$
$=\mathrm{x}(\mathrm{x}–2)–1(\mathrm{x}–2)$
$=(\mathrm{x}–2)(\mathrm{x}–1)$
$\therefore \mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}–2)(\mathrm{x}–1)$
$\mathrm{q}\left(\mathrm{x}\right)={\mathrm{x}}^2–4\mathrm{x}+4={\mathrm{x}}^2–4\mathrm{x}+(2{)}^2$
$={\mathrm{x}}^2–2\times 2\times \mathrm{x}+(2{)}^2$
$=(\mathrm{x}–2{)}^2$
HCF is that common factor which has the highest degree among all common factors.
$\therefore$The highest degree common factor = x – 2.
Hence, (x – 2) is the HCF of the given polynomials.
II. LCM of Polynomials
The LCM of two polynomials p(x) and q(x) is the polynomial of the lowest degree which has both p(x) and q(x) as divisors and whose coefficient of the higher degree term has the same sign as the sign of the coefficient of the highest degree term of the product p(x) . q(x). Let us understand the method by finding LCM of polynomials
Let us understand the method by finding LCM of polynomials $\mathrm{p}\left(\mathrm{x}\right)=3{\mathrm{x}}^2+5\mathrm{x}–2,\mathrm{q}\left(\mathrm{x}\right)=3{\mathrm{x}}^2–7\mathrm{x}+2$
$\mathrm{p}\left(\mathrm{x}\right)=3{\mathrm{x}}^2+5\mathrm{x}–2$
$=3{\mathrm{x}}^2+6\mathrm{x}–\mathrm{x}–2$
$=3 \mathrm{x}(\mathrm{x}+2)–1(\mathrm{x}+2)$
$=(3\mathrm{x}–1)(\mathrm{x}+2)$
$\mathrm{q}\left(\mathrm{x}\right)=3{\mathrm{x}}^2–7\mathrm{x}+2$
$=3{\mathrm{x}}^2–6\mathrm{x}–\mathrm{x}+2$
$=3\mathrm{x}(\mathrm{x}–2)–1(\mathrm{x}–2)$
$=(3\mathrm{x}–1)(\mathrm{x}–2)$
$\therefore$ LCM of p(x) and q(x) = (3x –1) (x + 2) (x – 2)
Relation between HCF and LCM of polynomials
If m, n are two natural numbers, we know that the product of m and n is equal to the product of their HCF and LCM i.e., mn = (HCF of m and n) (LCM of m and n)
$\Rightarrow \mathrm{LCM}\text{ of }\mathrm{m}\text{ and }\mathrm{n}=\frac{\mathrm{mn}}{\mathrm{HCF} \mathrm{of} m\text{ and }\mathrm{n}}$
If p(x) and q(x) are two polynomials, we define
LCM of p(x) and q(x) $=\frac{\mathrm{p}\left(\mathrm{x}\right)·\mathrm{q}\left(\mathrm{x}\right)}{\mathrm{HCF}\text{ of }\mathrm{p}\left(\mathrm{x}\right)\text{ and }\mathrm{q}\left(\mathrm{x}\right)}$
2.12 Square root of a Polynomial
We know that, $\sqrt{4}=\sqrt{2\times 2}\text{ or }\sqrt{(–2)\times (–2)}=2\text{ ar }–2.$
$\sqrt{625}=\pm 25,\sqrt{2025}=\pm 45\text{ etc. }$
Similarly, we can find the square root of algebraic expressions.
For example, $\sqrt{4x^4}=\sqrt{\left(2x^2\right)\left(2x^2\right)}$
or $\sqrt{\left(–2{\mathrm{x}}^2\right)\left(–2{\mathrm{x}}^2\right)}=\pm 2{\mathrm{x}}^2\left[\because \sqrt[\mathrm{n}]{\mathrm{a}}={\mathrm{a}}^{\frac{1}{\mathrm{n}}}\right]$
The above algebraic expressions are monomials. We can also find out the square root of other polynomials by various methods.
Methods of finding Square roots
We can find the square roots of algebric expressions using the following methods:
I. Inspection method
II. Division method
III. Method of undetermined coefficients.
I. Finding square roots by Inspection method (Special products)
Let us consider an algebraic expression, $25{\mathrm{x}}^2+60\mathrm{xy}+36{\mathrm{y}}^2$
This can be written as ${\left(5\mathrm{x}\right)}^2$+ 2 (5x) (6y) + ${\left(6\mathrm{y}\right)}^2$.
Observe that it is in the form of ${\mathrm{a}}^2+{\mathrm{b}}^2+2\mathrm{ab}$, where a = 5x and b = 6y.
We know that, ${\mathrm{a}}^2+{\mathrm{b}}^2 +2\mathrm{ab} = {(\mathrm{a}+\mathrm{b})}^2$.
By applying the above identity, we can write
${\left(5\mathrm{x}\right)}^2$ + 2(5x) (6y) + ${\left(6\mathrm{y}\right)}^2$ = ${\left(5\mathrm{x}+6\mathrm{y}\right)}^2$
$\therefore 25{\mathrm{x}}^2+60\mathrm{xy}+36{\mathrm{y}}^2=(5\mathrm{x}+6\mathrm{y}{)}^2$
$\therefore$ Square root of $\sqrt{25{\mathrm{x}}^2+60\mathrm{xy}+36{\mathrm{y}}^2}$
$=\sqrt{(5\mathrm{x}+6\mathrm{y}{)}^2}={\left[(5\mathrm{x}+6\mathrm{y}{)}^2\right]}^{\frac{1}{2}}=\left(5\mathrm{x}+6\mathrm{y}\right)$
$\therefore \sqrt{25{\mathrm{x}}^2+60\mathrm{xy}+36{\mathrm{y}}^2}=(5\mathrm{x}+6\mathrm{y})$
II. Finding square root by Division method
Let us find the square root of $–2\mathrm{x}+3{\mathrm{x}}^2+{\mathrm{x}}^4–2{\mathrm{x}}^3+1$ by using division method.
Step – 1: Given expression is to be arranged in the descending powers of x i.e., ${\mathrm{x}}^4–2{\mathrm{x}}^3+3{\mathrm{x}}^2–2\mathrm{x}+1$
Step – 2: Find the square root of the first term of the given expression  ${\mathrm{x}}^4 . \sqrt{{\mathrm{x}}^4}={\mathrm{x}}^2$
Write ${\mathrm{x}}^2$ in the place of divisor and quotient.
Multiply the divisor and quotient i.e., ${\mathrm{x}}^2\times {\mathrm{x}}^2={\mathrm{x}}^4$.
Write the product below ${\mathrm{x}}^4$.
Subtract them and get 0 as remainder.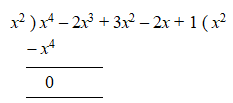

Let us continue the division.
The next two terms in the expression $–2{\mathrm{x}}^3+3{\mathrm{x}}^2$ are to be brought down as the divided for the next step.
Step – 3: Double the first term of quotient and divide the first term of the second divisor $–2{\mathrm{x}}^3$ by $2{\mathrm{x}}^2$.
$\frac{–2{\mathrm{x}}^3}{2{\mathrm{x}}^2}=–\mathrm{x}$

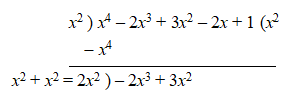
Continue the division and –x is the second term for quotient and second divisor.
Step – 4: Multiply the second divisor with second term of the quotient i.e., –x and write the product below $–2{\mathrm{x}}^3+3{\mathrm{x}}^2$ and get the remainder $2{\mathrm{x}}^2$ by subtracting them.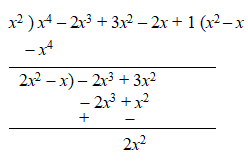

Continue the division and bring the next two terms (–2x + 1) in the expression as the dividend for the next step.
$\left(2{\mathrm{x}}^2\right)\Rightarrow \frac{2{\mathrm{x}}^2}{2{\mathrm{x}}^2}=1$
Step – 5: Write + 1 as third term of quotient and third divisor. Multiply the third divisor.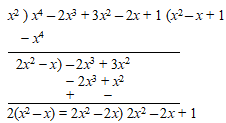

Multiply the third divisor 2${\mathrm{x}}^2$ – 2x + 1 with third term of quotient i.e., 1 and write the product below the dividend 2${\mathrm{x}}^2$ – 2x + 1. Subtract them, to get 0 as remainder.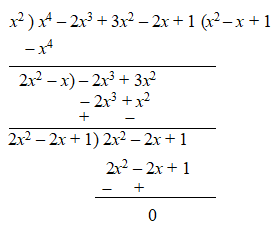

The quotient (${\mathrm{x}}^2$ – x + 1) thus obtained is the square root of ${\mathrm{x}}^4–2{\mathrm{x}}^3+3{\mathrm{x}}^2–2\mathrm{x}+1$.
$\therefore \sqrt{{\mathrm{x}}^4–2{\mathrm{x}}^3+3{\mathrm{x}}^2–2\mathrm{x}+1}=\left({\mathrm{x}}^2–\mathrm{x}+1\right)$
III. Finding square roots by Undetermined Coefficients Method:
Let us understand the steps by finding the square root of ${\mathrm{x}}^4+4{\mathrm{x}}^2+4$.
Step – 1 : Check the degree of the given expression. Here, degree of the polynomial = 4
Step – 2: Find a polynomial of degree half the degree of the given expression.
Polynomial of degree = 4/2 = 2
$\therefore$ a${\mathrm{x}}^2$ + bx + c is the required polynomial
Perfect square
An expression that can be written as a product of two equal factors is called a perfect square.
For example, let us show that the following, is a perfect square (x + 1) (x + 2) (x + 3) (x + 4) + 1
(x + 1) (x + 4) (x + 2) (x + 3) + 1
= (${\mathrm{x}}^2$ + 5x + 4) (x2 + 5x + 6) + 1
Let ${\mathrm{x}}^2$ + 5x be a
Therefore, the given expression becomes ,
${\mathrm{a}}^2+10\mathrm{a}+25=(\mathrm{a}{)}^2+2\left(5\right)\left(a\right)+(5{)}^2=(\mathrm{a}+5{)}^2$
$={\left({\mathrm{x}}^2+5\mathrm{x}+5\right)}^2$
i.e., the given expression is written as two equal factors like $\left({\mathrm{x}}^2+5\mathrm{x}+5\right),\left({\mathrm{x}}^2+5\mathrm{x}+5\right)$.
$\therefore$ (x + 1) (x + 2) (x + 3) (x + 4) + 1 is a perfect square.
2.13 Other types of Algebraic expressions
I. Homogeneous Expressions
If the sum of powers of variables in all the terms of an expression is the same, the expression is called Homogeneous Expression.
For example, $3{\mathrm{x}}^4+{\mathrm{x}}^2{\mathrm{y}}^2+2{\mathrm{y}}^4$ is a homogeneous expression as the sum of powers of variables in all terms is the same.
Standard form of Homogeneous Expressions

II. Symmetric Expressions
An expression f(x, y) is said to be symmetric, if f(x, y) = f(y, x) i.e., the expression does not change, when variables are interchanged.
Example: $\mathrm{f}(\mathrm{x},\mathrm{y})=4{\mathrm{x}}^2+2{\mathrm{x}}^2\mathrm{y}+2{\mathrm{xy}}^2+4{\mathrm{y}}^2$
After interchanging variables,
$\mathrm{f}(\mathrm{y},\mathrm{x})=4{\mathrm{y}}^2+2{\mathrm{y}}^2\mathrm{x}+2{\mathrm{yx}}^2+4{\mathrm{x}}^2$
$=4{\mathrm{x}}^2+2{\mathrm{x}}^2\mathrm{y}+2{\mathrm{xy}}^2+4{\mathrm{y}}^2$
$=\mathrm{f}(\mathrm{x},\mathrm{y})$
III. Cyclic Expressions
An expression f(x, y, z) is said to be “cyclic” if the expression obtained by replacing x with y, y with z, z with x which is f(y, z, x) is the same as given expression f(x, y, z) i.e., f(x, y, z) = f(y, z, x). Such an expression is called cyclic expression.
Example: $\mathrm{f}(\mathrm{x},\mathrm{y},\mathrm{z})={\mathrm{x}}^3(\mathrm{y}–\mathrm{z})+{\mathrm{y}}^3(\mathrm{z}–\mathrm{x})+{\mathrm{z}}^3(\mathrm{x}–\mathrm{y})$
$\mathrm{f}(\mathrm{y},\mathrm{z},\mathrm{x})={\mathrm{y}}^3(\mathrm{z}–\mathrm{x})+{\mathrm{z}}^3(\mathrm{x}–\mathrm{y})+{\mathrm{x}}^3(\mathrm{y}–\mathrm{z})$
$={\mathrm{x}}^3(\mathrm{y}–\mathrm{z})+{\mathrm{y}}^3(\mathrm{z}–\mathrm{x})+{\mathrm{z}}^3(\mathrm{x}–\mathrm{y})$
which is same as f(x, y, z). Such expressions are called cyclic expressions.
Note:For any expression to be cyclic, it should have a minimum of three variables.