3.1 Introduction
Coordinate geometry is a method of studying geometry with the help of Algebra.
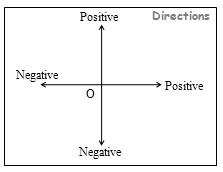
Here we represent any point in a plane by its distances from two fixed perpendicular lines. The horizontal line is called the x-axis and the vertical line is called the y-axis. These two lines together are called the coordinate axes. The point of intersection of these lines is called the origin ‘O’, as shown
3.2 Cartesian System
Coordinate Axes
The position of a point in a plane is determined with reference to the intersecting straight lines called coordinate axes. Their point of intersection is called the origin of coordinates. If these two axes of reference cut each other at right angles, they are called rectangular axes. Otherwise, they are called oblique axes.
x coordinate
It is the distance between y-axis and the point ‘P’ which is measured in the direction of x-axis. In the adjacent diagram, the distance between y-axis and the point p in the direction of x-axis is BP.
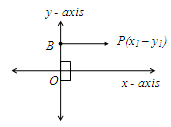
The x coordinate of P = BP =
Note: x coordinate is also called abscissa.
y coordinate
It is the distance between x-axis and the point ‘P’ which is measured in direction y-axis.
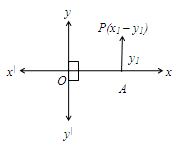
In the above diagram the distance between x-axis and the point p in the direction of y-axis is AP.
The y coordinate of P = AP =
Note: y coordinate is also called ordinate.
Quadrants
x and y axes divide the plane into four quadrants and each axis has two directions.
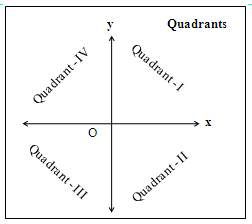
Signs of x and y-axes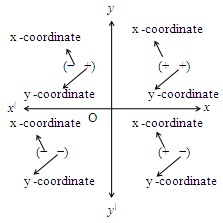
3.3. Plotting a Point in the Plane if its Coordinates are given
A point on x-axis
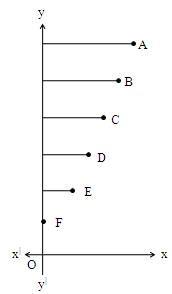
Observe the adjacent figure: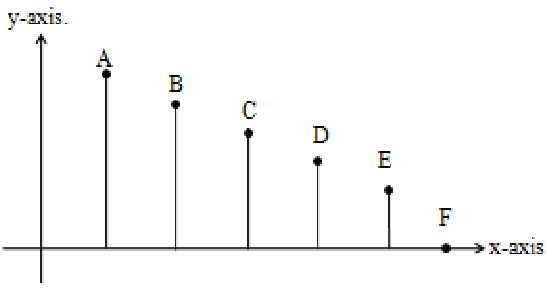
It is clear that the distance from the points A, B, C, D, E, F to x-axis is gradually decreasing.
Finally, the point ‘F’ is on the x-axis.
i.e., its distance from x-axis becomes zero.
What is this point ‘F’ called ?
A point which is on x-axis and whose y co-ordinate is zero is called “a point on x-axis”.
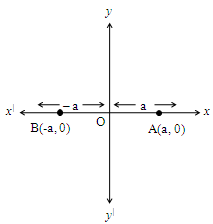
In general, any point on x-axis is represented as (± a, 0) where ‘a’ is the distance between the point and y-axis as shown below.
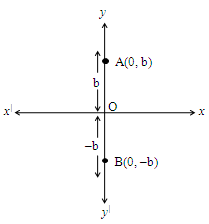
A point on y-axis
It is clear that the distance from the points A, B, C, D, E, F to y-axis is gradually decreasing.
Finally, the point ‘F’ is on the y-axis i.e., its distance from y-axis becomes zero.
What is this point ‘F’ called ?
A point which is on y-axis and whose x co-ordinate is zero is called “a point on y-axis”.
In general, any point on y-axis represented as (0, ±b) where ‘b’ is the distance between the point and x-axis, as shown in the adjacent figure.
Points on the Angular Bisector of axes
Let’s observe the following:
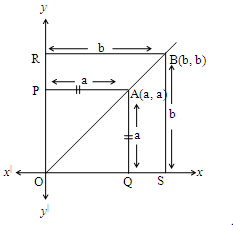
It is clear that point ‘A’ lies on the bisector of x & y axes.
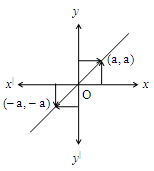
The point ‘A’ is equidistant from x & y axes.
i.e., A P = x co-ordinate = a
A Q = y co-ordinate = a
What can we conclude ?
All the points on the bisector have their x coordinates = y coordinates.
NOTE:
i) Any point on the bisector of x and y axes through I and III quadrants are of the form (a, a) and (–a,–a) respectively.
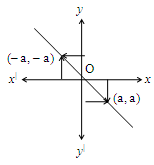
i) Any point on the bisector of x and y axes through II and IV quadrants are of the form (– a, a) and (a, a) respectively.
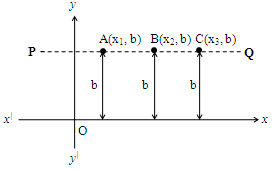
Points on the line parallel to y-axis
Observe the adjacent figure.
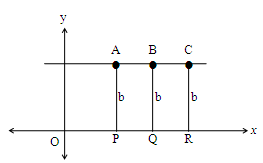
It is clear that points A, B and C on a line parallel to x-axis and are equidistant from x-axis
i.e., AP = BQ = CR = b units
NOTE:
i) For the points lying on the line parallel to x-axis, their distances from x-axis are same i.e. their
y-coordinate are same. In the above diagram, y coordinate of all the point is b.
ii) Any point on a line parallel to x-axis is of the form (x, b), where ‘b’ is the distance between the point and x-axis.
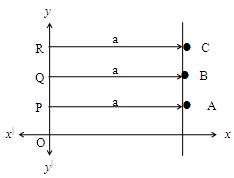
Observe the adjacent figure.
It is clear that points A, B and C on a line parallel to y-axis are equidistant from y-axis.
i.e., AP = BQ = CR = a units.
NOTE:
i) For the points lying on the line parallel to y-axis, their distances from y-axis are same i.e. their x coordinates are same.
ii) Any point on a line parallel to y-axis is of the form (a, y), where ‘a’ is the distance between the point and x-axis.
Test yourself by Matching
Let’s match the following points with its correct location.
|
Points |
Location |
|
i) (–4, 0) ii) (–5,5) iii) (0,–6) iv) (7,7) v) (5, 6), (5,–2) (5, 7) vi) (1, 2), (2, 2) (6, 2) |
Line parallel to x-axis b) x-axis c) y-axis d) Bisector through I & III quadrants e) Bisector through II & IV quadrants f) Line parallel to y-axis. |
i) (– 4, 0) will be on “ y-axis”.
ii) (– 5, 5) will be on the “bisector through II & IV quadrants”
iii) (0, – 6) will be on “ y-axis”
iv) (7, 7) will be on the “ bisector through I & III quadrants”
v) {(5, 6), (5, – 2) (5, 7)} will be on the “line parallel y-axis”
vi) {(1, 2), (2, 2) (6, 2)} will be on the “ line parallel to x-axis”.
3.4 Distance between two points
Observe the adjacent figure.
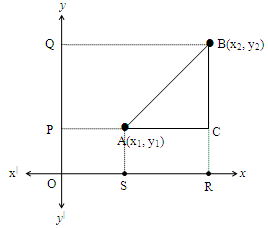
From the definitions of x and y coordinates,
PA = and QB =
AS = and BR =
In ABC,
AC = PC – PA. = QB – PA ( PC = QB)
= –
BC = BR – CR
= BR – AS ( AS = CR)
= –
Applying Pythagoras theorem to ABC, we get:
= +
= +
Distance between two points A(, ) and B(, )
It is also written as:
Example
Let’s find the distance between two points; A(2, – 3), B(5, 4)
Let (, ) = (2, – 3); (, ) = (5, 4)
We have AB
The distance between A(2, – 3) and B(5, 4) is
3.5 Four sided Figures
Type-I
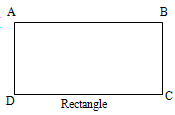
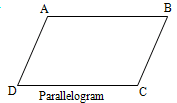
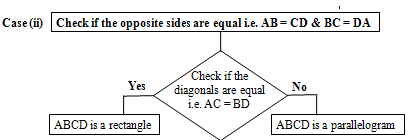
Opposite sides are equal , i.e., AB = CD & BC = AD.
Then the figures can be a rectangle or parallelogram:
NOTE
The difference between the two is that in rectangle the diagonals (AC = BD) are equal, whereas in a parallelogram they are not equal.
Type-II
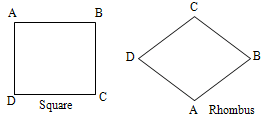
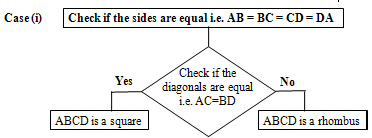
All sides are equal i.e., AB = BC = CD = AD.
Then the figures can be a square or rhombus:
NOTE
The difference between a square and a Rhombus is that in a square the of diagonals AC = BD, are equal, whereas in a Rhombus the diagonals are not equal.
Type-III
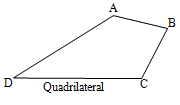
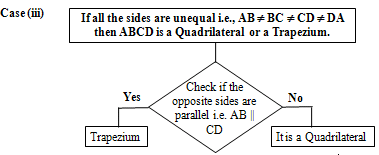
The four sides are unequal, i.e., AB BC CD AD,
Then the figures can be a quadrilateral or a trapezium:
NOTE
i) The difference between a quadrilateral and a trapezium is that a trapezium has two parallel sides.
ii) In an isosceles trapezium, the non-parallel sides are equal.
Nature of four-sided figures – Cases
3.6 Equation of a Straight Line
Let AB be a line segment;
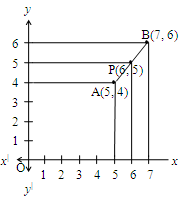
A(5, 4) and B(7, 6) are two points on it.
Let P be the midpoint of AB.
Since ‘P’ is the midpoint of AB,
The x coordinate of midpoint ‘P’ will be taken as the mean of x coordinates of points A and B.
The same thing holds good for y coordinate of midpoint p.
Coordinates of mid – point p are
In general, the coordinates of midpoint of a line segment which joins A(, ) and B(, ) are
Let’s observe the following
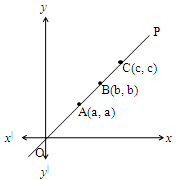
It is clear that
x coordinate () of A = y coordinate () of A. = a
x coordinate () of B = y coordinate () of B. = b
x coordinate () of C = y coordinate () of C. = c
So, the bisector of coordinate axes passing through I & III quadrants.
It can be generalized as x coordinate = y coordinate
x = y
What is this relation between x and y coordinates called?
The generalized relation between x and y coordinates of points on a line is known as Equation of a line. i.e. The equation of bisector passing through the I and III quadrants is x = y or x – y = 0.
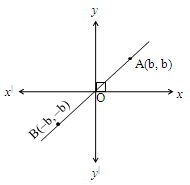
Equations of Some Special lines
Observe the adjacent figure.
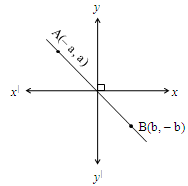
It is clear that x coordinate of A and B not equal to coordinates of A and B
So also the bisector of coordinate axes passing through II & IV quadrants.
It is observed that y coordinate of any point is equal and opposite to the x coordinate of the same point.
i.e., it can be generalized as y = – x
So the equation of bisector is y = – x or x + y = 0
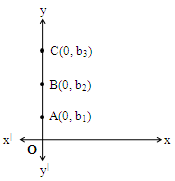
Equation of x-axis:
All points on x-axis have their y coordinates equal to zero.
This can be generalized as y = 0.
i.e. the equation of x-axis is y = 0.
Equation of y-axis:
All points on y-axis have their x coordinates equal to zero.
This can be generalized as x = 0. i.e. the equation of y-axis is x = 0.
Equations of line parallel to x-axis
We have two cases here; they are:
i) Line parallel to x-axis and above it
ii) Line parallel to x-axis and below it.
Case- I : Equation of a line parallel to x – axis above it
Observe the adjacent figure.
Let A, B and C be the points on the line PQ parallel to x-axis and above it. It is observed that the
y-coordinates of these points is ‘b’.
This can be generalized as y = b.
i.e., the equation of the line parallel to x-axis and above it is y = b.
Case – II: Equation of a line parallel to x – axis below it
Observe the adjacent figure. Let D, E and F be the points on the line PQ parallel to x-axis and above it.
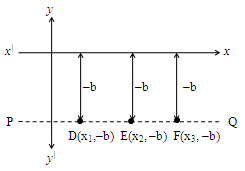
It is observed that the y coordinate of these points is ‘–b’. This can be generalized as y = –b.
i.e., the equation of the line parallel to x-axis and below it is y = –b.
Equation of line parallel to y-axis
We have two cases they are:
i) Line parallel to y-axis on the right side.
ii) Line parallel to y-axis on the left side.
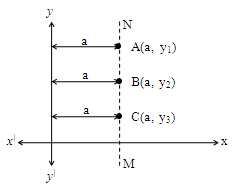
Case – I: Equation of a line parallel to y – axis on the right side
Let A, B and C be the points on the line MN parallel to y-axis on the right side. It is observed that
x-coordinates of these points is ‘a’. This can be generalized as x = a. i.e., the equation of the line parallel to y-axis on the right side (I quadrant) is x = a
Case – I: Equation of a line parallel to y – axis on the left side
Observe the adjacent figure following:
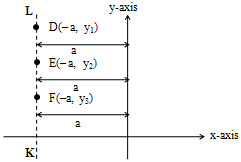
Let D, E and F be the points on the line KL parallel to y-axis on the left side. It is observed that x coordinates of these points is ‘– a’. This can be generalized as x = –a.
i.e., the equation of the line parallel to y-axis on the left side (II quadrant) is x = –a or x + a = 0
Reflection of the lines parallel to x-axis
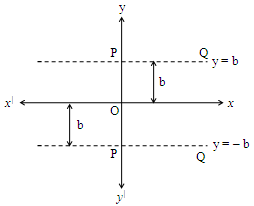
Let’s imagine that a plane mirror is placed along the x-axis. The reflection of the line ‘PQ’ appears below the x-axis which is at same distance from x-axis, as shown in the figure.
The equation of the reflected line is y = – b.
Reflection of the lines parallel to y-axis
Let’s imagine that a plane mirror is placed along the y-axis. The reflection of the line ‘RS’, appears on the left side of the y-axis, which is at same distance as ‘RS’ from y-axis, as shown in the figure.
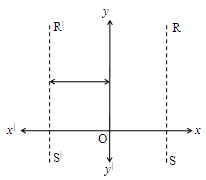
The equation of the reflected line is x = – a or x + a = 0
General equation of a line segment
General equation of a line is ax + by + c = 0
For any point on the line the following condition is satisfied:
(a times its x coordinate) + (b times its y coordinate) + c = 0.
Example : 5x – 2y + 3 = 0.
Note
i) ax + by + c = 0 is a linear equation which represents a straight line.
ii) The point which lies on the straight line satisfies the equation.
Example
Let’s verify whether point (2, 3) lies on the line
2x – 3y + 5 = 0 or not. 2(2) – 3(3) + 5 = 0
4 – 9 + 5 = 0
The point (2, 3) lies on 2x – 3y + 5 = 0.
3.7 Slope of a Straight Line
Each straight line has a particular direction, and this direction is understood by the quantity called slope.
Slope is usually denoted by m.
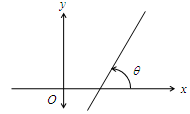
m = tan (where ‘’ is the angle between straight line & x-axis).
Formulae for slope:
i) Slope of a straight line, given its equation ax + by + c = 0
ii) Slope of a straight line, given two points (, ) and (, ) on it.
Slope of x-axis
Let A and B be the two points on x-axis, as shown in the figure.
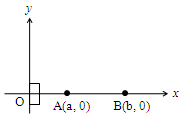
Points are A(a, 0) and B(b, 0),
We have = a; = 0; = b; = 0.
Slope of x-axis = 0
Slope of y-axis
Let A and B be the two points on y-axis, as shown in the figure.
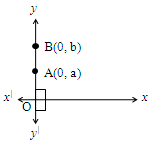
The points are A(0, a) and B(0, b)
= 0; = a; = 0; = b.
Slope of y-axis =
Slope of a line parallel to x-axis
Let A and B be the two points on a line parallel to x-axis as shown in the figure.
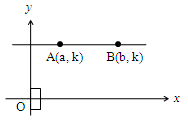
The points are A(a, k) and B(b, k). = a; = k; = b; = k.
Slope of a line parallel to x-axis = 0
Slope of a line parallel to y-axis
Let A and B be the two points on a line parallel to y-axis as shown below. The points are A(k, a) and B(k, b).
= k; = a; = k; = b.
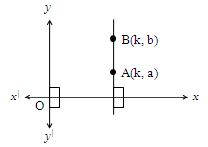
Slope of a line parallel to y-axis =
Slope of Bisector Through I and III quadrants
Let A and B be the two points on bisector through I and III quadrants as shown in the figure.
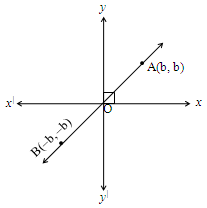
The points are A(a, a) and B(b, b).
= a; = a; = b; = b.
Slope of a bisector through I and III quadrants is 1.
Slope of Bisector through II and IV quadrants
Let A and B be the two points on bisector through II and IV quadrants as shown below.
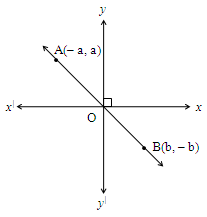
The points are A(– a, a) and B(b, – b).
= – a; = a; = b; = – b.
The slope of a bisector through II and IV quadrants is –1
Slope of special lines – Summary
|
SLOPE OF SPECIAL LINES – SUMMARY |
|||
|
S.No. |
Special Line |
Equation |
Slope |
|
1 |
x-axis |
y = 0 |
0 |
|
2 |
y-axis |
x = 0 |
|
|
3 |
Line parallel to x-axis |
yk |
0 |
|
4 |
Line parallel to y-axis |
x = k |
|
|
5 |
Bisector of the angle between coordinate axes (I and III quadrants) |
x y = 0 |
+1 |
|
6 |
Bisector of the angle between coordinate axes (II and IV quadrants) |
x + y = 0 |
+1 |
3.8 Condition of two Straight Lines
Let’s see some conditions for two straight lines:
i) to be parallel
ii) to be perpendicular.
Condition for two straight lines to be Parallel
Let and be two straight lines, making angles and with x-axis as shown in the adjacent figure.
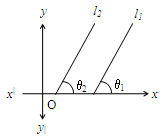
What do we call these two lines if = ?
Let’s take ‘tan’ on both the sides:
i.e., tan = tan =
i.e., we call these two lines parallel lines
NOTE
i) It two lines are parallel, their slopes are equal.
ii) As slopes are equal for parallel lines, they are of the form ax + by = c, where c is a variable.
Condition for two straight lines to be Perpendicular
Let and be two straight lines, making angles and with x-axis as shown below.
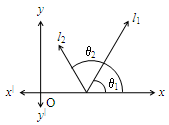
What do we call these two lines if = 90 + ?
Let’s take ‘tan’ on both the sides:
tan = tan (90 + )
= – 1
i.e., we call these two lines perpendicular lines
NOTE
i) If two lines are perpendicular, the product of their slopes is equal to ‘–1’.
ii) Two lines of the form ax + by = and bx – ay = are perpendicular, as the product of their slopes is equal to ‘– 1’.
3.9 Intercept Form
Let us observe the following:
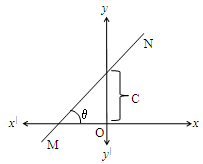
It is observed that
the straight line MN intersect x and y axes
MN makes y-intercept ‘c’.
This can be generalized as y = mx + c.
Where m = slope
c = y-intercept.
NOTE:
i) The point at which a line/curve intersects an axis is known as an intercept.
ii) The x-intercept is the point where the curve crosses the x-axis. y-intercept is the point where the curve crosses the y-axis.
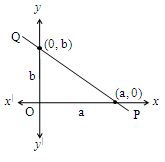
Now, observe the following:
It is observed that:
PQ is a straight line inters seating x and y-axes at (a, 0), (0, b) on respectively
i.e., x-intercept = a
y-intercept = b
The equation is where a x-intercept
a y-intercept
Slope point form
Observe the following:
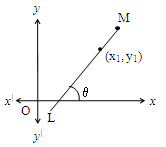
It is observed that:
LM is a straight line making an angle with x-axis.
i.e., m = tan
where ‘m’ is a slope of (, )
The equation is y – = m (x – )
Two-point formula
Observe the adjacent figure.
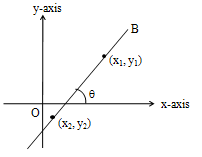
It is observed that:
AB is a straight line having points (, ) and (, ) on it and making an angle ‘’ with x-axis
The equation is
Various forms of equation – summary
|
S.No. |
Name |
Equation |
TWO conditions |
|
1 |
Slope intercept form |
m slope and c constant |
|
|
2 |
Intercept form |
a x-intercept, b y intercept |
|
|
3 |
Slope point form |
m,(, ) a point on die line. |
|
|
4 |
Two-point form |
(, ) and (, ) a re points on die line |
Equation of a Straight line through (, ) and parallel to ax + by + c = 0
Let ax + by + c = 0 __________ (i) be a straight line.
Slope of (i)
Since slopes are equal for parallel lines,
The slope of the required line parallel to (i)
Lines with slope of have equation of the form
ax + by = k _______ (ii)
( slope of ax + by + k is ).
If the straight line passes through (, ), then
k = a + b
On substituting the k value in the equation (ii), we get ax + by = (a + b)
ax + by – (a + b) = 0
The equation of a straight line through (, ) and parallel to ax + by + c = 0 is
ax + by – (a + b) = 0
Equation of a straight line through (, ) and perpendicular to ax + by + c = 0
Let ax + by + c = 0 _________ (i) be a straight line.
Slope of (i) =
Since the product of the slopes of perpendicular lines is equal to ‘–1’. the slope of a straight line perpendicular to (i) is equal to
Hence the equation of the straight line perpendicular to (i) will be in the form bx – ay = k ____ (ii)
If the straight line passes through
on substituting the ‘k’ value in the equation (ii), we get
The equation of a straight line through and perpendicular to ax + by + c = 0 is








