5.1 Basic Terms and Definitions
Point
A point is represented by a dot. It has no dimensions like length, breadth or thickness. It has only position. Points are denoted by capital letters A, B, C, D, P, Q, R etc. A point ‘A’ is represented as A. For example, a dot made by a sharp pencil is a point.
Line
A geometrical line is a set of points that extends endlessly in both the directions. i.e., a line has no end points. It has only length. The arrowheads show that the line goes on endlessly on either side.
A line is also called a straight line. The line AB is represented as . Another kind of line is a curved line.

For example, the edge of a ruler extending endlessly in both the directions. Lines are denoted by small letters , m, n, …. etc.
Line–segment
A line-segment is a line which has end points. In the above figure, the part of the line between the points A and B, including A and B, is a line-segment.
![]()
The line – segment AB is represented as or segment AB.
Plane
A plane is a set of points. It is a flat surface with length and breadth.
A geometrical plane extends endlessly in all the directions. Small letters are used to denote a plane. For example, the surface of a sheet of paper, surface of a wall and Surface of a matchbox.
Coplanar Points
The points that belong to the same plane are called coplanar points.
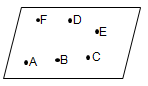
In the above figure, the points A, B, C, D, E and F are coplanar points.
Coplanar Lines
The lines that lie in the same plane are called coplanar lines.
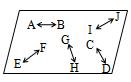
In the above figure, the lines AB, CD, EF, GH and IJ are coplanar lines.
Space
The universal set of points, lines and planes is called a space. It has no end.
Points and Lines Incidence Properties
The relation between a point and a line is called an incidence property.
Let us consider a line ‘’ and a point ‘p’. If p , then we say that ‘p’ is incident on ‘’. The line ‘’ passes through the point ‘p’.
Distance between two Points
The distance between two points A and B is the length of the line–segment joining them. The distance between A and B is denoted by d(A, B) or AB.
Midpoint
Given a line–segment AB, a point M is said to be the midpoint of AB, if M is an interior point of AB, such that AM = MB.
Perpendicular bisector of a Line–Segment
A line ‘’ passing through the midpoint ‘M’ of a line–segment and perpendicular to AB is called the perpendicular bisector of the line–segment
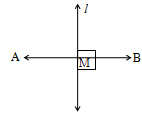
Collinear Points
If three or more points lie on a straight line, then those points are called collinear points.![]()
A, B, C, D and E are collinear points.
Non-collinear Points
The points which do not lie on the straight line are called non-collinear points.

In the above figure, the points ‘C’, ‘G’, ‘H’ do not lie on the straight ‘l’. Hence they are non-collinear points.
A point ‘C’ is said to lie between ‘A’ and ‘B’, if
a) A, B, C are collinear and
b) AB = AC + CB.
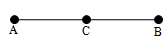
Ray
Let ‘’ be a line and A, B be two distinct points on ‘’.
A ray is a part of the line ‘’ which has one end point at ‘A’ and contains the point ‘B”. A ray is denoted by the symbol
![]()
Opposite Rays
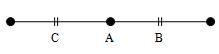
Consider two rays and . The two rays and are said to be opposite rays, if they are collinear and , ,i.e., the point A is the only common point of the two rays.
5.2 Properties of Straight Lines
1. On a single line , there exists infinite number of points.
2. An infinite number of lines pass through a single point P. (concurrent lines)
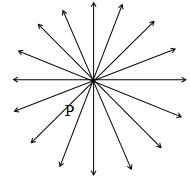
3. Only a single line passes through two distinct points A and B.

4. Given two different lines ‘’ and ‘m’, there exists only one point ‘p’, which lies on both the lines ‘’ and ‘m’.
i.e., the two lines intersect at P.
Note: Two distinct lines cannot have more than one common point
5.3 Intersecting Lines and Non-intersecting Lines
Parallel Lines
The lines which do not intersect each other when produced? and do not have any point in common are called parallel lines.

The lines ‘’ and ‘m’ are parallel lines.
Parallel lines are denoted as ‘||’.
Concurrent Lines
When three or more lines pass through a single point, they are called concurrent lines.
In the above figure the lines k, , m and n are concurrent lines. Two rays or two line–segments or a ray and a line–segment are said to be parallel if the lines containing them are parallel.
Transversal
A line which intersects two or more lines at distinct points is called a transversal of the given lines.
In the figure, AB is the transversal to the lines CD and EF.
Degree
If the line–segment AO rotates about ‘O’ through a complete rotation, it comes back to its original position.
This complete rotation is divided into 360 equal parts. Each part is called a degree and is denoted as ‘°’.
Measure
In the given figure, the line-segments AO and BO meet at O; O is the vertex of the AOB and AO and BO are called the measure of AOB. It is denoted as m AOB.
For example, in the given figure, if the measure of the AOB is x°, then we write m AOB = x°.
Minutes and Seconds
Each degree is divided in to 60 equal parts called minutes.
Symbolically 1° = .
Each minute is divided into 60 equal parts called seconds.
Symbolically = .
1° = = 60 × = .
Thus one degree is equal to 3600 seconds.
5.4 Angle
An angle is the union of two rays with a common initial point. When a ray AB rotates in the plane about the point A and takes a new position AC, an angle BAC is formed. The Symbol of angle is
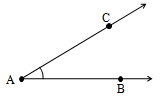
The angle formed by the two rays and is denoted by BCA or CAB. The two rays and are called the arms, and the common initial point A is called the vertex.
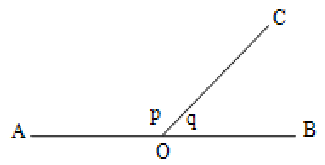
Bisector of an angle
A line which divides an angle into two equal parts is called the Bisector of the angle.
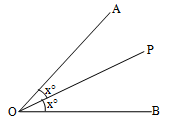
Example
In the figure below, the line OP divides AOB into two equal parts i.e., ?AOP = ?POB = x°
The line OP is called the bisector of AOB.
5.5 Types of Angles
There are six types of angles. They are:
i) Acute Angle
ii) Right Angle
iii) Obtuse Angle
iv) Straight Angle
v) Reflex Angle
vi) Complete Angle
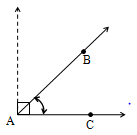
Acute Angle
An angle which is less than 90° is called an acute angle.
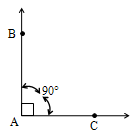
Right Angle
An angle which is equal to 90° is called a right angle.
Obtuse Angle
An angle which is greater than 90° but less than 180° is called an obtuse angle.
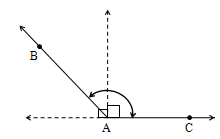
Straight Angle
An angle which is equal to 180° is called a straight angle.
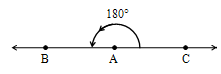
Reflex Angle
An angle which is greater than 180° but less than 360° is called a reflex angle.
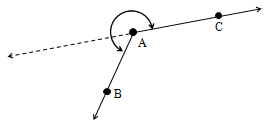
Note: An angle is said to be a zero angle when two rays coincide and the measure is 0°.
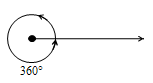
Complete Angle
An angle which is exactly equal to 360° is called a complete angle.
5.6 Pair of Angles
Complementary Angles
When the sum of the measures of two angles is equal to 90°, then the angles are said to be complementary angles.
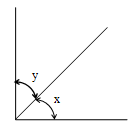
Here x + y = 90°, therefore x and y are complementary angles.
Supplementary Angles
When the sum of the measures of two angles is equal to 180°, then the angles are said to be supplementary angles.
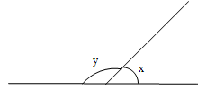
Here x + y = 180°, therefore x and y are supplementary angles.
Adjacent Angles
Angles having the same vertex and a common side, and which lie on the opposite sides of the common side are called adjacent angles.
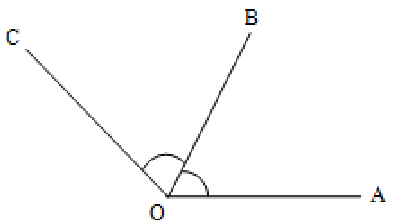
Angles AOB and COB with common vertex O and common side OB are adjacent angles.
Linear Pair of Angles
Two adjacent angles are said to form a linear pair of angles if they lie on the same straight line. The two non–common arms are opposite rays.
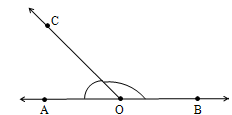
In the above figure, AOC and BOC are adjacent angles. OA and OB are the rays which are non–common arms and are collinear.
The sum of the two adjacent angles of a linear pair of angles is 180°; hence they are also supplementary.
Two adjacent angles are a linear pair of angles if, and only if, they are supplementary.
Note: If p + q = 180°, then AB is a straight line.
Perpendicular Lines
Any two straight lines lying in the same plane, that meet each other at right angles are called perpendicular lines. Perpendicular lines are denoted by the symbol .
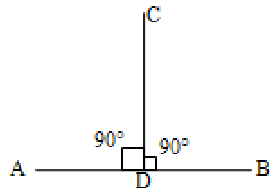
Let AB be a straight line and CD be a line on AB such that BDC = CDA = 90°; then we say that CD AB.
Congruent Angles and An axiom
Two congruent angles have the same measure and, conversely, two angles of equal measure are congruent.
Consider two angles, ABC and DEF.
If the two angles are congruent, then we write
ABC DEF
Vertically Opposite Angles
If two lines AB and CD intersect at a point O, then the pair of angles AOC and BOD is said to be a pair of vertically opposite angles. Vertically opposite angles (also vertical angles) are those which have a common vertex and the sides of one are the extended sides of the other. OA and OB are opposite rays. OC and OD are also opposite rays.
Also AOD and BOC form another pair of vertically opposite angles.
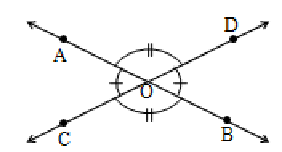
Note: Two angles are said to be a pair of vertically opposite angles if their arms form two pairs of vertically opposite rays .
Angles forming a pair of vertically opposite angles are congruent (or equal).
Position of points with respect to Angle
Interior of an Angle
The interior of an angle is the set of all points P in its plane, which lie on the same side of line AB as C and also on the same side of line AC as B.
Angle addition Axiom
If P is an interior point of any angle ABC, then m ABC = m ABP + m PBC
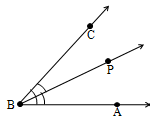
Exterior of an Angle
The exterior of an angle is the set of all points Q in its plane, which do not lie on the angle or in its interior.
Angles around a Point
When a number of lines meet at a single point, they form angles around that point.
The sum of the measures of all these angles formed around the point is equal to 360° i.e., four right angles are formed.
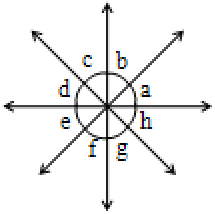
i.e., measures of
(a + b + c + d + e + f + g +h) = 360°
ma + mb + mc + md + me + mf + mg + mh = 360°
The sum of the angles around a point is 360°.
5.7 Parallel Lines and a Transversal
When a transversal AB intersects two lines CD and EF at two distinct points G and H, then the three lines determine eight angles, four angles at point G, and four angles at point H.
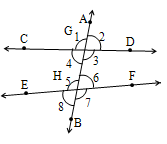
The angles at the point G are 1,2, 3 and 4 and the angles at the point H are 5, 6, 7 and 8.
Interior Angles
Angles inside the parallel lines and on both sides of the transversal are called interior angles. The angles 3, 4, 5 and 6 are called interior angles.
Co-interior Angles
Two angles are said to be co-interior angles or interior opposite angles if they are interior angles and lie on the same side of the transversal. In the above figure, the following pairs of angles are co-interior angles:
i)3 and 6
ii) 4 and 5
Exterior Angles
Angles lined outside the parallel lines on both sides of the transversal are called exterior angles.
Corresponding Angles
Two angles are said to be a pair of corresponding angles if they are on the same side of the transversal with one angle interior and the other angle exterior and the angles are not adjacent angles.
Axiom of corresponding Angles
If a transversal intersects two coplanar parallel lines, then the corresponding angles are equal. Conversely, if the a transversal intersects two coplanar lines, making a pair of corresponding angles equal, then the lines are parallel.
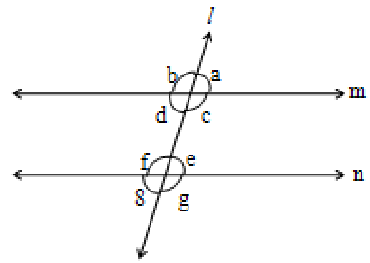
In the above figure ‘l’ is the transversal intersecting the parallel lines ‘m’ and ‘n’. Then the following pairs of corresponding angles are equal.
i) a = e ii) b = f
iii) c = g and iv) d = h
Alternate Angles
Two angles are said to be a pair of alternate angles if the angles are interior angles, which lie on either side of the transversal and are not adjacent angles.
In the above figure, the pairs of alternate angles formed are
(i) d and e
(ii) c and f.
Results of a Transversal Intersecting Parallel Lines
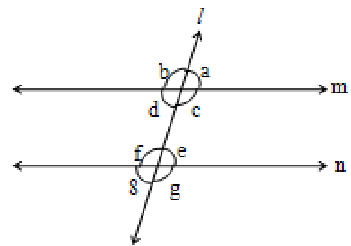
i) When a transversal intersects two parallel lines, eight angles are formed.
ii) The sum of the four interior angles is 360°.
iii) The sum of the co-interior angles is 180°.
iv) The sum of the four exterior angles is 360°.
v) The alternate angles are equal.
vi) The corresponding angles are equal.
vii) If two lines are cut by a transversal such that two corresponding angles are equal, then the two lines are parallel.
viii) If two lines are cut by a transversal such that two alternate angles are equal, then he two lines are parallel.
ix) Alternate exterior angles are equal. In the figure and , and are alternate exterior angles.
x) The sum of the exterior angles that are on the same side of the transversal is 180°.
5.8 Basic Theorems on Angles
Proof: Consider a straight line AB.
Let the straight line OC make the adjacent angles AOC and COB with this line.
It is required to prove that AOC and COB are together equal to 180°.
Suppose OD is perpendicular to AB.
i.e., OD is at right angles to AB.
Then, AOC + COB
= AOC + COD + DOB –––––––– (1)
Also, AOD + DOB
= AOC + COD + DOB –––––––– (2)
From (1) and (2)
AOC + COB = AOD + DOB ––––– (3)
But AOD + DOB = 90° + 90° = 180°
Hence (3) becomes AOC +COB = 180°
Hence the adjacent angles formed when one straight line stands over another are together equal to 180°.
Proof:
Let two adjacent angles ACD and DCB be supplementary i.e., ACD + DCB = 180°. It is required to prove that A, C, B are collinear. Assume that A, C, B are not collinear. Produce AC to E such that A, C, E are collinear.
ACD + DCE = 180°__________ (2)
( A, C, E are collinear and CD stands on AE)
From (1) and (2)
ACD + DCB = ACD + DCE
DCB = DCE
But, DCB DCE
( DCE is a part of DCE)
A contradiction to our assumption that A, C, B are not collinear.
Hence the points A, C, B are collinear. i.e., AC, CB are in a straight line. Hence the theorem.
Proof:
Let AB and CD be the two straight lines which intersect each another at ‘O’. Let the line OD make the adjacent angles BOC and COA with the straight line AB.
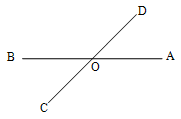
It is required to prove that
AOD + DOB + BOC + COA = 360°
We know that “the adjacent angles formed when one straight line stands over another straight line on one side of it, are together equal to 180°”.
AOD + DOB = 180° _______ (1)
and BOC + COA = 180° _______ (2)
Adding (1) and (2), we get
AOD + DOB + BOC + COA = 180° + 180° = 360°
Therefore when two straight lines intersect each other, the four angles so formed are together equal to four right angles i.e., 360°.
Proof:
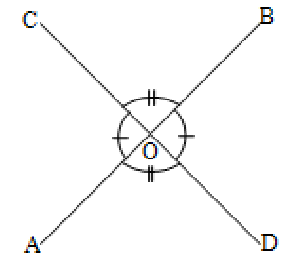
Let the straight lines AB and CD intersect each other at ‘O’.
It is required to prove that
i) AOC = BOD and ii) AOD = BOC
OA is a straight line on CD.
AOC + AOD = 180° ––––––– (1)
( linear pair of angles are supplementary) and OD meets the straight line AB.
AOD + DOB = 180° ––––––– (2)
From (1) and (2),
AOC + AOD = AOD + DOB
AOC = BOD
Again, OC meets AB,
AOC + BOC = 180° ––––––– (3)
and OA meets CD,
AOC + AOD = 180° ––––––– (4)
From (3) and (4)
AOC + BOC = AOC + AOD
AOD = BOC
Hence when two straight lines intersect each other, the vertically opposite angles are equal.
Proof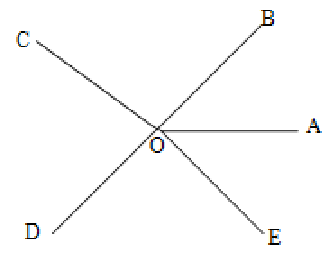
OA is a straight line, revolving about O, and turning in successively through the angles AOB, BOC, COD, DOE and EOA and returning to its original position,, will have made one complete revolutions and turned through 360°, equal to four right angles.
Therefore when a number of straight lines meet at a point, the sum of the angles so formed at that point is equal to four right angles i.e., 360°.
Properties of Angles
The adjacent angles formed when one straight line stands over another, are together equal to two right angles i.e., 180°. If two adjacent angles are supplementary, then their outer arms are in a straight line. If two straight lines intersect one another, the four angles so formed are together equal to four right angles i.e., 360°. If two straight lines intersect one another, the vertically opposite angles are equal.
When a number of straight lines meet at a point, the sum of all angles so formed at that point is equal to four right angles i.e., 360°.
5.9 Basic Theorems on Parallel Lines
Proof:
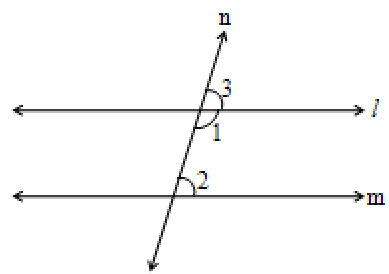
Let ‘ ’ and ‘m’ be the two coplanar lines and ‘n’ be the transversal. Then
1 + 3 = 180° ––––––– (1)
( linear pair of angles)
1 + 2 = 180° –––––––(2) (given)
Equating (1) and (2), we get 1 + 3 = 1 + 2
Cancelling ?1 on both sides, we get
3 = 2, which are corresponding angles.
According to the corresponding angles axiom, if any pair of corresponding angles are equal, then the two lines are parallel.
Hence ‘l ’ is parallel to ‘m’.
Proof:
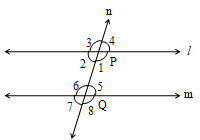
Let ‘’ and ‘m’ be the parallel lines and ‘n’ the transversal which intersects ‘ ’ and ‘m’ in such a way that 2 and 6 are one pair of interior angles on the same side of the transversal and the other such pair formed is 1 and 5.
It is required to prove that 2 + 6 = 180° and 1 + 5 = 180°.
We have 1 + 3 = 180° ––––––– (1)
( linear pair of angles)
But 3 = 6
( corresponding angles)
Substituting the value of 3 in equation (1)
we get
2 + 6 = 180° ––––––– (2)
Again 1 + 4 = 180° ––––––– (3)
( linear pair of angles)
But 4 = 5 ( corresponding angles)
Substituting the value of 4 in equation (3), we get,
1 + 5 = 180° ––––––– (4)
From (2) and (4), we get
2 + 6 = 1 + 5 = 180°
Hence proved .
Proof:
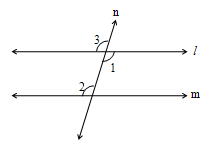
Let the two coplanar lines be ‘ ’ and ‘m’ and ‘n’ be the transversal intersecting ‘’ and ‘m’ in such a way that a pair of alternate angles are equal i.e., 1 = 2.
It is required to prove that || m.
We have 1 = 3 ––––––– (1)
( vertically opposite angles)
But given that 1= 2 ––––––– (2)
From (1) and (2), we get
2 = 3, which are corresponding angles.
According to the corresponding angles axiom, if the two lines are parallel,
Hence ‘’ is parallel to ‘m’.
Proof:
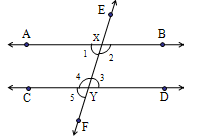
Given AB and CD are parallel lines and EF is the transversal intersecting AB and CD at ‘X’ and ‘Y’.
1, 3 are one pair of alternate interior angles and 2, 4 are another pair of alternate interior angles.
It is required to prove that 1 = 3 and 2 = 4.
We have 1 = 5
( corresponding angles) ––––––– (1) and
5 = 3
( vertically opposite angles) ––––––– (2)
From (1) and (2)
1 = 5 = 3
1 = 3
Since XY is a ray on line AB
1 + 2 = 180°
( linear pair of angles)
Also YX is a ray on line CD
3 + 4 = 180°
( linear pair of angles)
1 +2 = 3 + 4
But 1 = 3
2 = 4
Hence if a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
Proof:
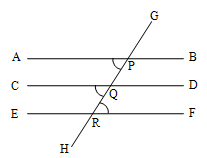
Let the straight lines AB, CD be parallel to the straight line EF. It is required to prove that AB and CD are parallel to each other.
Draw a line, GH, cutting AB, CD and EF at P,Q and R.
Since AB || EF, and GH meets them.
APR = PRF ––––––– (1) ( alternate angles)
Also CD || EF and GH meets them,
CQR = PRF ––––––– (2)( alternate angles)
From (1) and (2) APR = CQR
i.e., the corresponding angles are equal.
Hence AB and CD are parallel.
The lines which are parallel to the same straight line are parallel to one another.
Proof:
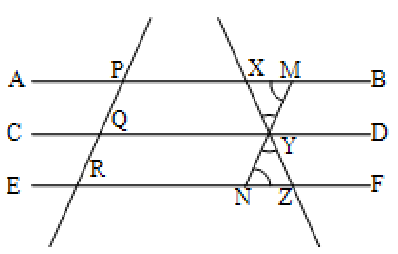
Let the parallel lines AB, CD and EF cut equal intercepts PQ and QR from the transversal PQR.
Let XY, YZ be the corresponding intercepts cut from another transversal XYZ.
It is required to prove that XY = YZ.
Through Y draw a line MN parallel to PR and touching the lines AB and EF.
Since PM || QY and PQ || MY, therefore PMY Q is a parallelogram ––––––– (1)
Similarly QYNR is also a parallelogram –––– (2)
From (1) and (2)
PQ = MY (opposite sides of a parallelogram)
and QR = YN (opposite sides of a parallelogram)
But PQ = QR MY = YN
In ’s XYM and NYZ, YM = NY
XYM = NYZ (vertically opposite angles)
XMY = YNZ (alternate interior angles)
XYM NYZ (by ASA congruent rule).
Hence XY = YZ
Note: Converse of Intercept Theorem does not exist. For example, consider the quadrilateral ABCD, where AB is not parallel to CD. Let P, Q be the midpoints of AD and BC.
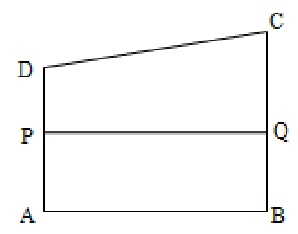
Now AP = PD and BQ = QC. But AB, PQ and DC are not parallel.
But in case AB || DC, and if P and Q are midpoints of AD and BC then AB, PQ and DC are parallels.
Properties of Parallel Lines
1. If a transversal intersects two coplanar lines in such a way that
a) A pair of alternate angles are equal, then the two lines are parallel.
b) A pair of interior angles on the same side of the transversal are supplementary, then the two lines are parallel..
2. If a transversal intersects a pair of parallel lines, then
a) The interior angles on the same side of the transversal are supplementary.
b) Each pair of alternate interior angles are equal.
3. Straight lines which are parallel to the same straight lines are parallel to one another.
4. If there are three or more parallel straight lines, and the intercepts made by them on any transversal are equal, then the corresponding intercepts made by them on any other transversal are also equal.








