4.1 Introduction
The word geometry comes from the Greek words geo, meaning the earth, and metrein, meaning to measure. Geometry appears to have originated from the need for measuring land.
This branch of mathematics was studied in various forms in every ancient civilisation, be it in Egypt, Babylonia, China, India, Greece, the Incas, etc.

The people of these civilisations faced several practical problems which required the development of geometry in various ways.
For example, whenever the river Nile overflowed, it wiped out the boundaries between the adjoining fields of different land owners.

After such flooding, these boundaries had to be redrawn.
For this purpose, the Egyptians developed a number of geometric techniques and rules for calculating simple areas and also for doing simple constructions.
The knowledge of geometry was also used by them for computing volumes of granaries, and for constructing canals and pyramids.

They also knew the correct formula to find the volume of a truncated pyramid.
You know that a pyramid is a solid figure, the base of which is a triangle, or square, or some other polygon, and its side faces are triangles converging to a point at the top.
Likewise, there are many examples that show geometry was being developed and applied everywhere in the world.
But this was happening in an unsystematic manner.
What is interesting about these developments of geometry in the ancient world is that they were passed on from one generation to the next, either orally or through palm leaf messages, or by other ways.

The geometry developed by Egyptians mainly consisted of the statements of results.
In fact, Babylonians and Egyptians used geometry mostly for practical purposes and did very little to develop it as a systematic science.
But in civilisations like Greece, the emphasis was on the reasoning behind why certain constructions work.
The Greeks were interested in establishing the truth of the statements they discovered using deductive reasoning .
A Greek mathematician, Thales is credited with giving the first known proof.
This proof was of the statement that a circle is bisected by its diameter.


4.2 Euclid’s Definitions
Euclid’s Definitions
Euclid is known as the Father of Geometry.
He is credited for organising all the works of mathematics, then known, into a logical representation in Elements, which is a collection of thirteen books.
In the Elements, Euclid begins with a list of twenty-three definitions, describing things such as points, lines, plane surfaces, circles, obtuse and acute angles, etc.
These definitions were based on the studies of the space and the objects visible in daily life.

1. Point
A point is that which has no part.
2. Line
A line is a breadth less length.
3. Points
The extremities of a line are called points.
4. Straight line
A straight line is a line which lies evenly with the points on itself.
5. Surface
A surface is that which has length and breadth only.
6. Edges
The edges of a surface are lines
7. Plane Surface
A plane surface is a surface which lies evenly with the straight lines on itself.
8. Plane Angle
A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
9. Rectilinear
When the lines containing the angle are straight, the angle is called rectilinear.
10. Perpendicular
When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
11. Obtuse Angle
An obtuse angle is an angle greater than a right angle.
12. Acute Angle
An acute angle is an angle less than a right angle.
13. Boundary Points
A boundary points out the limit or extent of something.
14. Figure
A figure is that which is contained by any boundary or boundaries.
15. Circle
A circle is a plane figure consisting of a set of points which are equidistant from a reference point.
16. Centre
This reference point is called the centre of the circle.
17. Diameter
A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
18. Semi-circle
A semi-circle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semi-circle is the same as that of the circle.
19. Rectilinear Figures
Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
20. Trilateral figures
Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle is that which has two of its sides alone equal, and a scalene triangle is that which has its three sides unequal.
21. Quadrilateral figures
A square is that which is both equilateral and right-angled, an oblong is that which is right-angled but not equilateral, a rhombus is that which is equilateral but not right-angled, and a rhomboid is that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezium.
22. Parallel lines
Parallel lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
4.3 Euclid’s Axioms
Euclid organized all the known works of mathematics at his time into Elements, a collection of thirteen books.
Each book contains a series of propositions or theorems, varying in number from about ten to hundred. These propositions or theorems are preceded by definitions.
In Book I, twenty-three definitions are followed by five postulates.
Five common notions or axioms are listed after the postulates.
He assumed certain properties that were not to be proved.
Those properties were universal truths.
Euclid divided them into Axioms and Postulates.
Some of those properties were not specific to geometry, and he called them common notions (or axioms).
1. Things which are equal to the same thing are equal to one another.
2. If equals are added to equals, the wholes are equal.
3. If equals are subtracted from equals, the remainders are equal.
4. Things which coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Things which are double of the same things are equal to one another.
7. Things which are halves of the same things are equal to one another.
Axiom 1
Suppose the area of a rectangle is equal to the area of a triangle and the area of that triangle is equal to the area of a square. By applying Euclid’s first axiom, we can say that the areas of the triangle and the square are equal. Similarly, if a = b and b = c, then we can also say that a = c.
Axiom 2
Let us consider a line segment AD in which, AB = CD.
![]()
If we add BC to both sides of this relation (equals are added), then according to Euclid’s second axiom, we can say that, AB + BC = CD + BC i.e., AC = BD.
Axiom 3
Consider the rectangles ABCD and PQRS drawn in the given figure.
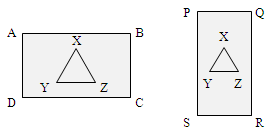
Suppose that the areas of the rectangles ABCD and PQRS are equal. If we remove triangle XYZ from each of the two rectangles as shown in the figure, then we can say that the areas of remaining portions of the two triangles are equal. We derived this from Euclid’s third axiom.
Axiom 4
Euclid’s fourth axiom is sometimes used in geometrical proofs. Let us consider a point Q that lies between points P and R of a line segment PR as shown in the figure.
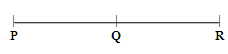
From this figure, we can notice that (PQ + QR) coincides with the line segment PR. Thus, by using Euclid’s fourth axiom, which states that “things which coincide with one another are equal to one another”, we can write, PQ + QR = PR.
Axiom 5
Using the same figure that we used in the fourth axiom, we can see that PQ is a part of line segment PR. By using Euclid’s fifth axiom, we can say that the whole i.e., line segment PR is greater than the part i.e., PQ. Mathematically, we can write it as PR > PQ.
Axiom 6 & 7
Euclid’s sixth and seventh axioms are interrelated. Let us consider two identical circles with radii and respectively.
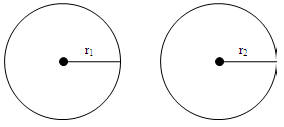
Suppose their diameters are and respectively.
As these are identical circles, their radii are equal.
=
Using Euclid’s sixth axiom, we can say 2 = 2
=
Therefore, we can say that when the radii of two circles are equal, then their diameters are also equal.
If instead of taking the radii as equal, we say that the diameters of the two circles are equal, then using the seventh axiom, we can say that the radii of the two circles are also equal.
Let us solve some examples to understand the concept better.
4.4 Euclid’s Postulates
Along with the definitions that Euclid gave in Elements, he assumed certain properties that were not to be proved.
Five of those properties were specifically geometric, and he called them postulates.
Postulate -1
It is possible to draw a straight line from any point to any other point.
Note that this postulate tells us that at least one straight line passes through two distinct points, but it does not say that there cannot be more than one such line.
However, in his work, Euclid has frequently assumed, without mentioning, that there is a unique line joining two distinct points. We state this result in the form of an axiom as follows:
Given two distinct points, there is a unique line that passes through them.
How many lines passing through P also pass through Q?
Only one, that is, the line PQ.
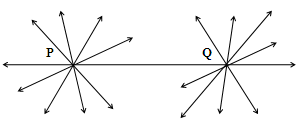
How many lines passing through Q also pass through P?
Only one, that is, the line PQ.
Thus, the statement above is self-evident, and so is taken as an axiom.
Postulate -2
A terminated line can be produced indefinitely.
Note that what we call a line segment now-a-days is what Euclid called a terminated line.
So, according to the present day terms, the second postulate says that a line segment can be extended on either side to form a line.

Postulate -3
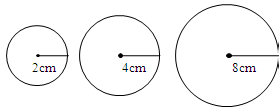
It is possible to describe a circle with any centre and radius.
According to Euclid, a circle is a plane figure consisting of a set of points that are equidistant from a reference point. It can be drawn with the knowledge of its centre and radius.
The shapes of circles do not change when different radii are considered. Only their sizes change.
Postulate -4
All right angles are equal to one another.
A right angle is unique in the sense that it measures exactly 90°. Hence, all right angles are of the measure 90° irrespective of the lengths of their arms. Hence, all right angles are equal to each other.
Remark: Unlike right angles, acute and obtuse angles are not unique in the sense that their measures lie between 0° to 89° and 91° to 179° respectively. Hence, the measure of one acute angle is not the same as the measure of another acute angle. Similarly, each obtuse angle has a different measure.
Postulate-5
Euclid stated five postulates in his work – Elements. The fifth postulate that he gave is as follows.
If a straight line falling on two straight lines forms the interior angles that together measure less than two right angles on the same side of it, then the two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles.
According to this postulate, if the sum of two angles A and B (refer figure) formed by a line l and two other lines and is less than two right angles (i.e., A + B < 180°), then lines and meet on the same side of angles A and B when extended indefinitely.
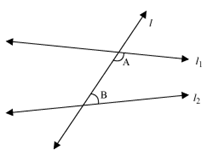
Here, A – B < 180°
Now, if we extend the lines and on the same side, then we will find that the distance between these lines goes on decreasing. It suggests that these lines will meet each other after some finite distance. This is shown in the following figure.
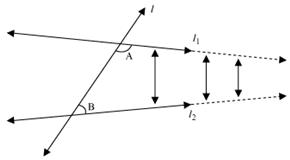
It is important to note the fact that two other cases arise for the same situation.
Case I
If the sum of angles A and B is greater than two right angles, then the two lines will never meet, no matter how long they are extended in that direction.
Case II
If the sum of angles A and B is exactly equal to two right angles, then the two lines will never meet, no matter how long they are continued in both directions.
Hence, we find that Euclid’s postulate indirectly confirms the existence of parallel lines.
Even after Euclid, mathematicians from around the world tried to prove his fifth postulate by using the other four. They provided different versions of his postulate, which indirectly show the existence of parallel lines.
One such explanation was given by John Playfair. According to Playfair’s axiom,
For every line in a plane, there exists another unique line in the same plane parallel to the given line, which passes through a point placed at a certain distance from that line.
This can be understood from the following figure.
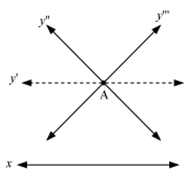
It is clear from the figure that out of the various lines passing through the point A, only line y| is parallel to line x. This is in accordance with the given statement.
Solved Examples
Example 1: If A, B and C are three points on a line, and B lies between A and C, then prove that AB + BC = AC.
![]()
Solution: In the figure given above, AC coincides with AB + BC.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that
AB + BC = AC
Note that in this solution, it has been assumed that there is a unique line passing through two points.
Example 2: Prove that an equilateral triangle can be constructed on any given line segment.
Solution: In the statement above, a line segment of any length is given, say AB.
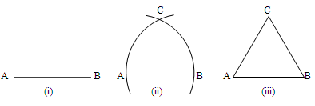
Here, you need to do some construction.
Using Euclid’s Postulate 3, you can draw a circle with point A as the centre and AB as the radius.
Similarly, draw another circle with point B as the centre and BA as the radius. The two circles meet at a point, say C. Now, draw the line segments AC and BC to form “ ABC.
So, you have to prove that this triangle is equilateral, i.e., AB = AC = BC.
Now, AB = AC, since they are the radii of the same circle ____ (1)
Similarly, AB = BC (Radii of the same circle) _____(2)
From these two facts, and Euclid’s axiom that things which are equal to the same thing are equal to one another, you can conclude that AB = BC = AC.
So, ABC is an equilateral triangle.
Note that here Euclid has assumed, without mentioning anywhere, that the two circles drawn with centres A and B will meet each other at a point.
Now we prove a theorem, which is frequently used in different results:
Example 3. Consider the following statement : There exists a pair of straight lines that are everywhere equidistant from one another. Is this statement a direct consequence of Euclid’s fifth postulate? Explain.
Solution: Take any line and a point P not on .
Then, by Playfair’s axiom, which is equivalent to the fifth postulate, we know that there is a unique line m through P which is parallel to .
Now, the distance of a point from a line is the length of the perpendicular from the point to the line.
This distance will be the same for any point on m from and any point on from m.
So, these two lines are everywhere equidistant from one another.
Remark: The geometry that you will be studying in the next few chapters is Euclidean Geometry.
However, the axioms and theorems used by us may be different from those of Euclid’s.








