Circles Book

11.1. INTRODUCTION
The collection of all the points in a plane which are at a fixed distance from a fixed point In the plane is called a circle.
11.2. TERMS RELATED TO A CIRCLE
Centre of the Circle
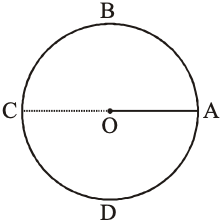
The fixed point is called the centre of the circle. O is the centre of the circle in the figure given below.
Radius of the circle
The fixed distance from the centre and circumference of the circle is called the radius of the circle. OA = OC = r is the radius of the circle. We can draw infinite radii in a circle and all are equal in length.

Chord of the circle
The line segment which joins two points on the circumference of a circle is known as the chord of the circle. The chord of a circle does not pass through the centre of the circle. CD is a chord of the circle in figure.

The diameter of the circle
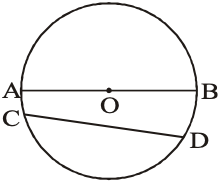
The chord, which passes through the centre of the circle, is called a diameter of the circle. We can be drawn infinite diameters in a circle and all are equal in length. In the figure, AOB is a diameter of the circle. It is denoted by d.
Now, d = 2 × r $\Rightarrow$ r = $\frac{\mathrm{d}}{2}$ [Where d = diameter and r = radius of the circle] 
N.B. Hence, it is said that a diameter is the longest chord of a circle. A circle divides the plane on which it lies into following three parts in figure.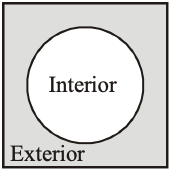

i) Interior of the circle : The plane which exists inside of a circle or the region inside of a circle is known as the interior of the circle.
ii) Circle : The geometrical figure which is surrounded by a circular line segment or a circle is a collection of all those points in a plane that are at given constant distance from a given fixed point in the plane.
iii) Exterior of the circle : The plane which exists outside of a circle or the region outside of a circle is known as the exterior of the circle.
Arc of a circle
A continuous piece of a circle is called an arc of the circle.

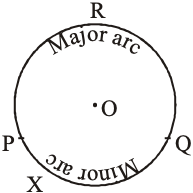
Minor arc
The shorter (smaller) arc of a circle is called minor arc. In figure, $\stackrel{⏜}{PQ}$ is the minor arc.
Major arc
The longer arc of a circle is called major arc. In figure. $\stackrel{⏜}{PRQ}$ is the major arc.
Semi circle

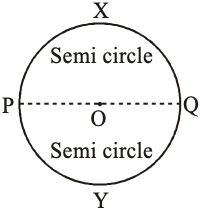
If P and Q are ends of a diameter then both arcs are equal and each is called a semi circle, i.e., $\stackrel{⏜}{PXQ}$ and $\stackrel{⏜}{PYQ}$ are equal arcs having a semi-circle in figure. It is also called semicircular region.
Circumference
The length of the complete circle is called the circumference of the circle. It is denoted by C in figure,

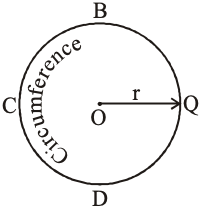
i.e. Circumference of the circle (C) = 2$\mathrm{\pi }$r; where $\mathrm{\pi }=\frac{22}{7}$ or 3.14
Semi Circumference
Half length of the complete circle is called the semi-circumference of the circle. Both semi-circumferences of the circle are equal in length in figure.

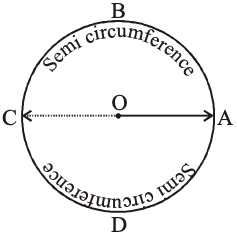
i.e. Semi circumference = $\mathrm{\pi }$.r
Segment of the circle
The region between a chord and either of its arcs is called a segment of the circle.

Minor Segment
The smaller region between a chord and smaller arc is called the minor segment of the circle, i.e. PXQ is the minor segment of the circle in figure.
Major segment
The bigger region between a chord and bigger arc is called the major segment of the circle, i.e., PYQ is the major segment of the circle in figure.
Minor sector

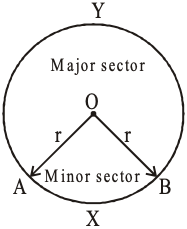
When a circle is divided by its two radii, the smaller region of the circle is called minor sector, e.g., OAXB is the minor sector of the circle in figure.  
Major Sector
When a circle is divided by its two radii, the bigger region of the circle is called major sector, e.g. OAYB is the major sector of the circle in the figure above.
Example 1
Prove that if the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.

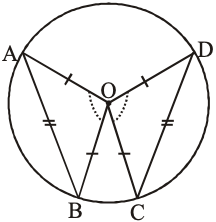
Given : In figure, chord AB = chord CD of a circle with centre O.
Construction :  joined OA, OB, OC and OD respectively.
To prove : $\angle \mathrm{AOB}=\angle \mathrm{COD}$
Proof : In ${\Delta }^{\mathrm{s}}\mathrm{AOB}\text{ and }\mathrm{COD}$, we have,
OA = OC [Radii of a circle]
OB = OD [Radii of a circle]
and AB = CD [Given]
$\therefore \Delta \mathrm{AOB}\cong \Delta \mathrm{COD}$ [By SSS congruence rule]
Hence, $\angle \mathrm{AOB}=\angle \mathrm{COD}$ [By CPCT]
Example 2
Prove that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

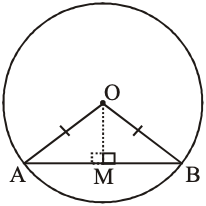
Given : OM $\perp$ chord AB. i.e. $\angle \mathrm{OMB}=\angle \mathrm{OMA}=90°$
To prove : AM = BM
Construction : Join OA and OB respectively
Proof : In ${\Delta }^{\mathrm{s}}\mathrm{OAM}\text{ and }\mathrm{OBM}$, we have
OA = OB [Radii of a circle]
$\angle \mathrm{OMA}=\angle \mathrm{OMB}=90°$ [Given]
OM = OM [common]
$\therefore \Delta \mathrm{OAM}\cong \Delta \mathrm{OBM}$
[RHS congruence rule]
Hence, AM = BM
Given : AB is a chord of a circle with centre O. M is the mid-point of chord AB
i.e., AM = BM in figure.

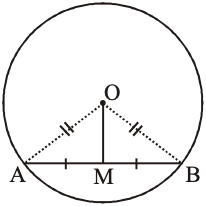
Construction : Join OM, OA and OB
To prove: OM $\perp$ AB
Proof : In ${\Delta }^{\mathrm{s}}\mathrm{OAM}\text{ and }\mathrm{OBM}$, we have
AM = BM [Given]
OA = OB [Radii of a circle]
and OM = OM  [Common]
$\therefore \Delta \mathrm{OAM}\cong \Delta \mathrm{OBM}$
[By SSS congruence rule]
$\therefore \angle \mathrm{OMA}=\angle \mathrm{OMB}$
[By CPCT] … (i)
But $\angle \mathrm{OMA}+\angle \mathrm{OMB}=180°$
[Linear pair]
$\Rightarrow \angle \mathrm{OMA}+\angle \mathrm{OMA}=180°$
[From (i)]
$\Rightarrow 2\angle \mathrm{OMA}=180°$
$\therefore \angle \mathrm{OMA}=90°$ … (ii)
$\therefore \angle \mathrm{OMA}=\angle \mathrm{OMB}=90°$
[from (i) and (ii)]
Hence, OM $\perp$ AB.
Example 3
There is one and only one circle passing through three non-collinear points.

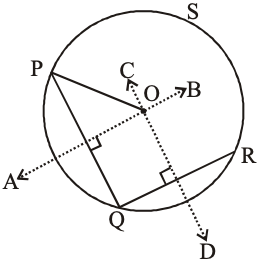
Proof : Let P, Q and R be three non-collinear points. If we join PQ and QR perpendicular bisectors of  PQ and QR intersect each other at O
Now, join OP and it is the radius of the circle, which makes the circle PQRSP and also passes through these three non-collinear points P, Q and R.
Hence, we can say that one and only one circle can be drawn through three non-collinear points.
11.3. ANGLE SUBTEND BY AN ARC
The length of the perpendicular from a point to a line is the distance of the line from the point.
Let AB be a line and P be a point. We know that there are infinite numbers of points on a line. If we join these points to P, we will get infinitely many line segments, PL₁, PL₂, PL₃, PL₄, …….. etc. in figure.

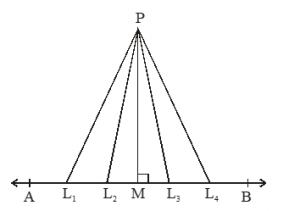
Out of these line segments, the perpendicular from P to AB i.e. PM will be the least. Hence, this least length PM has to be the distance of AB from P.
Example 3
Prove that equal chords of a circle are equidistant from the centre.

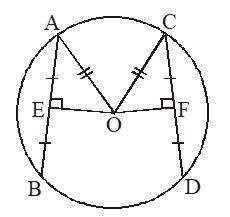
Given: AB and CD are two equal chords of a circle with centre O and OE $\perp$ AB and OF $\perp$ CD in figure.
To prove: OE = OF
Construction : Joined OA and OC
Proof : The perpendicular from the centre of a circle to a chord bisects the chord.
Now, $\because$ OE $\perp$ AB,
$\therefore \mathrm{AE}=\frac{1}{2}\mathrm{AB}$  …(i)
and $\mathrm{OF}\perp \mathrm{CD}, \therefore \mathrm{CF}=\frac{1}{2}\mathrm{CD}$  … (ii)
But AB = CD [Given]   … (iii)
$\therefore \mathrm{AE}=\mathrm{CF}$  [From (i), (ii) and (iii)]
In ${△}^s$ OAE and OCF, we have
OA = OC  [Radii of a circle]
AE = CF  [By proof]
and $\angle \mathrm{OEA}=\angle \mathrm{OFC}=90°$  [Given]
$\therefore \Delta \mathrm{OAE}\cong \Delta \mathrm{OCF}$ [By RHS congruence rule]
Hence, OE = OF  [By CPCT]
Example 4
To prove that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Given : An arc BC of a circle subtending angles BOC at the centre O and BAC at a point A on the remaining part of the circle in figure.(i), (ii) and (iii).

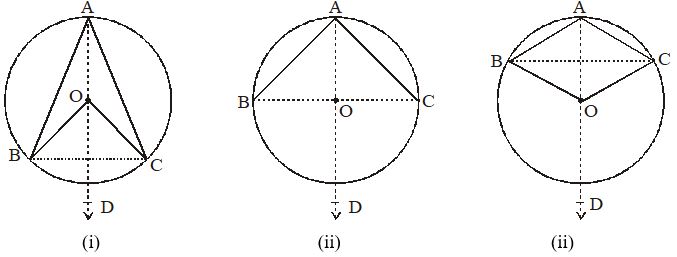
Construction : Joined AB, AC, AO and AO is extended to D.
To prove: $\angle \mathrm{BOC}=2\times \angle \mathrm{BAC}$
Proof : In different three cases, BC arc is minor in figure.(i), BC arc is semicircle in figure.(ii) and BC arc is major in figure. (iii).
Now, in all the cases: In $△$OAC, we have :
$\angle \mathrm{DOC}=\angle \mathrm{OAC}+\angle \mathrm{ACO}$ ……  (i)
[Exterior angle of a triangle is equal to the sum of two interior opposite angles]
Also, in $△$OAC, we have :
OA = OC [Radii of a circle]
$\therefore \angle \mathrm{OAC}=\angle \mathrm{ACO}$  … (ii)
[Angles opposite to equal sides of a triangle are equal]
$\therefore \angle \mathrm{DOC}=2\angle \mathrm{OAC}$  …(iii) [From (i) and (ii)]
Similarly, $\angle \mathrm{DOB}=2\angle \mathrm{OAB}$ … (iv)
Now, adding (iii) and (iv), we get
$\angle \mathrm{DOC}+\angle \mathrm{DOB}=2\angle \mathrm{OAC}+2\angle \mathrm{OAB}$
$\Rightarrow \angle \mathrm{BOC}=2\left(\angle \mathrm{OAC}+\angle \mathrm{OAB}\right)$
$\therefore \angle \mathrm{BOC}=2\angle \mathrm{BAC}$
For case (iii) in figure. (iii), where BC is the major arc, (v) is replaced by reflex angle
$\angle \mathrm{BOC}=2\angle \mathrm{BAC}$
Example 5
To prove that angles in the same segment of a circle are equal
Given : BD is an arc of a circle with centre O and $\angle \mathrm{BAD}$ and $\angle \mathrm{BCD}$ are two angles in the same segment in figure (i) and (ii).

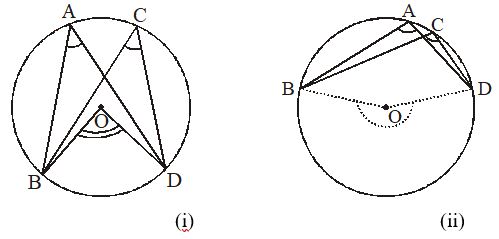
To prove : $\angle \mathrm{BAD}=\angle \mathrm{BCD}$
Construction : Joined OB and OD
Proof : We know that the angle subtended by an arc at the centre is double the angle subtended by the arc at any point in the remaining part of the circle in figure.(i)
We have $\angle \mathrm{BOD}=2\times \angle \mathrm{BAD}$  … (i)
and $\angle \mathrm{BOD}=2\times \angle \mathrm{BCD}$  .. (ii)
From (i) and (ii), we get
$\angle \mathrm{BAD}=\angle \mathrm{BCD}$
In figure (ii), we have
Reflex $\angle \mathrm{BOD}=2\times \angle \mathrm{BAD}$  …(i)
and Reflex $\angle \mathrm{BOD}=2\angle \mathrm{BCD}$  ….(ii)
From (i) and (ii), we get
$\angle \mathrm{BAD}=\angle \mathrm{BCD}$
11.4. CYCLIC QUADRILATERAL
A quadrilateral ABCD is called a cyclic quadrilateral if all the four vertices A, B, C and D are cyclic.
Example 6
AB = CB and O is the centre of the circle. Prove that BO bisects $\angle \mathrm{ABC}$

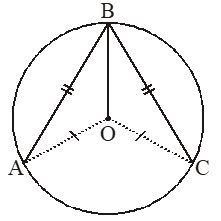
Given : In figure, AB = CB and O is the centre of the circle.
To prove : BO bisects $\angle \mathrm{ABC} i.e. \angle \mathrm{ABO}=\angle \mathrm{CBO}$
Solution : In ${\Delta }^{\mathrm{s}}\mathrm{OAB} and \mathrm{OCB}$, we have :
OA = OC [Radii of a circle]
AB = CB [Given]
and OB = OB [Common]
$\therefore \Delta \mathrm{OAB}\cong \Delta \mathrm{OCB}$ [By SSS congruence rule]
$\therefore \angle \mathrm{OBA}=\angle \mathrm{OBC}$ [By CPCT]
Hence, BO bisects $\angle \mathrm{ABC}$
Example 7
Two equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in figure. Prove that BE = DE and AE = CE in figure.

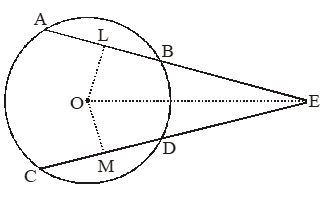
Given : AB and CD are two equal chords intersect at a point E in figure.
To prove : BE = DE and AE = CE
Construction : Joined OE OL $\perp$ AB and OM $\perp$ CD have been drawn.
Solution : $\because$ AB = CD  [Given]
$\therefore$ OL = OM [$\because$ Equal chords are equidistant from the centre]
Now, in $△S$ OLE and OME, we have
OL = OM [By proof]
$\angle \mathrm{OLE}=\angle \mathrm{OME}$  [Each equal to 90^o]
and OE = OE [Common]
$\therefore \Delta \mathrm{OLE}\cong \Delta \mathrm{OME}$  [By RHS congruence rule]
$\therefore \mathrm{LE}=\mathrm{ME}$ [$\because$ BY C.P.C.T.]
Now, AB = CD …(i)
$\Rightarrow \frac{1}{2}\mathrm{AB}=\frac{1}{2}\mathrm{CD}\Rightarrow \mathrm{BL}=\mathrm{DM}$  … (ii)
Subtracting equation (ii) from (i), we get
LE – BL = ME – DM $\Rightarrow$ BE = DE
Again, AB = CD and BE = DE
Adding both of them, we get
AB + BE = CD + DE $\Rightarrow \mathrm{AE}=\mathrm{CE}$
Hence, BE = DE and AE = CE.