Squates and Square roots

6.1. Introduction
You know that the area of a square = side × side Let us observe the following table.

What is special about the numbers 4, 9, 25, 64 and other such numbers?
Since, 4 can be expressed as 2 × 2 = $2^2$, 9 can be expressed as 3 × 3 = $3^2$, all such numbers can be expressed as the product of the number with itself.
Such numbers like 1, 4, 9, 16, 25, ….. are known as square numbers of 1, 2, 3, 4, 5,…… respectively.
6.2. Perfect square
A natural number is said to be perfect square, If it is the square of some other natural number.
Example: 81 = $9^2$, 4 = $2^2$, 36 = $6^2$, 10000 = ${100}^2$.
Identifying a perfect square:
A given number is perfect square, if it can be expressed as the product of pair of equal factors.
Note: The factors can be found by prime factorisation method.
Example1: Is 225 a perfect square ?
Resolving 225 into prime factors,

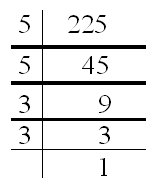
we get, 225 = × $\boxed{5\times 5}$ $\times$$\boxed{3\times 3}$
as it is expressed as the product of equal factors.
Hence, it is a perfect square.
Example2: Is 180 a perfect square ?
Resolving 180 into prime factors,
we get, 180 = $\boxed{2\times 2}$×$\boxed{3\times 3}$ × $\boxed{ 5 }$
Though 2 and 3 are paired, 5 is not paired.
Thus, 180 cannot be expressed as the product of pairs of equal factors.
Hence, 180 is not a perfect square.
Some more examples:

Note: Though 5 can be expressed as $\sqrt{5}\times \sqrt{5}$  it is not a prefect square because $\sqrt{5}$  is not a natural number.
Similarly, 21 is also not a perfect square.
6.3. Properties of squares of numbers
i) The square of an even number is always an even number.
Example:
6 is an even number and $6^2$= 36 which is even.
8 is an even number and $8^2$ = 64 which is even.
ii) The square of an odd number is always an odd number.
Example:
7 is an odd number and $7^2$ = 49 which is odd.
11 is an odd number and ${11}^2$ = 121 which is odd.
iii) The square of a proper fraction is less than the proper fraction.
6.4. Patterns of square numbers
i) Sum of first n odd natural numbers is $n^2$.
Example:
1           =  1 =  $1^2$
[one odd number]
1   +   3         = 4 = $2^2$
[sum of first two odd numbers]
1 + 3 + 5         = 9 = $3^2$
[sum of first three odd numbers]
1 + 3 + 5 + 7 […..]             = 16 = $4^2$
1 + 3 + 5 + 7 + 9 […..]          = 25 = $5^2$
1 + 3 + 5 + 7 + 9 + 11 […..]        = 36 = $6^2$
ii) Observe the squares of numbers 1, 11, 111…etc. They give a beautiful pattern:
$1^2$ = 1
${11}^2$ = 121
${111}^2$ = 12321
${1111}^2$ = 1234231
${11111}^2$ = 123454321
${111111}^2$ = 12345654321
${1111111}^2$ = 1234567654321
The square of a natural number having all digits as 1 (number of ones are £ 9) results in a palindrome.
iii) Another interesting pattern:
$7^2$ = 49
${67}^2$ = 4489
${667}^2$ = 444889
${6667}^2$ = 44448889
${66667}^2$ = 4444488889
${666667}^2$ = 444444888889
The numbers 49, 4489, 444889, . . . obtained by inserting 48 into the middle of the perceiving number are squares of integers of 7, 67, 667, 6667, . . . respectively.
The fun is in being able to find out why this happens. May be it would be interesting for you to explore and think about such questions even if the answers comes some years later.
iv) The difference of odd squares of successive numbers is equal to their sum.
Example: ${17}^2$ – ${16}^2$ = 17 + 16
${101}^2$ – ${100}^2$ = 101 + 100
${235}^2$ – ${234}^2$ = 235 + 234
In general, ${\left(n+1\right)}^2$ – ${\left(n\right)}^2$ = (n + 1) + (n) = 2n + 1
v) If 1 is added to the product of two consecutive even natural numbers, it is equal to the square of the only odd natural number between them:
2 × 4 + 1 = 9 = $3^2$
4 × 6 + 1 = 25 = $5^2$
6 × 8 + 1 = 49 = $7^2$
8 × 10 + 1 = 81 = $9^2$
10 × 12 + 1 = 121 = ${11}^2$
vi) The squares of natural numbers like 11, 111, ….., have a nice pattern as shown below
121 × (1 + 2 + 1) = 484 = ${22}^2$
${11}^2$ × (sum of the digits in ${11}^2$) = ${\left(2\times 11\right)}^2$
12321 × (1 + 2 + 3 + 2 + 1) = 110889 = ${333}^2$
${111}^2$ × (sum of the digits in ${111}^2$) = ${\left(3\times 111\right)}^2$
1234321 × (1 + 2 + 3 + 4 + 3 + 2 + 1)
= 19749136 = ${\left(4444\right)}^2$
${1111}^2$ × (sum of the digits in ${1111}^2$) = ${\left(4\times 1111\right)}^2$
$\left(square of a number having all ones\right)\times \left(Sum of digits in the square\right)$

$={\left(number of digits in the number \times the number\right)}^2$
6.5. Pythagorean triplet
Let us observe the sum of squares of 3 and 4
i.e., $3^2$ + $4^2$ = 9 + 16 = 25
$\Rightarrow$ $3^2$+ $4^2$ = $5^2$
Here, the sum of squares of 3 and 4 is square of another number 5.
$\because$ The sum of squares of two numbers is again square of another number.
$\because$ The three numbers (3, 4, 5) are said to be Pythagorean triplets.
In general, a triplet (m, n and p ) of natural numbers m, n and p is said to be a Pythagorean triplet if $m^2$ + $n^2$ = $p^2$.
Note: if m > 1 and
i) If m is odd, then the Pythagorean triplet is $\left(m,\frac{m^2–1}{2},\frac{m^2+1}{2}\right)$.
Example
If one of the numbers of a Pythagorean triplet is 3, find the triplet.
Sol. As the given number 3 is odd $\left(m,\frac{m^2–1}{2},\frac{m^2+1}{2}\right)$,
i.e., m = 3
$\because$ The Pythagorean triplet is $\left(m,\frac{m^2–1}{2},\frac{m^2+1}{2}\right)$

$\text{i.e }\left(3,\frac{3^2–1}{2},\frac{3^2+1}{2}\right)\text{ i.e }\left(3,\frac{8}{2},\frac{10}{2}\right)i.e,\left(3,4,5\right)$
Thus, the required triplet is (3, 4, 5).
Note : if m > 1 and
ii) 2m is even then the Pythagorean triplet is (2m, $m^2$ – 1, $m^2$ + 1).
Example
If one of the numbers of a Pythagorean triplet is 4, find the triplet.
Sol. As the given number 4 is even
i.e., 2m = 4   $\because$m = 4/2 = 2, m = 2
$\because$ The Pythagorean triplet is (2m, $m^2$ – 1, $m^2$ + 1)
i.e., (2(2), $2^2$ – 1 , $2^2$ + 1)
i.e., (4,3,5)
Thus, the required triplet is (3,4,5).
6.6. Square roots
Let us consider ${81}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$
As 81 is raised to the power 1/2, it is said to be the square root of 81.
Denoted as $\underset{Exponential form}{{81}^{\frac{1}{2}}}=\underset{Radical form}{\sqrt{81}}$
Thus, any number a raised to the power 1/2 is said to be the square root of the given number, denoted as $\sqrt{a}$.
6.7. Finding Square root of a Number by Prime Factorization Method
In the previous topics we have seen different methods of finding the squares of numbers given. Let us now have a look at the various methods for finding the square root of the given number.
Step-1: Write the prime factorisation of the given number.
Step-2: Pair the factors such that primes in each pair are equal.
Step-3: Choose one prime from each pair and multiply all such primes.
Step-4: The product thus obtained is the square root of the given number.
Let us understand this method through the example given below.
Example: Find the square root of 24336.
$\sqrt{24336}=\sqrt{(2\times 2)\times (2\times 2)\times (3\times 3)\times (13\times 13)}$
= 2 × 2 × 3 × 13 = 156  $\therefore \sqrt{24336}=156$
6.8. Finding Square Root by Division Method
Step-1: Place a bar over every pair of digits starting from the units digit.
Step-2: Find the largest number whose square is less than or equal to the number under the left most bar taking this number as the divisor and the number under the left-most bar as the dividend. Divide and get the remainder. Quotient in this step is same as the divisor.
Step-3: Bring down the number under the next bar to the right of the remainder. This is the new dividend.
Step-4: Double the quotient and enter it with a blank on the right for the next digit of the next possible divisor.
Step-5: Find the largest possible digit to be taken beside the divisor and also to get the new digit in the quotient.
Step-6: Bring down the number under the next bar to the right of the new remainder.
Step-7: Repeat steps 4, 5 and 6 till all the bars have been considered. The final quotient is the square root.
Let us understand this method better through the following example.
Example: Find the square root of $\overline{46}$ $\overline{78}$ $\overline{56}$.
Step-1: Placing bars over every pair of digits i.e., .
Step-2: Finding the largest number whose square is less than or equal to the left most bar.
i.e., 36 < 46 $\Rightarrow$ 6 is the required divisor. Now divide 46 by 6.

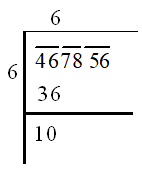
Step-3: Bring down the number under the next bar, beside the remainder of Step 2.

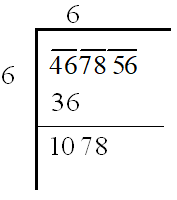
Step-4: Doubling the quotient i.e., 2 × 6 = 12.
Step-5: Guessing the largest possible digit to be taken beside the divisor and also to get the new digit in the quotient. The required digit is8. Now divide 1078 by 128 and get the remainder 54.

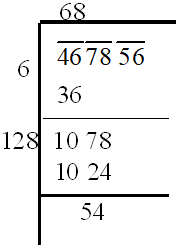
Step-6: Bringing down the number under the next bar to the right of the new remainder

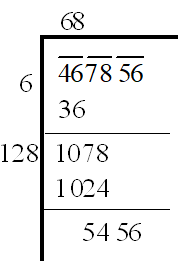
Step-7: Repeating the steps 4, 5 and 6 till all the bars have been considered. The final quotient is the required square root.

$\therefore \sqrt{467856}=684$

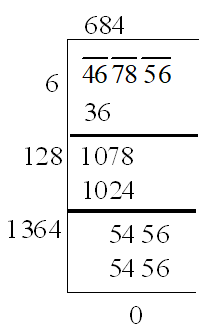
Note: This method is more efficient with larger numbers, but it can also be used to find square root of smaller numbers i.e., 3 digit or 4 digit numbers.
6.9. Finding Square Root by Assumption Method
Steps for finding the square roots up to four digit numbers, without using either factorization or division methods.
Step-1: Find the largest number whose square is less than (or) equal to the number under the left most bar. This is the tens digit of the square root.
Step-2: Find the units digit by squaring the relative number.
Step-3: Choose the correct digit by squaring one possible square root and comparing it with the given number.
Example: Find the square root of 9801.
Sol: $\overline{98} \overline{01}$
Step-1: $9^2$ = 81 is the largest square number $\le$ 98;
The tens digit in the square root of 9801 is 9.

$\therefore \sqrt{9801}=9 \boxed{?} ;$
Step-2: $1^2$ = $\boxed{1}$; $9^2$ = 8$\boxed{1}$ in both the cases, the units digit is 1.
Step-3: Trial ${91}^2$ = 8281 $\ne$9801
i.e., 1 doesn’t satisfy the units digit of square root of 9801.
$\therefore \sqrt{9801}=99$
Example: Find the square roots of 144 and 6561.
Sol: 144
Step-1: $\overline{1} \overline{44}$
$1^2$ = 1
$\therefore$Tens digit in square root of 144 is 1. $\sqrt{144}=1 \boxed{?}$
Step-2: $2^2$ = $\boxed{4}$; $8^2$ = 6 $\boxed{4}$
In both the cases, the units digit is 4.
Step-3: Trial ${12}^2$ = 144 $\therefore \sqrt{144}=12$
Example: Find the square roots of 6561.
Sol: 6561
Step-1: $\overline{65} \overline{61}$
$8^2$ = 64
$\therefore$Tens digit in square root of 6561 is 8 . $\sqrt{6561}=8 \boxed{?}$
Step-2: $1^2$ = $\boxed{1}$; $9^2$ = 8 $\boxed{1}$
In both the cases, the units digit is 1.
Step-3: Trial ${80}^2$ = 6400 is closer to 6561 than ${90}^2$ = 8100
$\therefore \sqrt{6561}$ is closer to 80 than 90
$\therefore$ The tens digit of square root may be 8
$\therefore$ square root of 6561 may be 81
Verification : 81×81=6561

$\therefore \sqrt{6561}=81$
6.10. Square roots of decimals
Step-1: Place bars on the integral part of the number in the usual manner.
Step-2: Place bars on the decimal part on every pair of digits beginning with the first decimal place.
Step-3: Start finding the square root by the division process as usual.
Step-4: Place decimal point in the quotient as soon as the integral part is over.
Step-5: Stop when the remainder is zero.
Step-6: The quotient at this stage is the square root.
Example: Find the square root of 0.00059049
Step-1: Here, integral part is 0. So place a bar on 0.
Step-2: Starting from the first decimal point, place the bars on every pair of digits. i.e., $\overline{00} \overline{05} \overline{90} \overline{49}$.
Step-3: Start finding the square root and place the decimal point in the quotient as soon as the integral part is over.

$\therefore \sqrt{0.0005905}=0.0243$
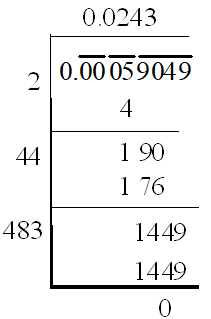
Tip (i) : If the integral part is zero in the given decimal number, then the integral part in the square root is also zero.
Tip (ii): If the first pair after the decimal point is 00, then the first digit after the decimal in the square root is also zero.
6.11. Square root of a Rational Number
For any two rational perfect squares m and n $\left(n\ne 0\right)$, $\sqrt{\frac{m}{n}}=\frac{\sqrt{m}}{\sqrt{n}}$
Example 1: Find the square root of $21\frac{2797}{3364}$.
Square root of  $21\frac{2797}{3364}=\sqrt{21\frac{2797}{3364}}=\sqrt{\frac{73441}{3364}}=\frac{\sqrt{73441}}{\sqrt{3364}}$
Let us first find $\sqrt{73441}$ by long division method:

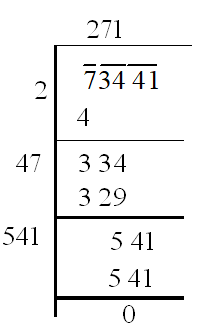
Similarly, let us find $\sqrt{3364}$.

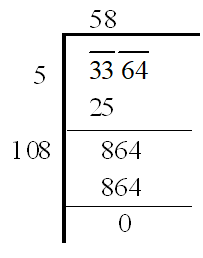
Thus, we have $\sqrt{73441}$= 271 and $\sqrt{3364}$= 58.

$\therefore \sqrt{21\frac{2797}{3364}}=\frac{271}{58}=4\frac{39}{58}.$

Example 2:

$\sqrt{\frac{25}{36}}=\sqrt{\frac{5^2}{6^2}}=\sqrt{{\left(\frac{5}{6}\right)}^2}=\frac{5}{6}\left[\because \frac{{\mathrm{a}}^2}{{ \mathrm{b}}^2}={\left(\frac{\mathrm{a}}{\mathrm{b}}\right)}^2\right]$

6.12. Square root of Integers
For any two integral perfect squares a and b (b$\ne$0),
$\sqrt{a\times b}=\sqrt{a}\times \sqrt{b}$.
Example 1: $\sqrt{25\times 36}$ = $\sqrt{5^2\times 6^2}=\sqrt{(5\times 6{)}^2}$
= 5 × 6 = 30
($\because$ for any two integers a and b,
${\left(a\times b\right)}^2$= $a^2$× $b^2$)
Example 2: $\sqrt{25}\times \sqrt{36}=\sqrt{5^2}\times \sqrt{6^2}$
= 5 × 6 = 30
From examples (1) & (2), we notice that
$\therefore \sqrt{25\times 36}=\sqrt{25}\times \sqrt{36}$
Note: 1)$\sqrt{a+b}\ne \sqrt{a}+\sqrt{b}$. 2) $\sqrt{a–b}\ne \sqrt{a}–\sqrt{b}$.
6.13. Square Roots of Imperfect Squares
Till now, we have learnt how to find square roots of numbers which are perfect squares.
Now, let us find the square roots of numbers which are not perfect squares. Remember that in such cases, we add zeros after the decimal point, or after the last figure if the original number is already in decimal form. Then carry out the answer to the desired number of places.
Example: Find the square root of 1869 to 2 decimal places.
Sol : Since we have to find the square root of 1869 to 2 decimal places, we have to add 6 zeros after the decimal to form 3 pairs.

$\sqrt{1869}=\sqrt{1869.000000}$
Let us now find the square root using long division method.

$\therefore \sqrt{1869}=43.231$ to 3 decimal places $\Rightarrow \sqrt{1869}=43.23$ to 2 decimal places.