Cubes and Cube Roots - Practically Study Material

7.1. Introduction

This is a story about one of India’s great mathematical geniuses, S. Ramanujan. Once another famous mathematician Prof. G.H. Hardy came to visit him in a taxi whose number was 1729. While talking to Ramanujan, Hardy described this number “a dull number”. Ramanujan quickly pointed out that 1729 was indeed interesting. He said,“It is the smallest number that can be expressed as a sum of two cubes in two different ways”.

1729 = 1728 + 1 = $12^{3}$ + $1^{3}$ 1729 = 1000 + 729 = $10^{3}$ + $9^{3}$

1729 has since been known as the Hardy – Ramanujan Number, even though this feature of 1729 was known more than 300 years before Ramanujan.

How did Ramanujan know this? Well, he loved numbers. All through his life, he experimented with numbers. He probably found numbers that were expressed as the sum of two squares and sum of two cubes also. There are many other interesting patterns of cubes. Let us learn about cubes, cube roots and many other interesting facts related to them.

In the previous chapter, we have learnt about squares and square roots of the numbers. In this lesson we try to understand the cubes and cube roots.

7.2. Cube of a number

If a number is multiplied by itself, we say that the number is squared. In the similar manner, if a number is multiplied by itself three times, we say that the number is cubed. In other words, the square of a number when multiplied by the number itself gives the cube of the number. If n is the number, then cube of n is n × n × n (3 factors) and it is denoted by $n^{3}$ . Thus, the exponent of the cube of a number is 3.

Number	Cube of the Number /Number Cubed
1	$1^{3}$ = 1
2	$2^{3}$ =8
3	$3^{3}$ = 27
4	$4^{3}$ = 64
5	$5^{3}$ =125
6	$6^{3}$ = 216
7	$7^{3}$ = 343
8	$8^{3}$ = 512
9	$9^{3}$ = 729

The above table gives the cubes of numbers from 1 to 9.

7.3. Perfect cube
In the above table, 1, 8, 27, …, 729 are called perfect cubes or perfect third powers of 1, 2, 3 , …, 9 respectively.
A natural number is said to be a perfect cube if it is the cube of some natural number.
If small numbers are given, we can identify whether it is a perfect cube or not. But if a larger number is given then it is difficult to do so. Hence, we need a method to check whether the number is a perfect cube or not.
Test for a Perfect Cube
Let us now have a look at the method :
We know that if a prime p divides a perfect cube, then $p^{3}$ also divides this perfect cube.
Also in the prime factorisation of a perfect cube, every prime occurs 3 times or a multiples of 3 times. Thus, to check whether a number is a perfect cube or not,
i) We first prime-factorize the given number.
ii) Then group together triplets of the same prime factors.
iii) If no factor is left out, the number is a perfect cube. Otherwise, it is not a perfect cube.
Consider the following examples.
Example 1: Is 64 a perfect cube?
Let us find 64 is a perfect cube or not.

Step-1: 64 = 2 × 2 × 2 × 2 × 2 × 2 (prime factorisation)
Step-2: 64 = (2 × 2 × 2) × (2 × 2 × 2) (grouping together triplets of same prime factors)
Step-3: Here, no prime factor is left out. So 64 is a perfect cube.
Example 2: Is 392 a perfect cube ?
392 = 2 × 2 × 2 ×7 × 7 (prime factorisation)
= (2 × 2 × 2) × 7 × 7 (grouping together triplets)
7 does not appear in a group of three.
So 392 is not a perfect cube.
7.4. Cubes of negative numbers
Let us consider the cubes of negative numbers :
(–1) × (–1) × (–1) = ${(- 1)}^{3}$ = $- 1^{3}$ = –1
(–3) × (–3) × (–3) = ${(- 3)}^{3}$ = – $3^{3}$ = –27
(–2) × (–2) × (–2) = ${(- 2)}^{3}$ = – $2^{3}$ = –8
(–5) × (–5) × (–5) = ${(- 5)}^{3}$ = – $5^{3}$ = –125
From the above examples, we can see that –1 , –27 , –8 and –125 are perfect cubes. Here, we can note an important idea about perfect squares and perfect cubes.
We know from the previous chapter that a negative number cannot be a perfect square.
But from the above examples we see that negative numbers may also be perfect cubes. That is,
(–1) = ( –1 × –1 × –1) is a perfect cube.
(–27) = ( –3 × –3 × –3) is a perfect cube.
(–8) = ( –2 × –2 × –2) is a perfect cube.
(–125) = ( –5 × –5 × –5) is a perfect cube.
If smaller numbers are given, to find the cube of that number is easier as we can multiply them thrice orally. But finding cubes of two digit and three digit numbers is difficult as it involves a lot of calculation. Let us now look at the alternative method to do so.

7.5. Pattern
Let us now understand the pattern of the units digits of the cubes of the numbers.

Units digit of the number (n)	Units digit of the cube ( $n^{3}$ )
0, 1, 4, 5, 6, 9	0, 1, 4, 5, 6, 9 respectively
2	8
3	7
7	3
8	2

Numbers with units digits 0, 1, 4, 5, 6, 9, the units digits of their cubes are again the same digits 0, 1, 4, 5, 6, 9.
Till now we have understood the idea of a cube and cube of a negative number and some other properties of cubes.

7.7. Cube root through prime factorisation method
Step-1: Express the given number as the product of primes.
Step-2: Make groups in triplets of the same prime.
Step-3: Find the product of the primes choosing one from each triplet.
Step-4: The product from Step 3 is the required cube root of the given number.
Example: Find the cube roots of 512 and 531441.

512 = (2 × 2 × 2) ×(2 × 2 × 2) ×(2 × 2 × 2)

$\sqrt[3]{512} = 2 \times 2 \times 2 = 8$

$∴ \sqrt[3]{512} = 8$

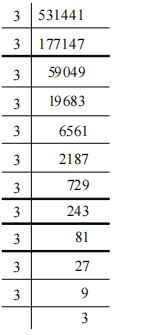
531441 = (3 × 3 × 3) × (3 × 3 × 3)× (3 × 3 × 3) × (3 × 3 × 3)

$\sqrt[3]{531441} = 3 \times 3 \times 3 \times 3 = 9 \times 9 = 81$

$∴ \sqrt[3]{531441} = 81$

Note: The cube root of the product of two perfect cubes is the product of their cube roots. For two perfect cubes x and $y, \sqrt[3]{x \times y} = \sqrt[3]{x} \times \sqrt[3]{y} .$

Example:

i) $\sqrt[3]{9261} = 21 = 3 \times 7 = \sqrt[3]{27} \times \sqrt[3]{343} = \sqrt[3]{27 \times 343}$

ii) $\sqrt[3]{91125} = 45 = 5 \times 9 = \sqrt[3]{125} \times \sqrt[3]{729} = \sqrt[3]{125 \times 729}$

iii) $\sqrt[3]{551368} = 82 = 2 \times 41 = \sqrt[3]{8} \times \sqrt[3]{68921} = \sqrt[3]{8 \times 68921}$

7.8. Cube root through Unit digit method
In this method, we can find cube root of a perfect cube by using units digit.
Let us understand the steps to be used by finding the cube root of 2197.
Step-1: Look at the digit in the units place of the perfect cube and determine the digit in the units place of the cube root.
Units digit in 2197 is 7.
Therefore, units digit in its cube root is 3.
Step-2: Strike out from the right, last three (i.e., units, tens and hundreds) digits of the number.
On striking out units, tens and hundreds digits in 2 $1$ $9$ $7$ , the left out number is 2.
Note: If nothing is left, we stop and the digit in step 1 is the cube root.
Step-3: Consider the number left out from step 2. Find the largest single digit number whose cube is less than or equal to the left out number. This is the tens digit of the cube root.
The largest single digit number whose cube is less than 2 is 1 $(∵ 1^{3} = 1 < 2)$

$∴ \sqrt[3]{2197} = 13$

Let us see one more example.
Find the cube root of 636056.
i) Units digit in 636056 is 6.
units digit in its cube root is 6.
ii) On striking out units, tens and hundreds digits in 636 $0$ $5$ $6$ , the left out number is 636.
iii) The largest single digit number whose cub e is less than 636 is 8 $(∵ 8^{3} = 512 < 636)$

$∴ \sqrt[3]{636056} = 86 .$

We have seen various methods of finding the cube roots of numbers. Let us now have a look at the method of finding cube roots of negative numbers.
7.9. Cube roots of Positive Numbers
Let us now have a look at the method of finding cube roots of positive numbers.
The cube root of the product of two perfect cubes is the product of their cube roots.
Note: For two perfect cubes x and y,

$\sqrt[3]{x \times y} = \sqrt[3]{x} \times \sqrt[3]{y}$

Examples

i) $\sqrt[3]{9261} = \sqrt[3]{27 \times 343} = \sqrt[3]{27} \times \sqrt[3]{343}$

ii) $\sqrt[3]{91125} = \sqrt[3]{125 \times 729} = \sqrt[3]{125} \times \sqrt[3]{729}$

iii) $\sqrt[3]{551368} = \sqrt[3]{8 \times 68921} = \sqrt[3]{8} \times \sqrt[3]{68921}$

7.10. Cube roots of Negative Numbers

Let us observe the following examples
Example 1: $\sqrt[3]{- 512} = \sqrt[3]{- 1 \times 512}$

$\begin{array}{l} = \sqrt[3]{- 1} \times \sqrt[3]{512} = - 1 \times 8 = - 8 \\ ∴ \sqrt[3]{- 512} = - 8 \end{array}$

Example 2 : $\sqrt[3]{- 125} = \sqrt[3]{- 1 \times 125}$

$\begin{array}{l} = \sqrt[3]{- 1} \times \sqrt[3]{125} = - 1 \times 5 = - 5 \\ ∴ \sqrt[3]{- 125} = - 5 \end{array}$

Example 3 : $\sqrt[3]{- 343} = \sqrt[3]{- 1 \times 343}$

$= \sqrt[3]{- 1} \times \sqrt[3]{343} = - 1 \times 7 = - 7$

From the above examples, we can conclude that

$\begin{array}{l} \sqrt[3]{- m} = \sqrt[3]{- 1} \times \sqrt[3]{m} = - 1 \times \sqrt[3]{m} = - \sqrt[3]{m} \\ \sqrt[3]{- m} = - \sqrt[3]{m} \end{array}$

Cube root of a negative perfect cube is negative.
Cube roots of Rational Numbers
The cube root of the quotient of two perfect cubes is the quotient of their cube roots.

For any two perfect cubes x and y, $y \neq 0, \sqrt[3]{\frac{x}{y}} = \frac{\sqrt[3]{x}}{\sqrt[3]{y}}$ is a rational number.

Example

1. Find the cube roots of $\frac{343}{125}$ .

$\sqrt[3]{\frac{343}{125}} = \frac{\sqrt[3]{343}}{\sqrt[3]{125}} = \frac{\sqrt[3]{7 \times 7 \times 7}}{\sqrt[3]{5 \times 5 \times 5}} = \frac{7}{5}$

2. Find the cube roots of $\frac{- 2197}{1331}$ .

$\sqrt[3]{\frac{- 2197}{1331}} = \frac{- \sqrt[3]{2197}}{\sqrt[3]{1331}} = \frac{- \sqrt[3]{13 \times 13 \times 13}}{\sqrt[3]{11 \times 11 \times 11}} = \frac{- 13}{11}$

Cube root of Product of Integers

Observe the following examples :

1. $\sqrt[3]{125 \times 64} =$

$\sqrt[3]{5 \times 5 \times 5 \times 4 \times 4 \times 4} = 5 \times 4 = 20_______(1)$

$\sqrt[3]{125} \times \sqrt[3]{64} = \sqrt[3]{5 \times 5 \times 5} \times \sqrt[3]{4 \times 4 \times 4}$

$= 5 \times 4 = 20_________(2)$

From (1) and (2), we have $\sqrt[3]{125 \times 64} = \sqrt[3]{125} \times \sqrt[3]{64} .$

2. $\sqrt[3]{216 \times (- 343)} = \sqrt[3]{6 \times 6 \times 6 \times (- 7) \times (- 7) \times (- 7)}$

$= 6 \times (- 7) = - 42_________(2)$

$\sqrt[3]{216} \times \sqrt[3]{(- 343)}$

$= \sqrt[3]{6 \times 6 \times 6} \times \sqrt[3]{(- 7) \times (- 7) \times (- 7)}$

$= 6 \times (- 7) = - 42____(2)$

From (1) and (2), we have

$\sqrt[3]{216 \times (- 314)} = \sqrt[3]{216} \times \sqrt[3]{(- 343)}$

From the above examples, we can conclude that for any two integers a and b, $\sqrt[3]{a \times b} = \sqrt[3]{a} \times \sqrt[3]{b} \cdot$

Need Help?