4.1. INTRODUCTION
You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle.
Since three measurements were enough to draw a triangle, a natural question arises whether four measurements would be sufficient to draw a unique four sided closed figure, namely, a quadrilateral.
4.2. CONSTRUCTION OF QUADRILATERALS WHEN ONE DIAGONAL AND FOUR SIDES ARE GIVEN
Look at the following quadrilateral ABCD.
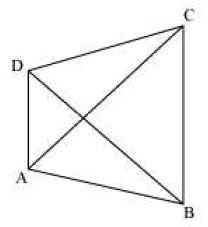
It has ten elements – four sides (AB, BC, CD, and DA), four angles (∠ABC, ∠BCD, ∠CDA, and ∠DAB), and two diagonals (AC and BD).
If we want to construct a unique quadrilateral, then how many elements are required ?
To construct a unique quadrilateral, at least five elements are necessary.
Now, suppose we want to construct a quadrilateral whose one diagonal and four sides are given, then how will we construct it ?
Steps of construction required to construct such a quadrilateral.
Let’s understand the steps from the following example . . .
Example
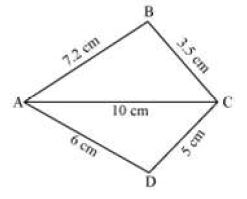
Construct a quadrilateral ABCD with AC = 10 cm, AD = 6 cm, DC = 5 cm, AB = 7.2 cm, and BC = 3.5 cm.
Solution
First, we draw a rough sketch of quadrilateral ABCD and indicate the given lengths as shown below.
The steps of construction are as follows.
i. Draw AC = 10 cm.
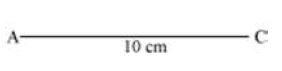
ii. Then, draw an arc taking A as centre and 7.2 cm as the radius. Now, draw another arc with C as the centre and 3.5 cm as the radius cutting the previous arc at B. Then, join AB and BC.
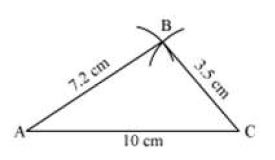
iii. Draw an arc on the opposite side of B by taking A as centre and 6 cm as the radius. Then, draw another arc with C as the centre and 5 cm as the radius cutting the previous arc at D. Then, join AD and CD.
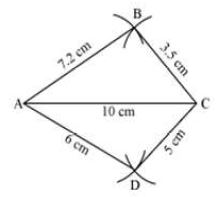
Thus, ABCD is the required quadrilateral.
Example
Can you construct a quadrilateral WXYZ with WY = 6 cm, WX = 2cm, XY = 3 cm, YZ = 6 cm, and WZ = 4.5 cm ? Justify your answer.
Solution
First, we draw a rough sketch of the quadrilateral and indicate the given lengths as shown below.
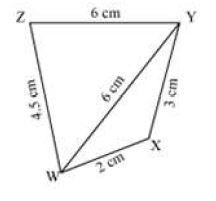
Here, in WXY,
WX + XY = 2 + 3 = 5 < WY = 6 cm
Therefore, WX + XY < WY
Sum of two sides < Third side
Therefore, WXY is not possible. Thus, we cannot construct a quadrilateral with the given lengths.
4.3. CONSTRUCTION OF A QUADRILATERAL WHEN THREE SIDES AND BOTH DIAGONALS ARE GIVEN
We know that to construct a quadrilateral, we require five elements. Now suppose three sides and the two diagonals of a quadrilateral are given.
Then, how will we construct the quadrilateral with these five elements ?
Let’s understand the steps from the following example . . .
Example
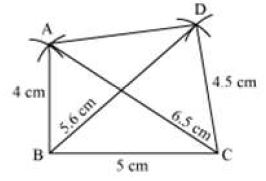
Construct a quadrilateral ABCD in which AB = 4 cm, BC = 5 cm, CD = 4.5 cm, AC = 6.5 cm, and BD = 5.6 cm.
First we draw a rough sketch of the quadrilateral ABCD and indicate the given lengths in the figure as shown below.
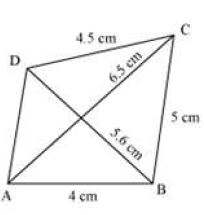
To construct the quadrilateral, we follow the below given steps.
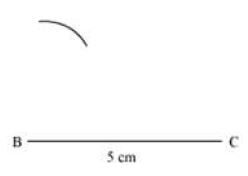
I. Draw BC = 5 cm (the side opposite to the unknown side).
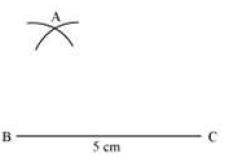
II. Then, draw an arc taking B as centre and AB (4 cm) as radius.
III. Then, draw another arc taking C as centre and AC (6.5 cm) as radius to intersect the previously drawn arc at a point A.
IV. Then, draw an arc taking B as centre and BD (5.6 cm) as radius on the same side of BC in which point A lies.
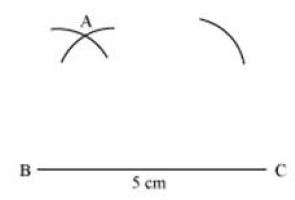
V. Then, draw another arc taking C as centre and CD (4.5 cm) as radius to intersect the arc drawn in step IV at point D.
VI. Then, join AB, AD, CD, AC, and BD.
This is the required quadrilateral ABCD.
In this way, we can construct a quadrilateral if we are given three of its sides and the two diagonals.
Let us now solve another example.
Example
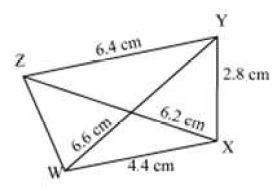
Construct a quadrilateral WXYZ in which WX = 4.4 cm, XY = 2.8 cm, YZ = 6.4 cm, XZ = 6.2 cm, and WY = 6.6 cm.
Solution
First, draw a rough sketch of quadrilateral WXYZ and indicate the given lengths as shown below.
The steps of construction are as follows.
(i) Draw XY = 2.8 cm.
(ii) Draw an arc taking X as centre and WX (4.4 cm) as radius.
(iii) Draw another arc taking Y as centre and WY (6.6 cm) as radius to intersect the previous arc at W.
(iv) Again, draw an arc taking X as centre and XZ (6.2 cm) as radius on the same side of XY in which point W lies.
(v) Draw another arc taking Y as centre and YZ (6.4 cm) as radius to intersect the arc drawn in previous step at Z.
(vi) Join XW, WZ, YZ, XZ, and WY.
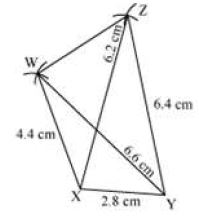
Thus, WXYZ is the required quadrilateral.
4.4. CONSTRUCTION OF QUADRILATERALS WHEN TWO ADJACENT SIDES AND THREE ANGLES ARE GIVEN
Suppose we have to construct a quadrilateral ABCD and the following elements of the quadrilateral are given.
AB = 5.5 cm, BC = 4.9 cm, “B = 120°, “C = 90°, “A = 75°.
How will we construct the quadrilateral with this information ?
Let us see.
Firstly, let us draw a rough sketch of the quadrilateral so that the process of construction becomes easier for us.
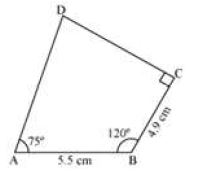
The steps of construction are as follows.
I. Firstly, we draw the line AB = 5.5 cm.
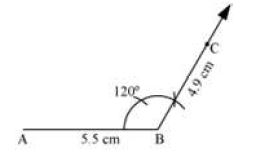
II. Then we construct an angle of 120° at B and locate the point C which is 4.9 cm away from B.
III. Now, we construct an angle of 90° at C.
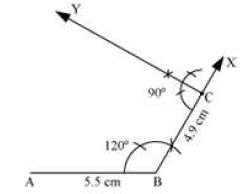
IV. Now, we construct an angle of 75° at A. CY and AZ meet at the point D.
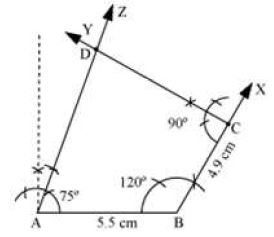
Hence, ABCD is the required quadrilateral.
In this way, we can construct a quadrilateral if two adjacent sides and three angles are given.
Let us now look at some more examples to understand this concept better.
Example
Construct a quadrilateral WXYZ with ZY = 5.9 cm, WZ = 4.5 cm, ∠Y = 90°, ∠ Z = 120°, and ∠W = 60°.
Solution
Firstly, we draw a rough sketch of the quadrilateral WXYZ and indicate the given lengths as shown in the following figure.
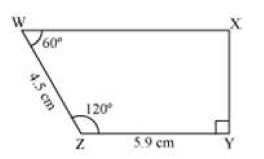
The steps of construction are as follows.
I. Firstly, we draw a line segment ZY = 5.9 cm.

II. Then we construct an angle of 120° at Z. Mark the point W, such that WZ = 4.5 cm.
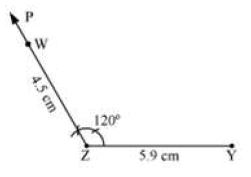
III. Now, we construct an angle of 60° at W and an angle of 90° at Y to meet the two line segments at X.
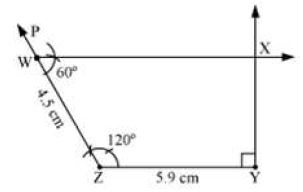
Thus, WXYZ is the required quadrilateral.
Example
Can you construct a quadrilateral ABCD with AB = 5.5 cm, BC = 4.9 cm, ∠A = 130°, ∠B = 145°, and ∠C = 95° ?
Solution
We know that the sum of all the angles of a quadrilateral is 360°.
Here, we are given that ∠A = 130°, ∠B = 145°, and ∠C = 95°.
∠A + ∠B + ∠C = 130° + 145° + 95° = 370°
This is not possible.
Thus, we cannot construct a quadrilateral with the given measurements.
4.5. CONSTRUCTION OF QUADRILATERALS WHEN THREE SIDES AND TWO INCLUDED ANGLES ARE GIVEN
We know that to construct a quadrilateral, we require five elements.
Suppose three sides and two angles included between them are given.
Then how will we construct the quadrilateral ?
Let’s see an example to understand the steps . . .
Example
Construct a quadrilateral PQRS with SR = 4.5 cm, QR = 3.9 cm, PQ = 5 cm, ∠R = 90°, and ∠Q = 120°.
Solution
Firstly, we draw a rough sketch of the quadrilateral PQRS as shown in the following figure.
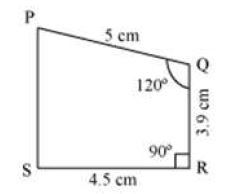
The steps of construction are as follows.
I. We draw a line segment SR of length 4.5 cm.

II. Then we construct an angle of 90° at R and locate the point Q such that RQ = 3.9 cm.
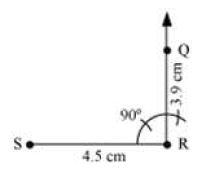
III. Now, we construct an angle of 120° at Q and locate the point P such that QP = 5 cm. Then we join PS.
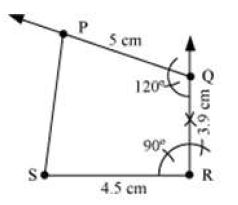
Thus, PQRS is the required quadrilateral of given measures.
4.6. CONSTRUCTION OF SOME SPECIAL QUADRILATRALS
Some special quadrilaterals such as square, rhombus, rectangle, kite, and parallelogram can be constructed by using their properties.
In a square, all the sides are equal and all the angles are equal to 90 ?. Therefore, a square can be constructed, if one of its sides is given.
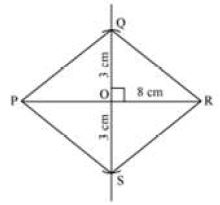
In a rhombus, all the sides are equal. Also, the diagonals of a rhombus are perpendicular bisectors of one another. Therefore, a rhombus can be constructed, if only the measures of two diagonals are given.
For example, if the diagonals of a rhombus PQRS are given as PR = 8 cm and QS = 6 cm, then draw one of the diagonals, say PR = 8 cm Then, construct its perpendicular bisector and let them meet at O.
With O as centre, cut off two arcs at the bisector on the opposite side of PR, each arc of radius 3 cm.
Then, the points, Q and S, are obtained. Join PQ, QR, PS, and SR to obtain the required rhombus, PQRS.
In a rectangle, all angles are of measure 90° and the opposite sides are equal.
Therefore, a rectangle can be constructed even if two of its adjacent sides are given.
In a kite, the adjacent sides are equal. Therefore, if two adjacent sides and a diagonal are given, then the required kite can be constructed.
In a parallelogram, the opposite sides are equal and parallel. Therefore, a parallelogram can be constructed even if two of its sides and one angle or a diagonal are given.
Example
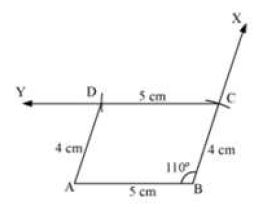
A parallelogram ABCD with AB = 5 cm, BC = 4 cm, ∠B = 110° can be constructed as follows.
First, draw AB = 5 cm and then construct ∠ABX = 110°
With B as centre, draw an arc of radius 4 cm cutting the ray, BX, to obtain the point, C. Then, draw a line CY parallel to AB. With C as centre, cut an arc of radius 5 cm at CY to obtain the point, D. Join AD to obtain the parallelogram, ABCD.