Understanding Quadrilaterals

3.1. Introduction
You know that the paper is a model for a plane surface. When you join a number of points without lifting a pencil from the paper (and without retracing any portion of the drawing other than single points), you get a plane curve.

3.2. Polygons
A simple closed curve made up of only line segments is called a polygon.

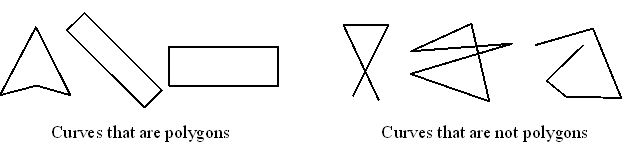
Try to give a few more examples and non-examples for a polygon.

Draw a rough figure of a polygon and identify its sides and vertices.

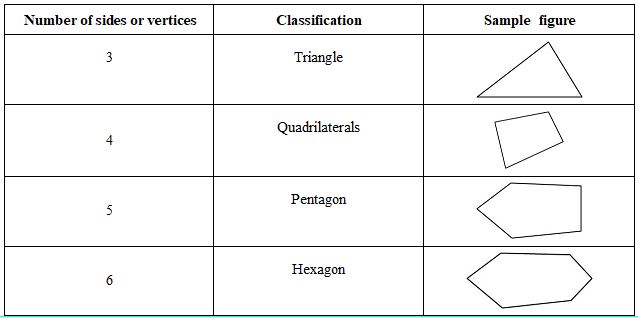
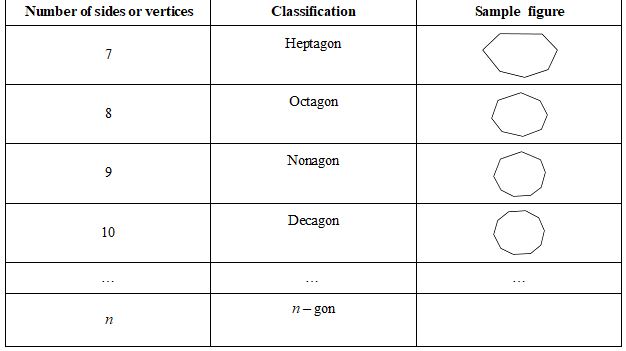
I. Classification of polygons

We classify polygons according to the number of sides (or vertices) they have.

II. Diagonals
A diagonal is a line segment connecting two non-consecutive vertices of a polygon.

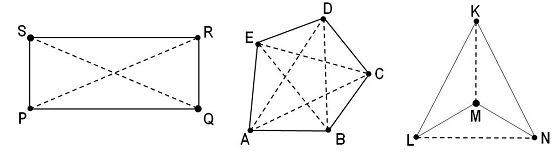
In figures given below, the shaded region shows the interior and exterior of a closed curve. The interior has a boundary and the exterior has no boundary at all

The interior has a boundary. Does the exterior have a boundary?
III. Convex and concave polygons
Here are some convex polygons and some concave polygons.

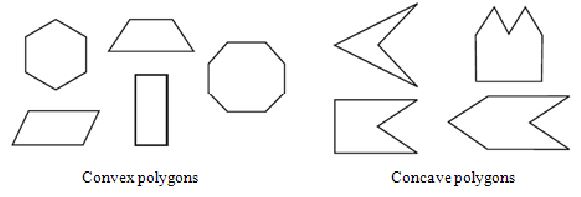
Polygons that are convex have no portions of their diagonals in their exteriors.
Polygons that may have portions of their diagonals in their exteriors are called concave polygons.
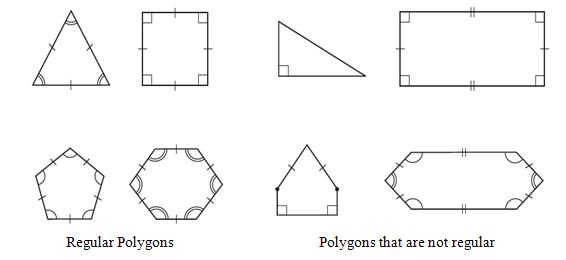
IV. Regular and irregular polygons
A regular polygon is both ‘equiangular’ and ‘equilateral’. For example, a square has sides of equal length and angles of equal measure. Hence it is a regular polygon. A rectangle is equiangular but not equilateral. Is a rectangle a regular polygon? Is an equilateral triangle a regular polygon? Why?

[Note: Use of 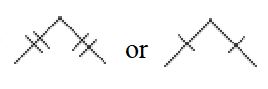 indicates segments of equal length].

Examples:
Pentagon ( 5 sides) , Hexagon ( 6 sides), heptagon (7 sides), etc.
V. Angle sum property
The sum of the measures of the three angles of a triangle is 180°.

3.3. Sum of the Measures of the Exterior Angles of a Polygon
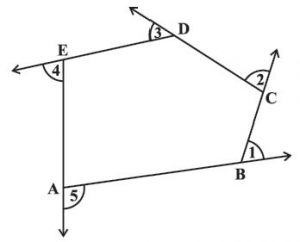
Draw a polygon on the floor, using a piece of chalk. (In the figure, a pentagon ABCDE is shown). We want to know the total measure of angles, i.e., m $\angle$1 + m$\angle$2 + m$\angle$3 + m$\angle$4 + m$\angle$5. Start at A. Walk along $\overline{AB}$ . On reaching B, you need to turn through an angle of m$\angle$1, to walk along $\overline{BC}$. When you reach at C, you ned to turn through an angle of m$\angle$2 to walk along $\overline{CD}$. You continue to move in this manner, until you return to side AB. You would have in fact made one complete turn. Therefore, m$\angle$1 + m$\angle$2 + m$\angle$3 + m$\angle$4 + m$\angle$5 = 360°. This is true whatever be the number of sides of the polygon. Therefore, the sum of the measure of the external angles of any polygon is 360°.

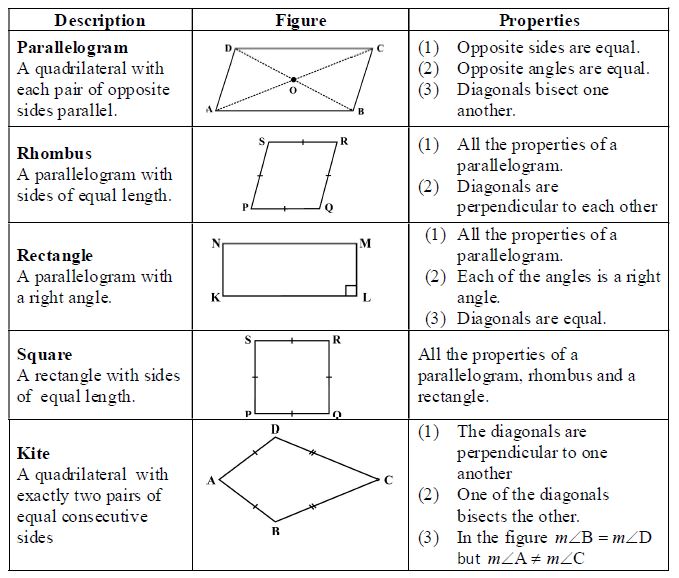
3.4. Kinds of Quadrilaterals
Based on the nature of the sides or angles of a quadrilateral, it gets special names.
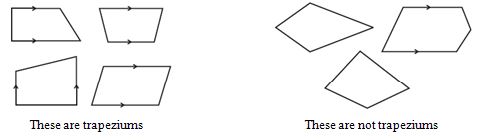
I. Trapezium
Trapezium is a quadrilateral with a pair of parallel sides.

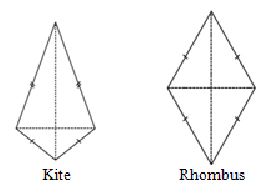
II. Kite
Kite is a special type of a quadrilateral. The sides with the same markings in each figure are equal. For example AB = AD and BC = CD.

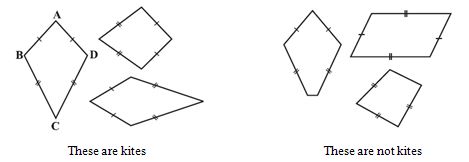
(i) A kite has 4 sides (It is a quadrilateral).
(ii) There are exactly two distinct consecutive pairs of sides of equal length.
III. Parallelogram
A parallelogram is a quadrilateral. As the name suggests, it has something to do with parallel lines.

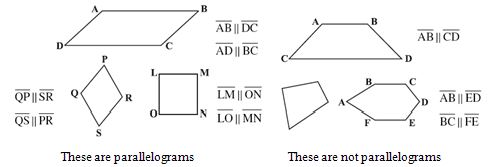
A parallelogram is a quadrilateral whose opposite sides are parallel.
IV. Elements of a parallelogram
There are four sides and four angles in a parallelogram. Some of these are equal. There are some terms associated with these elements that you need to remember.

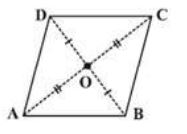
Given a parallelogram ABCD.
$\overline{AB}$ and $\overline{DC}$, are opposite sides. $\overline{AD}$ and $\overline{BC}$ form another pair of opposite sides.
$\angle A$ and $\angle C$ are a pair of opposite angles; another pair of opposite angles would be $\angle B$ and $\angle D$.
$\overline{AB}$ and  $\overline{BC}$ are adjacent sides. This means, one of the sides starts where the other ends. Are $\overline{BC}$ and $\overline{CD}$adjacent sides too? Try to find two more pairs of adjacent sides.
$\angle A$ and $\angle B$ are adjacent angles. They are at the ends of the same side. $\angle B$ and $\angle C$are also adjacent. Identify other pairs of adjacent angles of the parallelogram.
Property: The opposite sides of a parallelogram are of equal length.
You can further strengthen this idea through a logical argument also.
Consider a parallelogram ABCD (as shown in the figure).

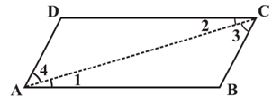
Draw any one diagonal, say $\overline{AC}$.

Looking at the angles, $\angle 1$ = $\angle 2$ and $\angle 3$ = $\angle 4$ (why?)

Since in triangles ABC and ADC, $\angle 1=\angle 2,\angle 3=\angle 4$

and $\overline{AC}$ is common, so, by ASA congruency condition,

$\Delta \mathrm{ABC}\cong \Delta \mathrm{CDA}$             (How is ASA used here?)

This gives AB = DC and BC = AD.

V. Angles of a parallelogram

Property: The opposite angles of a parallelogram are of equal measure.

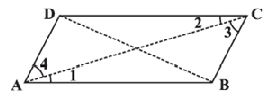
You can further justify this idea through logical arguments.

If $\overline{\mathrm{AC}}\text{ and }\overline{\mathrm{BD}}$ re the diagonals of the parallelogram, you find that

$\angle 1=\angle 2\text{ and }\angle 3=\angle 4$  (why?)

Studying separately, $\Delta \mathrm{ABC}\text{ and }\Delta \mathrm{ADC}$ will help you to see that by ASA congruency condition,

$\Delta \mathrm{ABC}\cong \Delta \mathrm{CDA}$ (HOW?)

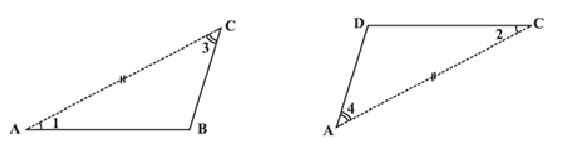
This shows that $\angle B$ and $\angle D$ have same measure. In the same way you can get $\mathrm{m}\angle \mathrm{A}=\mathrm{m}\angle \mathrm{C}$

VI. Diagonals of a parallelogram
The diagonals of a parallelogram, in general, are not of equal length. However, the diagonals of a parallelogram have an interesting property.

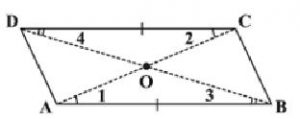
Property: The diagonals of a parallelogram bisect each other (at the point of their intersection, of course!)
To argue and justify this property is not very difficult. From Fig, applying ASA criterion, it is easy to see that $\Delta \mathrm{AOC}\cong \Delta \mathrm{COD}$ (How is ASA used here?)

This gives AO = CO and BO = DO

3.5. Some Special Parallelograms
I. Rhombus
We obtain a Rhombus (which, you will see, is a parallelogram) as a special case of kite (which is not a a parallelogram).
The sides of rhombus are all of same length; this is not the case with the kite.
A rhombus is a quadrilateral with sides of equal length.

Since the opposite sides of a rhombus have the same length, it is also a parallelogram. So, a rhombus has all the properties of a parallelogram and also that of a kite.
The most useful property of a rhombus is that of its diagonals.

Property: The diagonals of a rhombus are perpendicular bisectors of one another

Here is an outline justifying this property using logical steps.
ABCD is a rhombus (Fig).
Therefore it is a parallelogram too.
Since diagonals bisect each other, OA = OC and OB = OD.
We have to show that $m\angle \mathrm{AOD}=m\angle \mathrm{COD}=90°$

It can be seen that by SAS congruency criterion

$\Delta \mathrm{AOD}\cong \Delta \mathrm{COD}$

Therefore, $m\angle \mathrm{AOD}=m\angle \mathrm{COD}\left[\begin{array}{ll}\text{ Since }& \mathrm{AO}=\mathrm{CO} (Why\hspace{0.17em}?)\\ & \mathrm{AD}=\mathrm{CD} (Why ?)\\ & \mathrm{OD}=\mathrm{OD}\end{array}\right.$

Since $\angle AOD$ and $\angle COD$are a linear pair,
$m\angle \mathrm{AOD}=m\angle \mathrm{COD}=90°$
Example: RICE is a rhombus (Fig). Find x, y, z. Justify your findings.

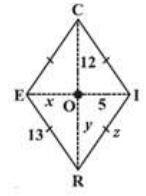
Solution:    x = OE
                    y = OR
                    z = side of the rhombus
                           = OI (diagonals bisect) = OC (diagonals bisect) = 13 (all sides are equal )
                           = 5 = 12

II. Rectangle
A rectangle is a parallelogram with equal angles (Fig ).

If the rectangle is to be equiangular, what could be the measure of each angle?
Let the measure of each angle be x°.
Then 4x° = 360°
Therefore, x° = 90°
Thus each angle of a rectangle is a right angle.
So, a rectangle is a parallelogram in which every angle is a right angle.
Being a parallelogram, the rectangle has opposite sides of equal length and its diagonals bisect each other.
In a parallelogram, the diagonals can be of different lengths. (Check this); but surprisingly the rectangle (being a special case) has diagonals of equal length.
Property : The diagonals of a rectangle are of equal length.

This is easy to justify. If ABCD is a rectangle (Fig ), then looking at triangles
ABC and ABD separately [(Fig) and (Fig ) respectively], we have

$\Delta \mathrm{ABC}\cong \Delta \mathrm{ABD}$

This is because AB = AB            (Common)

BC = AD

$m\angle \mathrm{A}=m\angle \mathrm{B}=90°$

The congruency follows by SAS criterion.
Thus AC = BD
and in a rectangle the diagonals, besides being equal in length bisect each other

6. Square
A square is a rectangle with equal sides.

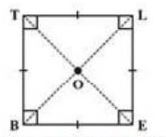
BELT is a square, BE=EL=LT=TB $\angle \mathrm{B},\angle \mathrm{E},\angle \mathrm{L},\angle \mathrm{T}$ are right angles.
BL = ET and $\overline{\mathrm{BL}}\perp \overline{\mathrm{ET}}$
OB = OL and OE = OT.

This means a square has all the properties of a rectangle with an additional requirement that all the sides have equal length.
The square, like the rectangle, has diagonals of equal length.
In a rectangle, there is no requirement for the diagonals to be perpendicular to one another.
In a square the diagonals.
(i) bisect one another                          (square being a parallelogram)
(ii) are of equal length                         (square being a rectangle) and

(iii) are perpendicular to one another.
Hence, we get the following property.
Property: The diagonals of a square are perpendicular bisectors of each other.

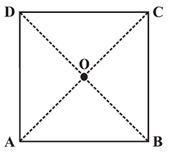
We can justify this also by arguing logically:
ABCD is a square whose diagonals meet at O (Fig).
OA = OC (Since the square is a parallelogram)
By SSS congruency condition, we now see that

$\Delta \mathrm{AOD}\cong \Delta \mathrm{COD}$

Therefore, $m\angle \mathrm{AOD}=m\angle \mathrm{COD}$

These angles being a linear pair, each is right angle.