Perimeter and Area

1. BASIC DEFINITIONS
Closed figure
A figure with no open ends is a closed figure.
Regular closed figures: A closed figure in which all the sides and angles equal.
Perimeter
Perimeter is the distance covered along the boundary forming a closed figure when we go round the figure once. The concept of perimeter is widely used in real life.
Eg: 1) For fencing land.
        2) For building a compound wall around a house.
Area
The amount of surface enclosed by a plane figure is called its area.
Mensuration
The subject of finding areas and volumes of geometrical figures is called mensuration
2. AREA AND PERIMETER OF PLANE FIGURES
Rectangle
The quadrilateral which is having pair of equal and parallel opposite sides and one angle is 90°.

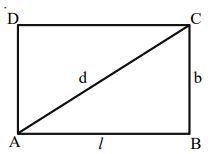
Let ABCD be a rectangle of length = l units, breadth = b units, diagonal = d units.
• Perimeter of rectangle = 2(l + b) units
• Diagonal of the rectangle, $\mathrm{d}=\sqrt{l^2+{\mathrm{b}}^2}$ units
• Area of rectangle = (l × b) sq.units
• Length $=\left(\frac{\text{ Area }}{\text{ Breadth }}\right)$ units
• Breadth $=\left(\frac{\text{ Area }}{\text{ Length }}\right)$ units

Square
The rectangle which is having all sides equal, all angles are right angles is called Square.

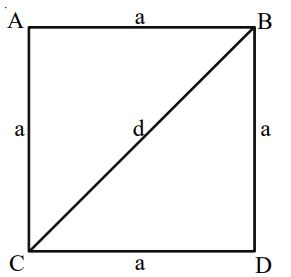
Let the side length of a square be ‘a’ units, then
• Perimeter of the square = 4a units
• Diagonal of the square $=\sqrt{a^2+a^2}=\sqrt{2a^2}=a\sqrt{2}\text{ units }$

• Area of the square = $a^2$ sq.units
• Area of the square = $\frac{1}{2}(\text{ diagonal }{)}^2\text{ Sq.units }$

• Side of the square = $\sqrt{Area}$ units

Rhombus
A parallelogram in which the all sides are equal is called a rhombus.

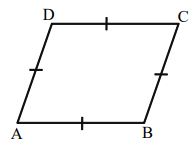
Area (A) = $\frac{1}{2}\times$Product of its diagonals 

$=\frac{1}{2}\times {\mathrm{d}}_1\times {\mathrm{d}}_2$
let side be ‘a’ then perimeter = a + a + a + a = 4a

Parallelogram
A quadrilateral in which both the pairs of opposite sides are parallel is called a parallelogram.
The perimeter of a parallelogram is twice the sum of the lengths of the adjacent sides.
In the below figure, the perimeter of parallelogram ABCD = 2(AB + BC)
The area of a parallelogram is the product of its base and perpendicular height or altitude.
Any side of a parallelogram can be taken as the base. The perpendicular dropped on that side from the opposite vertex is known as the height (altitude).
In the below figure, the area of parallelogram ABCD = AB × DE or AD × BF

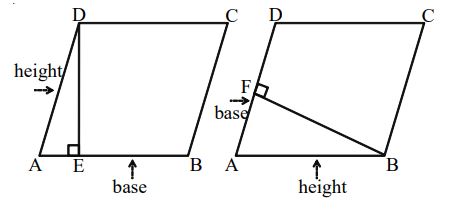
Area (A) = base height = bh

$\mathrm{b}=\frac{\mathrm{A}}{\mathrm{h}},\mathrm{h}=\frac{\mathrm{A}}{\mathrm{b}}$

let length of one side be ‘a’ and length of other side be ‘b’
Perimeter = a + b + a + b = = 2a + 2b = 2(a + b)

Trapezium
A trapezium is a shape with four sides. that has one set of parallel sides.

$\mathrm{Area}\left(\mathrm{A}\right)=\frac{1}{2}\left(\text{ Sum of parallel sides }\right)\text{ Height }=\frac{1}{2}(\mathrm{a}+\mathrm{b})\mathrm{h}$

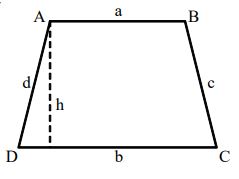
a,b = sides, h = height
Perimeter of trapezium = a + b + c + d
where a, b, c, d are sides.
Four walls of a Room
Let there a room with length = ‘$l$’ units, breadth = ‘b’ units, and height = ‘h’ units, then,
• Area of four walls = 2($l$ + b) × h Sq.units
• Diagonal of room = $\sqrt{l^2+b^2+h^2}$ units

Rectangular Path
If a rectangular path of uniform width surrounds a rectangle, then the length and the breadth of the outer rectangle are obtained by adding twice the width of the path to the length and the breadth of the inner rectangle.
Area of outer rectangle: ($l$ + 2w)(b + 2w)
Area of the path = ($l$ + 2w)(b + 2w) – $l$b
Triangle
The closed figure obtained by joining three non collinear points is called a triangle.
Let a, b, c lengths of sides triangle then s = a + b + c is a perimeter of triangle,
Area (A) $=\sqrt{s(s-a)(s-b)(s-c)}$

$s=\frac{a+b+c}{2}$is called semi perimeters of the triangle
Equilateral Triangle
A triangle which is having equal sides is called an equilateral triangle

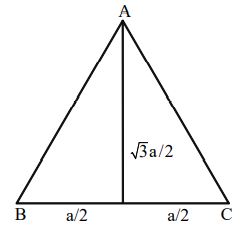
Let the side of an equilateral triangle be ‘a’ then height of equilateral triangle = $\frac{\sqrt{3}}{2}a$
Perimeter of equilateral triangle = 3a units.

$\text{ Area }=\frac{1}{2}\text{ base }\times \text{ height }\frac{1}{2}=\frac{1}{2}\mathrm{a}\cdot \frac{\sqrt{3}}{2}\mathrm{a}=\frac{\sqrt{3}}{4}{\mathrm{a}}^2$

Right Angle Triangle
In a triangle ABC if one angle is ${90}^0$, then it is called a right angled triangle

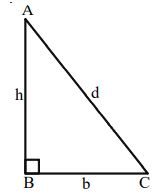
Note: If ABC is a Right Angled Triangle then by Pythagoras Theorem
$(\text{ Hypotenuse }{)}^2=(\text{ Side }{)}^2+(\text{ Side }{)}^2$
Perimeter of right angled triangle = b + h + d

$\text{ Area }\mathrm{A}=\frac{1}{2}\text{ base }\times \text{ height }=\frac{1}{2}\mathrm{bh}=\mathrm{b}\sqrt{{\mathrm{d}}^2-{\mathrm{b}}^2}$

3. MENSURATION OF CIRCLE
A circle is a closed curve in plane drawn in such a way that every point on this curve is at a constant distance(or units) from a fixed point ‘O’ inside it. The fixed point ‘O’ is called the centre of the circle and the constant distance ‘r’ is called the length of radius of the circle.
Circumference
The perimeter of a circle is called its circumference. The length of the thread that winds tightly around the circle exactly once gives the circumference of the circle.
Circumference $=2\pi \mathrm{r}=\pi \mathrm{d}$
where r = radius and d = diameter
Here $\mathrm{\pi }$(pi) is a constant.
Note: The approximate value of ‘ $\mathrm{\pi }$ ’ is taken as $\frac{22}{7}$(or)3.14.

However ‘ $\mathrm{\pi }$’ is not rational and is defined as the ratio of circumference of a circle to its diameter.

Area of a Circle
Area of a circle with radius ‘r’ units is equal to ${\mathrm{\pi r}}^2$ sq.units
Area of a Sector
A sector off a circle is the region enclosed by an arc of a circle and two radii to its end points. Where ‘x’ is sector angle. ‘r’ is the radius.
Sector area (A) = $\frac{\theta }{{360}^{\circ }}\times \text{ Area of a circle }$

4. VOLUME AND SURFACE AREA OF CUBOID AND CUBE
Volume and Surface area of Cuboid
A solid bounded by six rectangular plane faces is called cuboid.

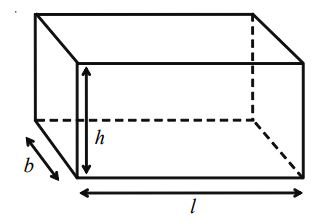
Let the Dimensions of cuboid be length = ‘l’ units, breath = ‘b’ units, height = ‘h’units, then
• Diagonal of cuboid $=\sqrt{l^2+b^2+h^2}$ units
• Total surface Area of cuboid = 2( $l$b + bh + $l$h) sq units
• Lateral surface Area of cuboid = 2 ($l$ × b)× h sq. units
• Volume of cuboid = $l$bh cubic units
• Area of 4 walls of room = 2 ($l$ × b)× h sq.units

Volume and Surface area of Cube
The cuboid whose length breath and height are equal is called a cube.

Let the edge of a cube be ‘a’ units then
• Diagonal of cube = $\sqrt{3}$ a units
• Total surface Area of cube = $6a^2$ square units
• Lateral surface Area of cube = $4a^2$ square units
• Volume of cube = $a^3$ cubic units.