Algebraic Expressions - Practically Study Material

1. INTRODUCTION
This is where your work really begins to look and feel like algebra. You are about to begin working with letters of the alphabet as well as numbers and signs of operation. From now on, letters such as x, y and z are just as common as numbers 1, 2 and 3.
So what do letters in algebra mean? Until now–-in basic arithmetic–-you work with numbers, each
number having a specific value or meaning. A “2” is a 2, for example. A “2” is always a 2–-it is never a 6 and it is never a 10. It’s like that for all numbers. We still use regular arithmetic numbers in algebra, but we also use terms expressed in letters. In algebra, the letter x, for example, can stand for a lot of different values. We can set x equal to 2 in one problem, but then set it equal to 6 in another. The letters in algebra can stand for an endless variety of values and combinations of values. Letters in algebra can even represent other letters.
Compare these two expressions
· Arithmetic expression: 2 + 1
· Algebraic expression: x + 1
The arithmetic expressions tells us to add 1 to the value of 2. The algebraic expression, however, covers a lot more territory by telling us to add a 1 to any value we choose. So if we let x = 2 in the algebraic expression, it becomes 2 + 1. If we let x = 5, it becomes the same as 5 + 1. You can see that the algebraic version is a lot more flexible than the version.
2. UNDERSTANDING AN EXPRESSION
i) A specific numerical value ( such as 2, 4, –6, ¾ ) is called a constant. The value is constant … unchanging.
ii) An algebraic term (such as x, y, a, b, and so on) is called a variable. The value can be varied.

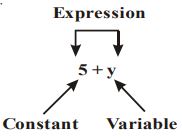
iii) When constants or variables are connected by operations (such as +, –, x , or ÷ ), you have an expression.
Forming an expression
We combine constants and variables to make algebraic expressions for this we use four basic operations of mathematics such as addition, subtraction, multiplication and division. The expression 5x + 4 is obtained from the variable x, first by multiplying x by the constant 5 and then adding constant 4 to the product.
Let’s see how the following expressions are formed.
$4 x^{2} - 5 x, 7 x y + 5, x^{2} y$
In $4 x^{2} - 5 x$ , we first obtain $x^{2}$ by multiplying the variable x by itself and then multiply $x^{2}$ by 4 to get $4 x^{2}$ .
From $4 x^{2}$ we subtract the product of 5 and x to finally arrive at $4 x^{2} - 5 x$ .

In 7xy + 5, we first obtain xy, multiply it by 7 to get 7xy. We add 5 to 7xy to get the expression 7xy + 5 .
In $x^{2} y$ , we first obtain $x^{2}$ by multiplying the variable x by itself and then multiply $x^{2}$ by y to obtain the expression $x^{2} y$ .

3. BASIC DEFINITIONS RELATED TO ALGEBRAIC EXPRESSIONS
I Term
Algebraic expressions contain one or more terms.
Terms contain letters and numbers connected by multiplication, division or powers.
We combine terms using addition to make expressions. For example, $4 x^{2}$ – xy is an expression with two terms, $4 x^{2}$ and (–xy).
II. Factors of a Term
When numbers and literals are multiplied to form a product then each quantity multiplied is called a factor of the product.
• A constant factor is called a numerical factor.
• A variable factor is called a literal factor.
Example:
• In 7ab, the numerical factor is 7 and literal factors are a, b and ab.
• In $- 9 x^{2} y$ , the numerical factor is –9 and the literal factors are $x, x^{2}, xy and x^{2} y$

II. Constant Term
A term of the expression having no literal factor is called the constant term.
Example: In the expression 3x – 7y + 5; the constant term is 5.
III. Coefficients
Any of the factors of a term is called the coefficient of the product of other factors. In particular, the constant part is called the numerical. Coefficient of the term and the remaining part is called the literal coefficient of the term.
Example: In the term –3xyz
Numerical coefficient = – 3
Literal coefficient = xyz
Coefficient of x = – 3yz
Coefficient of y = – 3xz
Coefficient of z = – 3xy
4. IDENTIFYING COEFFICIENT AND VARIABLE
Every term in an algebraic expression has a coefficient. The coefficient is the signed numerical part of a term in an algebraic expression that is, the number and the sign (+ or –) that goes with that term. For example, suppose you are working with the following algebraic expression: $- 4 x^{3} + x^{2} - x - 7$

The table below shows the four terms of this expression, with each term’s coefficient

Term	Coefficient	Variable
$- 4 x^{3}$	$- 4$	$x^{3}$
$x^{2}$	$1$	$x^{2}$
$- x$	$- 1$	$x$
$- 7$	$- 7$	none

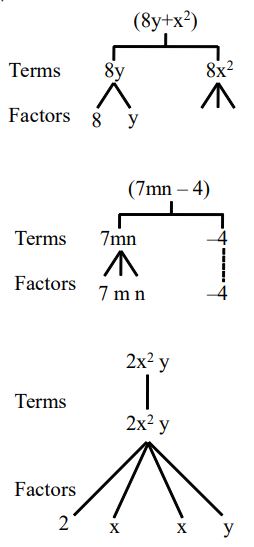
Identifying terms of an expression – Tree Diagram Method
Consider an expression : $8 y + 3 x^{2}, 7 m n - 4, 2 x^{2} y$
Let’s now identify the terms through a tree diagram .
We can represent the terms and factors of the terms of an expression by a tree diagram

5. CLASSIFICATION OF ALGEBRAIC EXPRESSIONS
I Monomial
An algebraic expression which contains one term is called a monomial.
Example: Each one of the expression $5 x, 12 x y, 3 a b^{2} c, - 5 z^{2}$ is a monomial.
II. Binomial
In algebraic expression which contains two terms is called a binomial.
Example: Each one of the expression $5 + 2 x, 1 - 7 x^{2} y z, a^{2} + y^{2}, b + \frac{1}{b}$ is a binomial.
III. Trinomial
An algebraic expression which contains three terms is called a trinomial.
Example: Each one of the expression 7x $7 x + 5 y - 8 z, 5 - a b c - a^{2} b, a^{2} + b^{2} - 2 a^{2} b$ is a trinomial.
IV. Multinomial
An algebraic expression containing two or more terms is called a multinomial.
Example: Each one of the expression x + 2y , x + 2y + 3z , x + 2y + 3z + 4w is a Multinomial.
Note: In general, an expression with one or more terms is called a polynomial. Thus, each of these is a polynomial.
Like and Unlike Terms :
The terms which have the same algebraic factors, are called like terms and the terms which have different algebraic factors are called unlike terms.
For example, the terms 3xy, – 5xy, 2xy etc. are called like terms whereas the terms 5px, 3yz, 4 etc. are called unlike terms.5 6 Mathematics
We should follow the following simple steps to decide whether the given terms are like terms
(i) Concentrate on the literal or algebraic part of the terms.
(ii) Check the variables in the terms. The terms should contain the same variables.
(iii) Check the powers of the variables. The powers of the variables must be the same.
Note : In deciding like terms, two things do not matter :

(A) the numerical coefficients and

(B) the order in which the variables occur in the terms.

6. ADDITION AND SUBTRACTION OF ALGEBRAIC EXPRESSIONS
I Addition
Add similar terms by adding their coefficients and keeping the same variable part. For example, suppose you have the expression 2x + 3x. Remember that 2x is just shorthand for x + x, and 3x means simply x + x + x. So when you add them up, you get the following: = x + x + x + x + x = 5x
As you can see, when the variable parts of two terms are the same, you add these terms by adding their coefficients: 2x + 3x = (2 + 3)x. The idea here is roughly similar to the idea that 2 apples + 3 apples = 5 apples.
You cannot add non-similar terms. Here are some cases in which the variables or their exponents are different.
2x + 3y
2yz + 3y
$2 x^{2}$ + 3x
In these cases, you cannot perform the addition. You are faced with a situation that is similar to 2 apples + 3 oranges. Because the units (apples and oranges) are different, you cannot solve the problem.
II. Subtraction
Subtraction works much the same as addition. Subtract similar terms by finding the difference between their coefficients and keeping the same variable part.
For example, suppose you have 3x – x. Recall that 3x is simply shorthand for x+ x + x. So doing this subtraction gives you the following.
x + x + x – x = 2x
No big surprises here. You simply find (3 – 1)x. This time, the idea roughly parallel the idea that Rs. 3 – Rs. 1 = Rs. 2.
Here is another example: 2x – 5x
Again, no problem, as long as you know how to work with negative numbers. Just find the difference between the coefficients: = (2 – 5)x = –3x
In this case, recall that Rs. 2 – Rs. 5 = Rs. –3 (that is, a debt of Rs. 3).

You cannot subtract non-similar terms. For example, you cannot subtract either of the following: 7x – 4y
$7 x^{2} y - 4 x y^{2}$
As with addition, you cannot do subtraction with different variables.
7. FINDING VALUES OF ALGEBRAIC EXPRESSIONS AT GIVEN POINTS
We know that the algebraic numbers represent numbers. Thus if the values of algebraic numbers is given, we can find the value of the given expression. For example, if x = 3, y = 5, then to find the value of the expression 2x + 3y, we put x = 3 and y = 5 in 2x + 3y.
$∴$ The required value of given expression = 2 (C) + 3 (5) = 6 + 15 = 21

8. FORMULAE AND THEIR USES
Formulae
We observe that equation A = $S^{2}$ is useful in easily solving many problems of the same type. Equation which are used frequently to solve problems are called formulae. Formulae state that relationship existing between two (or) more variables.
Subject of the Formulae
Formulae are frequently given with one variable standing alone on one side of the equality sign and the value of the variable given in terms of the others. This variable standing alone on one side its called “The subjects of the formula”

Expressing the Principles Stated in words in terms of Symbols
Formulae are time saving devices in this age of computerisation and quick decisions. Formulae that you have already learnt give the meaning of long statements, precisely in symbols.
Example: The statement that the area of a rectangular field is the product of its length and breadth expressed in symbol as A = l × b
Where ‘A’ is unit areas.
‘l’ and ‘b’ are units of length and breadth respectively
Stating Formula given Symbolically in Word Form
The ability to read a formula given in symbols and state in words, so that they can have proper understanding of the formula and apply it in correct situation.
Example:
(i) State the formula V = lbh in words. Volume of a rectangular parallelepiped is equal to the product of its length, breadth and height.
(ii) $A = \frac{1}{2} b h$ state the formula in words. Area of a triangle is equal to half the product of its base and height

Changing the Subject of the Formula
Average of a finite number of quantities is obtained by dividing the sum of the quantities by their number.
This is symbolically written in the form of formula as $a = \frac{s}{n}$

Where a = average, s = Sum of quantities, n = number of quantities.
In $a = \frac{s}{n},^{'} a^{'}$ is the subject of the formula.
This formula is useful to find the value of ‘a’, when the values of ‘s’ and ‘n’ are known. Suppose the values of ‘a’ and ‘n’ are given and ‘s’ is to be found. Then we have to change the formula in such a way that ‘s’ is given in terms of ‘a’ and ‘n’ (or) ‘s’ is the subject of the formula . $a = \frac{s}{n}$

Multiplying both sides by ‘n’ $\Rightarrow a \times n = \frac{s}{n} \times n; a \times n = s (or) s = a n$

This new formula is deduced from the original formula. $a = \frac{s}{n}$

i.e., the subject ‘a’ is changed (or) transformed to subject ‘s’. This type of transformation is useful in deriving other forms (or) variants of the same formula. These new formula are derived (or) auxilary formulae.
The following characteristics of subject in a formula have to be noted;
• The subject symbol occurs on the left side of the equality sign.
• It is written independently without being linked with any other quantities (or) variables
• Its coefficient is always one.
• All properties used in solving simple equations are also used in transforming the subject of a formula

Framing a Formula
To express a given statement in the form of an equation by using literals and mathematical symbols is called framing the formula
Example:
(i) The rule that the perimeter (p) of a rectangle is twice, the sum of its length ( $l$ ) and breadth (b), is given by the formula p = 2( $l$ + b).
(ii) The rule that the volume (v) of a cube is equal to the cube of the length of its edge(a), is given by the formula; $V = a^{3}$
(iii) The rule that the centigrade temperature (C) is equal to five-ninths of the difference between fahrenheit (F) and 32, is given by the formula. $C = \frac{5}{9} (F - 32)$
(iv) A number decreased by 3, is divided by 2 to get 4. This fact may be expressed in the form of an equation as $\frac{x - 3}{2} = 4$ , where ‘x’ is the number.
(v) If ‘5’ is added to both the numerator and the denominator of a certain fraction, its value is 1/4. This fact is given by the formula $\frac{x + 5}{y + 5} = \frac{1}{4}$ . Where ‘x’ is the numerator and ‘y’ is the denominator of the fraction

Need Help?