1. FACTORS AND MULTIPLES
1. Multiples
The numbers obtained by multiplying the given number with a natural number are called multiples of a given number.
Example:
and so on. Therefore 2, 4, 6, 8….etc are called multiples of 2. 3,6,9,12,15……etc. are called multiples of 3.
Note:
(i) Every number is a multiple of itself.
(ii) Every number is multiple of one. Since .
(iii) There are infinite number of multiples for a natural number.
(iv) When a number divides another number exactly, then dividend is called a multiple of the divisor.
For example, 16 is exactly divisible by 4. Here 16 is dividend and 4 is divisor. 16 is multiple of 4 (since 4×4 = 16)
(v) When two or more numbers are multiplied, then the product is a multiple of each number.
Example:
; 24 is multiple of 2, 3, 4
is multiple of 4, 5
(vi) For every number, number itself is a least multiple.
Example:
2,4,6,8….are multiples of 2, among these multiples 2 is a least multiple of 2.
(vii) The greatest multiple of a number does not exist, since the multiples of a number are products of number with natural numbers and set of natural numbers are infinite.
(vii) For two or more numbers, the multiples which are common to both numbers are called common multiples. i.e., for any two numbers a, b; a b = ab. The product of ‘ab’ is common multiple of
both ‘a’ and ‘b’
Example:
2 × 3 = 6; 6 is common multiple of 2 and 3 (since the multiples of 2 are 2, 4, 6, 8 etc., and the multiples of 3 are 3, 6, 9, 12 etc.,)
2. Factors
For any two numbers a,b; if ‘ab’ is the product of a, b then each of a, b are called factors of product ab.
Example:
2 × 3 = 6, where 2, 3 are factors of product 6.
When a number divides another number exactly (it means it leaves remainder 0); then the divisor is called a factor of the dividend.
Example:
2 divides 18 and leaves a remainder 0. i.e., 2 divides 18 exactly. Therefore 2 is a factor of 18, where 2 is divisor and 18 is dividend.
When two or more numbers are multiplied then each number is a factor of the product.
Example:
2 × 3 × 4 = 24 where 2, 3, 4 are called factors of 24
1 × 12 = 12, 2 6 = 12, 3 × 4 = 12. Therefore 1, 2, 3, 4, 6, 12 are factors of 12
Note:
(i) We denote the set of all factors of ‘n’ by F(n) or .
Example: F(12) = = {1,2,3,4,6,12}
(ii) The smallest factor of any number is 1 and the largest factor is the number itself.
Example:
1, 2, 3, 4, 6, 12 are factors of 12. Among these factors, the smallest factor is 1 and the greatest (or larger) factor is 12.
(iii) 1 is a factor of every number and is a smallest factor
(iv) Every number is a factor of itself and is largest factor.
(v) The factor of a number is less than or equal to that number.
Example:
The factors 12 are less than are equal to 12 (since 1 < 12, 2 < 12, 3 < 12, 4 < 12, 6 < 12, 12 12)
2. PRIME AND COMPOSITE NUMBERS
Even Numbers
All the whole numbers which are exactly divisible by 2 are called even numbers.
Example:
0, 2, 4, 6, 8,10, 12, …………….. are even numbers (as each is exactly divisible by2). There are infinite even numbers.
Odd Numbers
All the whole numbers which are not exactly divisible by 2 are called odd numbers.
Example:
1, 3, 5, 7, 9, 11, …………. are odd numbers (as each is not exactly divisible by 2). There are infinite odd numbers.
Prime Numbers
Natural numbers which have exactly two distinct factors (1 and the number itself) are called Prime numbers.
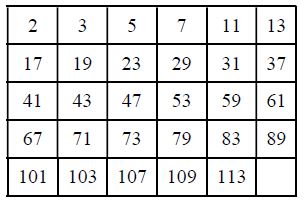
The natural numbers 2, 3, 5, 7, 11, 13, 17, 19, …… are some prime numbers.
(A) There are infinite prime numbers.
(B) 2 is the only prime number which is even. All other prime numbers are odd.
(C) Every odd number is not prime.
For example 9, 15, 21, ……. are odd numbers, but not prime numbers.
Composite Numbers
Natural numbers which have more than two factors (at least one more factor other than 1 and the number itself) are called composite numbers.
The natural numbers 4, 6, 8, 9, 10, 12, 14, 15, 16, ….. are some composite numbers.
(A) There are infinite composite numbers.
(B) 1 is neither prime nor composite. It is called unity.
(C) All even numbers (except 1) is either prime or composite.
(D) All even numbers (except 2) are composite numbers.
(E) Some odd numbers are composite and some are prime.
Methods of finding Prime Numbers
Method 1:
To find prime numbers between 1 and 100 Eratosthenes, a Greek mathematician devised a simple method.
Procedure:
Write down the numbers from 1 to 100 in rows of ten.
Cross out 1.
Encircle 2 and cross out all the multiples of 2 i.e., 4, 6, 8….etc
Encircle 3 and cross out all the multiples of 3. i.e., 6, 9, 12, 15, 18, 21 etc.
Encircle 5 and cross out all the multiples of 5 i.e., 10, 15, 20, 25….etc
Encircle 7 and cross out all the multiples of 7 i.e., 14, 21, 28….etc
Now encircle each one of remaining numbers and cross out all the multiples of all of them if exist.
Continue this process till all the numbers in the list are either encircled or crossed out. Now the encircled numbers are the Prime Numbers and all the crossed out numbers are Composite Numbers. Thus we get 25 prime numbers between 1 and 100. The tabular arrangement of numbers obtained below is named as sieve of eratosthenes.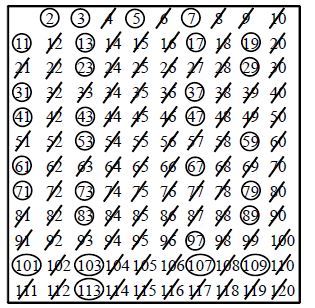
Method 2:
To test a number ‘n’ whether it is prime or not, take the square root of ‘n’ and consider as if it is a natural number; otherwise just increase the square root of it to the next natural number. Then divide the given number by all the prime numbers less than the square root obtained for that number. If the number is divisible by any of these prime numbers then it is not a prime number else it is a prime number.
Example:
Check that whether 241 is prime.
When we take the square root of 241 it is approximated to 16, so we consider it 16. Now divide 241 by all the prime numbers below 16 are 2, 3, 5, 11, 13.Since 241 is not divisible by any one of the prime numbers below 16, it is a prime number.
Note:
(i) The number of prime numbers between 1 to 10 is 4
(ii) The number of prime numbers between 11 to 20 is 4
(iii) The number of prime numbers between 21 to 30 is 2
(iv) The number of prime numbers between 31 to 40 is 2
(v) The number of prime numbers between 41 to 50 is 3
(vi) The number of prime numbers between 51 to 60 is 2
(vii) The number of prime numbers between 61 to 70 is 2
(viii) The number of prime numbers between 71 to 80 is 3
(ix) The number of prime numbers between 81 to 90 is 2
(x) The number of prime numbers between 91 to 100 is 1
(xi) The number of prime numbers between 101 to 110 is 4
(xii) The number of prime numbers between 111 to 120 is 1
The Number of Prime Numbers between 1 to 100 is 25
Co-Prime Numbers
Two natural numbers are said to be co-prime numbers (or relatively prime numbers) if they have only 1 as common factor.
Example:
2, 3 ; 2, 5 ; 3, 10; 15, 16 ; ….. are co-prime numbers.
Twin Primes
Two prime numbers which have only one composite number between them are called twin primes.
Example:
3, 5, ; 5, 7 ; 11, 13; 17, 19 ; 29, 31; 41, 43; 59, 61 ; 71, 73; …… are twin primes.
Perfect Number
If the sum of all the factors of a number is two times the number, then the number is called a perfect number.
Example:
Factors of 6 are 1, 2, 3 and 6. Sum of all the factors = 1 + 2 + 3 + 6 = 12 = 2(6)
6 is a perfect number.
3. COMMON FACTORS AND COMMON MULTIPLES
Common factors
Observe the factors of some numbers taken in pairs.
(A) What are the factors of 4 and 18?
The factors of 4 are 1, 2 and 4.
The factors of 18 are 1, 2, 3, 6, 9 and 18.
The numbers 1 and 2 are the factors of both 4 and 18.
They are the common factors of 4 and 18.
Common multiples
What are the multiples of 4 and 6?
The multiples of 4 are 4, 8, 12, 16, 20, 24, … (write a few more)
The multiples of 6 are 6, 12, 18, 24, 30, 36, … (write a few more)
Out of these, are there any numbers which occur in both the lists?
We observe that 12, 24, 36, … are multiples of both 4 and 6.
Can you write a few more?
They are called the common multiples of 4 and 6.
4. TESTS FOR DIVISIBILITY OF NUMBERS
I. Divisibility by 2.
A natural number is divisible by 2 if its units digit is 0, 2, 4, 6 or 8 (i.e. unit’s digit is divisible by 2)
II. Divisibility by 3.
A natural number is divisible by 3 if the sum of its digits is divisible by 3.
III. Divisibility by 4
A natural number is divisible by 4 if the number formed by its last two (i.e. ten’s and unit’s) digits is divisible by 4.
IV. Divisibility by 5
A natural number is divisible by 5 if its last (unit’s) digit is 0 or 5.
V. Divisibility by 6.
A natural number is divisible by 6 if it is divisible by 2 as well as by 3.
VI. Divisibility by 8.
A natural number is divisible by 8 if the number formed by its last three (Hundred’s, ten’s and unit’s) digits is divisible by 8.
VII. Divisibility by 9.
A natural number is divisible by 9 if the sum of its digits is divisible by 9.
VIII. Divisibility by 10.
A natural number is divisible by 10 if its last (unit’s) digit is 0.
IX. Divisibility by 11.
A natural number is divisible by 11 if the difference of the sums of digits at the alternative places (starting from unit’s place) is divisible by 11.
Some observations
(A) All numbers divisible by 2 are even.
(B) Numbers divisible 3 may be even or odd.
(C) Numbers which are divisible by 2 and 3 are divisible by 6.
(D) Numbers which are divisible by 4 are also divisible by 2.
(E) Numbers which are divisible by 8 are also divisible by 2 and 4.
(F) Numbers which are divisible by 9 are also divisible by 3.
(G) Numbers which are divisible by 10 are also divisible by 2 and 5.
5. PRIME FACTORIZATION
We are familiar with the terms factors and multiples. So let us factorise 36 in different ways as:
36 = 1 × 36, 36 = 2 × 18, 36 = 3 × 12,
36 = 4 × 9, 36 = 6 × 6,
36 = 2×2×9, 36 = 2 × 6 × 3,
36 = 3×3×4, 36 = 2 × 2 × 3 × 3,
Here we observe that when we factorise 36 = 2×2×3×3, then all its factors are primes. Such factorisation of a number is called prime factorisation.
Thus if a natural number is expressed as the product of prime numbers, then the factorisation of the number is called its prime factorisation.
6. HIGHEST COMMON FACTOR
H.C.F. of two or more natural numbers is the largest (or highest) common factor (or divisor) of the given numbers.
Thus, H.C.F. is equal to the greatest element of the set of common factors (or divisors) of the given numbers. Therefore it is also called Greatest Common Divisor (G.C.D.)
Note:
H.C.F. of two or more numbers divides each number completely.
Methods of finding H.C.F.
I. Continuous Division Method
In continuous division method, we divide the larger number by the smaller number and get a remainder.
Then we divide the first divisor by the remainder and get a new remainder. Continue this process till
the last remainder is zero. The last divisor in this process is the H.C.F. of the given two numbers.
Example: Find the HCF of 180 and 324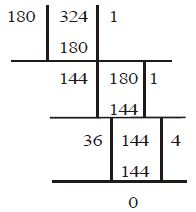
HCF of 180 and 324 is 36.
To find the H.C.F. of three or more numbers, we proceed as:
i) Find the H.C.F. of any two given numbers.
ii) Find the H.C.F. of the third number with the H.C.F. of step (i).
iii) H.C.F. obtained in step (ii) is the required H.C.F. of the three given numbers.
iv) For more numbers, we continue this process.
Example: Find the HCF of 24, 32 and 44.
First consider 24 and 32.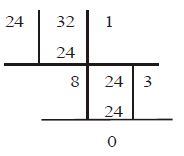
Now, consider 8 and 44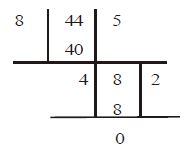
HCF of 24, 32 and 44 = 4
II. Prime factorisation method
In prime factorisation method, we find the prime factorisation of each of the given numbers. Then H.C.F. is equal to the product of all the different common prime factors of the given numbers using each common factor the least number of times it appears in the prime factorisation of all of the given numbers.
Example: Find the HCF of 60 and 216.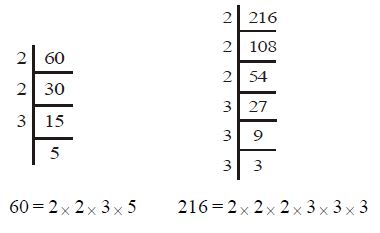
7. LOWEST COMMON MULTIPLE
L.C.M. of two natural numbers is equal to the smallest natural number which is a multiple of both the numbers.
Thus, L.C.M. is equal to the smallest element of the set of common multiples of the given natural numbers.
Example: Find the LCM of 6 and 12.
Multiples of 6 = {6, 12, 18, 24, 30, 36,……..}
Multiples of 12 = {12, 24, 36, …………..}
Set of common multiples 6 and 12 = {12, 36, …}
The smallest element of this set = 12
LCM = 12
I. Methods of finding L.C.M. Division Method
In division method, we divide the given numbers by a common divisor of at least two of the given numbers and write the numbers as they are which are not divisible by this common divisor. We continue this process till no two numbers have a common factor. Then L.C.M. of the given numbers is the product of the divisors and the remaining numbers.
Example: Find the LCM of 336 and 420
LCM = = 1680
II. Relation between H.C.F. and L.C.M. of two Natural Numbers
Product of H.C.F.and L.C.M. of two natural numbers is equal to the product of the two numbers.
H.C.F. L.C.M. = Product of the two numbers.








