Basic Geometrical Ideas

1. INTRODUCTION

Geometry is all about shapes and their properties.
Geometry can be divided into:
Plane Geometry
Plane Geometry is about flat shapes like lines, circles and triangles … shapes that can be drawn on a piece of paper
Solid Geometry
Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres.

2. POINTS
A point is a mark of position. A fine dot represents a point. We denote a point by a capital letter A, B, P, Q etc. A point has no length, breadth or thickness.

3. A LINE SEGMENT
The straight path between two points A and B is the line segment AB, represented as $\overline{\mathrm{AB}}$ .
The points A and B are called its end points.
A line segment has a definite length.

The distance between two points A and B gives the length of the line segment $\overline{\mathrm{AB}}$ .
4. A LINE
A line segment AB when extended indefinitely in both the directions is called line $\overleftrightarrow{\mathrm{AB}}$.

A line has no end points. A line has no definite length. A line cannot be drawn, it can simply be represented on the plane of a paper.
Incidence Axioms on Lines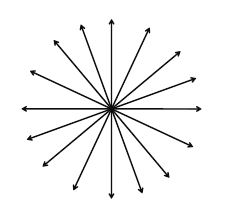

• A line contains infinitely many points
• An infinite number of lines can be drawn to pass through a given point
• One and only one line can be drawn to pass through two given points A and B.

Collinear Points
Three or more points are said to be collinear, if there is a line which contains them all.

In the above figure; P, Q, R are collinear points.

5. INTERSECTING LINES
Two lines having a common point are called intersecting lines. The point common to two given lines is called their point of intersection. In the figure, the lines AB and CD intersect at a point O.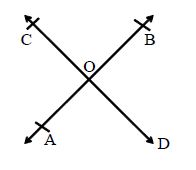

6. PARALLEL LINES
Two lines l and m in a plane are said to be parallel, if they have no point in common and is written as l || m. The distance between two parallel lines always remains the same.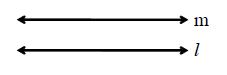

7. RAY
A line segment AB when extended indefinitely in one direction is the ray $\overrightarrow{\mathrm{AB}}$ .
It has one end point A.

A ray has no definite length. A ray cannot be drawn, it can simply be represented on the plane of a paper.

8. CURVES
Curves can be defined as figures that flow smoothly without a break. A line is also a curve, and is called a straight curve.
Simple curves
Curves that do not intersect themselves are called simple curves.

Open curves
Curves whose end points do not meet are called open curves.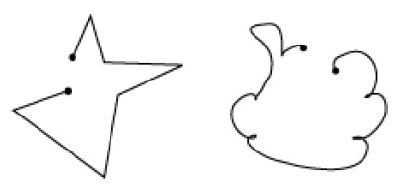

Closed curves
Curves whose end points join to enclose an area are called closed curves.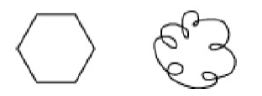

For a closed curve, we can identify three regions: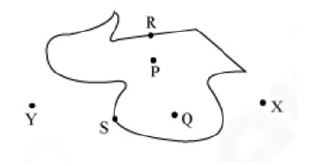

The interior of the curve: These points are in the interior of the closed curve.
Boundary of the curve: These points are on the boundary of the closed curve.
Exterior of the curve: These points are in the exterior of the closed curve.
The interior of a curve together with its boundary is called its “region”.

9. POLYGONS
Simple closed curves made up of only line segments are called polygons. Line segments that form the polygon are the sides of the polygon. Any two sides with a common end point are called the adjacent sides. The point of intersection of a pair of sides is called a vertex. The end points of the same side are adjacent vertices. The line segment joining any two non-adjacent vertices of a polygon is a diagonal. ABCDEF is a polygon.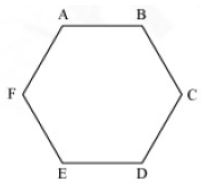

The line segments AB, BC, CD, DE, DF, and FA are known as the sides of the polygon ABCDEF.
Any two sides with common end points are called adjacent sides. AB and BC are adjacent sides with common end point B.
The meeting point of a pair of sides of a polygon is known as vertex. In the polygon ABCDEF, sides AB and BC meets at point B. So, point B is called the vertex of the polygon. Similarly, the other vertices are A, C, D, E, and F.
The line joining any two non-adjacent vertices of a polygon is known as its diagonal. In the following polygon ABCDEF, the diagonals are AC, AD, AE, BD, BE, BF, CE, CF, and DF.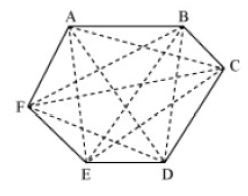

10. ANGLES
An angle is made up of two rays starting from a common end point.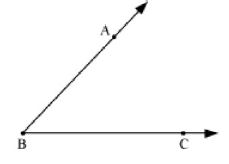

In this figure $\overrightarrow{\mathrm{BA}}$ and $\overrightarrow{\mathrm{BC}}$ rays have one common end point, that is, B. The rays $\overrightarrow{\mathrm{BA}}$ and $\overrightarrow{\mathrm{BC}}$ are called the arms or sides of the angle. The common end point B is the vertex of the angle.
We name the above angle as $\angle$BAC.

11. TRIANGLES
A polygon made up of three line segments is called a triangle.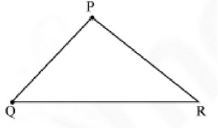

The triangle in the diagram is $∆$PQR. Points P, Q and R are the vertices. $\overline{\mathrm{PQ}}$ , $\overline{\mathrm{QR}}$ and $\overline{\mathrm{RP}}$ are the sides, and $\angle$PQR, $\angle$QRP, $\angle$RPQ are the angles of the triangle. A triangle has an interior and exterior.

12. QUADRILATERALS
A quadrilateral is a four-sided polygon.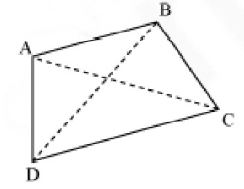

AC and BC are the diagonals of quadrilateral ABCD. $\angle$A and $\angle$C, and $\angle$B and $\angle$D are the opposite angles. $\angle$B and $\angle$C are the adjacent angles. Similarly, the other adjacent angles are $\angle$A and $\angle$B, $\angle$C and $\angle$D, $\angle$D and $\angle$A.

13. CIRCLES
A circle is formed by a point moving at the same distance from a fixed point. The fixed point is the centre of the circle. A circle is also a simple closed curve however, it does not have any sides or angles.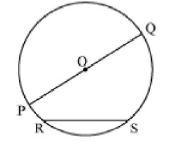

The fixed point O is the centre of the circle.
The fixed distance OP = OQ is the radius of the circle.
The distance around the circle is its circumference.
Circumference
The line that forms the boundary of a circle is called its circumference. The part enclosed by the circumference of a circle is called the interior of the circle. The part left outside the circle is said to be the exterior of the circle. Some points may lie on the circumference of the circle.
Radius
A line segment that joins the centre of the circle and a point on the circumference is called the radius of the circle. The radius of a circle is half of the diameter.
Chord
A chord is a line segment joining two points that lie on a circle.
Diameter
A chord passing through the centre of the circle is called its diameter. A diameter is the longest chord of a circle.
Arc
An arc is a part of the circumference of a circle.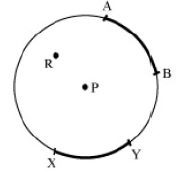

Sector
The part of a circle enclosed by two radii and an arc is called a sector.
Segment
The part of a circle that is enclosed by a chord and an arc is called a segment of the circle.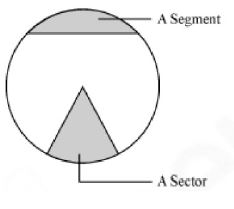

Semi-circle
A diameter of a circle divides it into two halves. Each half is called a semi-circle.