Whole Numbers

1. WHOLE NUMBERS
I. Successors and Predecessors of Numbers
Successor
“If 1 is added to any natural number, then we obtain the successor of that number.”
For example, the successor of 11 will be 11 + 1 = 12.
Predecessor “If 1 is subtracted from any natural number, then we obtain the predecessor of that number.”
For example, the predecessor of 11 will be 11 – 1 = 10.
Note
1. Every natural number has a successor because there is no largest natural number.
2. Successor and predecessor are reverse of each other.
For example, 20 is the successor of 19 and 19 is the predecessor of 20.
3. Every number except 1 has a predecessor in case of natural numbers. This is because 1 – 1 = 0 and 0 is not a natural number. It is a whole number.
Whole numbers
“If zero is added to the collection of natural numbers, we obtain the collection of whole numbers, or in other words, we can say that all natural numbers along with zero are called whole numbers.”
Whole numbers are a set of numbers starting from 0, that is 0, 1, 2 …
Therefore, the natural number 1 has a predecessor 0 which is a whole number.
Remember: All natural numbers are whole numbers but all whole numbers are not natural numbers.

2. NUMBER LINE
We know what whole numbers are. These numbers can be represented on a line, which is called the number line. We can use this number line to determine whether a number is greater or lesser than another given number.
Example
Mark the successor of 10 and the predecessor of 15 on the number line and compare them. Also find the distance between them.
Solution
The successor of 10 is 11. The predecessor of 15 is 14.
Now, we locate these two points on the number line as follows.

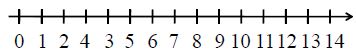
Since the number 14 is on the right of 11, therefore,
The distance between 11 and 14 is 3 units.
Example
Locate the unknown points on the following number line.

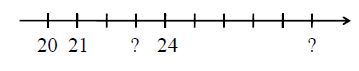
Solution
The first unknown point is 2 units away from 21. Therefore, it is 23.
The second unknown point is 5 units away from 24. Therefore, it is 29.
Addition, Subtraction and Multiplication on a Number Line
Do you know that basic mathematical operations such as addition, subtraction, and multiplication can
be carried out on a number line? It requires a good understanding of the number line. Let us now solve
some examples to understand the concept.
Example
Add 6 and 7 on the number line.
Solution
Since the first number is 6, we mark the position of number 6 on the number line.

Since the number to be added is 7, we move seven units to the right of number 6 on the number line.
This can be done as follows.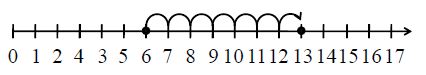

Since the final position obtained on the number line is 13, we obtain 13 by adding 6 and 7.
Example
Subtract 9 from 16 using the number line.
Solution:
We have to find the value of the expression 16 – 9 on the number line.
Mark the number 16 on the number line. From this point, jump nine units to its left. Since the final position obtained on the number line is 7, the value of the expression (16 – 9) is 7.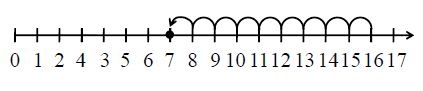

Example
Multiply 5 with 3 on the number line.
Solution:
The first number is 5. Since the number to be multiplied is 3, we will start from zero and make 3 jumps of 5 units each. This can be done as follows.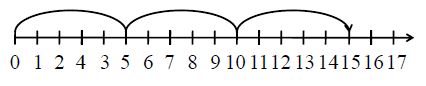

Since the final position obtained on the number line is 15, the value of the expression 5 × 3 is 15.

3. PROPERTIES OF WHOLE NUMBERS
I. Addition Properties
Closure Property
For any two whole numbers a and b; their sum (a + b) is also a whole number. This is called closure property of addition.
Example: 5 + 6 = 1. 1 is a whole number
Commutative Property
For any two whole numbers a and b; when added in any order gives the same sum i.e., a + b = b + a.
This is called commutative property of addition.
Example: 2 + 3 = 3 + 2 = 5
Associative Property
For any three whole numbers a, b, c; a + (b + c) = (a + b) + c. This is called associative property of addition.
Example: 2 + (3 + 4) = (2 + 3) + 4 = 9
Additive Identity
For every whole number a; a + 0 = 0 + a = a. 0 is called the additive identity.
Example: 2 + 0 = 0 + 2 = 2
II. Multiplication Properties
Closure Property
For any two whole numbers a and b; their product a b is also a whole number. This is called closure property of multiplication.
Example: 2$\times$ 3 = 6. 6 is also a whole number.
Commutative Property
For any two whole numbers a, b; a$\times$b = b$\times$a
Example: 4$\times$5 = 5$\times$4 = 20
Associative Property
For any three whole numbers a, b, c; $a\times (b\times c)=(a\times b)\times c$
Example: 2 $\times$(3$\times$5) = (2$\times$3)$\times$5 = 30
Multiplicative Identity
For any whole number a; $\mathrm{a}\times 1=1\times \mathrm{a}=\mathrm{a}$. Here 1 is called the multiplicative identity in the set of all whole numbers.
Note:
The whole number when multiplied by zero, the product is always zero, i.e., for any whole number a;
$\mathrm{a}\times 0=0\times \mathrm{a}=0$. This is called zero property in multiplication of whole numbers.
For any two whole numbers a, b; if a b = 0, then either a = 0 or b = 0 or a = b = 0.
Distributive Property of Multiplication over Addition
For any three whole numbers a, b, c; $a\times (b+c)=(a\times b)+(a\times c)\text{ or }(b+c)\times a$a = $(b\times a)+\left(c\times a\right)$
Example:
$2\times (3+4)=(2\times 3)+(2\times 4)=14$
$(3+4)\times 5=(3\times 5)+(4\times 5)=35$
III. Properties of Subtraction
Closure Property
For any two whole numbers a, b; (a – b) may not be a whole number. Therefore closure property is not true for subtraction of whole numbers.
Example: 2 – 4 = –2. –2 is not a whole number.
Commutative Property
For any two whole numbers a, b; a – b$\ne$b – a. Therefore subtraction of whole numbers is not commutative.
Example: 2 – 4 = –2 and 4 –2 = 2 but –2$\ne$2
Associative Property
For any three whole numbers a, b, c; (a – b) – c$\ne$a – (b – c). Therefore subtraction is not associative in whole numbers
Example: (2 – 3) – 5 = –6 and 2 – (3 – 5) = 4 but – 6$\ne$4
Note: Subtractive identity does not exist since there is no ‘e’ such that a – e = e – a = a.
IV. Properties of Division
Closure Property
Quotient of any two whole numbers need not always be a whole number. Hence division is not
closure in whole numbers.
Example: $\frac{2}{5}$= 0.4 is not a whole number.
Commutative Property
For whole numbers a, b; $\frac{a}{b}\ne \frac{b}{a}$ where a$\ne$b. Hence division of whole numbers is not commutative.
Example: $\frac{2}{3}\ne \frac{3}{2}$(since $\frac{2}{3}$= 0.66, $\frac{3}{2}$= 1.5)
Associative Property
For any three whole numbers a, $b(\ne 0), c(\ne 0); (a÷b)÷c\ne a÷(b÷c)$. Hence division of whole numbers is not associative.
Example: $(4÷2)÷2=1$
$4÷(2÷2)=4$
Therefore $(4÷2)÷2\ne 4÷(2÷2)$
If any whole number is divided by 1, the quotient is the same number i.e., for any whole number a; a$÷$1 = a but 1$÷$a$\ne$a.
Therefore 1 is not a division identity just it is one side operation.
Note: Division is an inverse operation to multiplication.
Example: 18$÷$2 = 9
9 × 2 = 18
Therefore for any whole number $a(\ne 0),b,\times b÷a=x\Rightarrow a\times x=b$
Division by Zero
There is no whole number which when multiplied by zero will ever give a non zero whole number i.e.,
there is no b$\in$W, such that $a\times 0=b. b÷0$ is not defined
Therefore the division of a whole number by zero is not defined.
Example: 2$÷$0 , 3$÷$0 are not defined
Division of Zero by Zero
Suppose 0$÷$0 = a; since division is inverse operation of multiplication, 0 a = 0 but whatever the whole number ‘a’ is; 0 a is always zero.
Example: $2\times 0=3\times 0=4\times 0$ = ………. = 0
Hence there does not exist a particular whole number such that 0 x a = 0, hence division by zero is not defined.
$\boxed{0 ÷ 0 is not defined}$
When zero is divided by any non-zero whole number, the quotient is always zero.
If 0 ÷ 2 = a, then 2 × a = 0$\Rightarrow$a = 0 (since a × b = 0$\Rightarrow$either a = 0 or b = 0 or a = b = 0)
The Division Algorithm
If a and b are any whole numbers with b $\ne$ 0, then there exist unique whole numbers q and r such that
$\mathrm{a}=\mathrm{bq}+\mathrm{r},\text{ where }0\le \mathrm{r}<\mathrm{b}$.
Here b is called the divisor, q is called the quotient, and r is the remainder. Notice that the remainder is always less than the divisor. Also, when the remainder is 0, this result coincides with the usual definition of whole number division.

4. PATTERNS IN WHOLE NUMBERS
Different whole numbers have different patterns. Whole numbers can be represented through dots as lines, triangles, squares, pentagons, hexagons and so on. For example:

Patterns with numbers are useful for verbal calculations. It takes lesser time as compared to actual calculations.
For example, we can calculate 11 × 991 as:
11× 991 =11×(l0009)
= 11 × 1000 -11 × 9 (Distributive) = 11000-99 = 10901.