1. PERIMETER
Closed Figure
A figure with no open ends is a closed figure.
Regular closed figures: A closed figure in which all the sides and angles equal.
Perimeter
Perimeter is the distance covered along the boundary forming a closed figure when we go round the figure once. The concept of perimeter is widely used in real life.
Eg:
• For fencing land.
• For building a compound wall around a house.
The perimeter of a regular closed figure is equal to the sum of its sides.
Perimeter of a Rectangle
= Length (l) + Breadth (b) + Length (l) + Breadth (b)
= 2(l + b)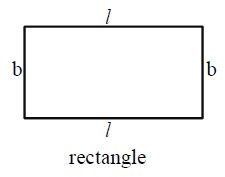
Perimeter of a Square
= s + s + s + s
= 4 × s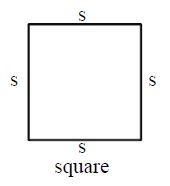
Equilateral Triangle:
A triangle with all its sides and angles equal is called an equilateral triangle.
The perimeter of an equilateral triangle with the side ‘a’ = a + a + a
= 3 × a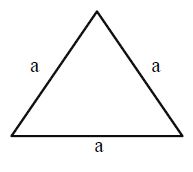
2. AREA
The amount of surface enclosed by a closed figure is called its area. The following conventions are to be adopted while calculating the area of a closed figure using a squared or graph paper.
1. Count the fully-filled squares covered by the closed figure as one square unit or unit square each.
2. Count the half-filled squares as half a square unit.
3. Count the squares that are more than half-filled as one square unit.
4. Ignore the squares filled less than half.
For example, the area of this shape can be calculated as shown: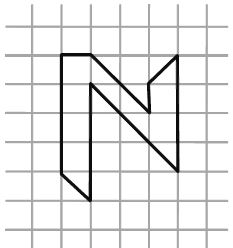
|
Covered area |
Number |
Area estimate (sq. units) |
|
Fully filled squares |
6 |
6 |
|
Half-filled squares |
6 |
7 ½ |
|
Squares filled more than half |
7 |
0 |
|
Squares filled less than half |
0 |
0 |
Area covered by full sq uares = 6 x 1 = 6 sq. units Area covered by half squares = 7 x ½ = 7/2= 3 ½ sq.units
Total area of the given shape = 6 + 3 ½ sq. units Thus, the total area of the given shape = 9 ½ sq.units
Area of a rectangle can be obtained by multiplying length by breadth. Area of the square can be obtained by multiplying side by side.
3. PERIMETER AND AREA OF PLANE FIGURES
Triangle
The closed figure obtained by joining three non collinear points is called a triangle.
Let a, b, c lengths of sides triangle then s = a + b + c is a perimeter of triangle, is called semi perimeters of the triangle
Equilateral Triangle
A triangle which is having equal sides is called an equilateral triangle.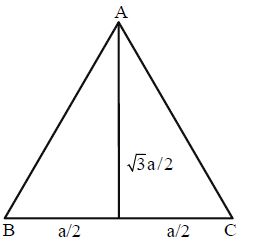
Let the side of an equilateral triangle be ‘a’ then height of equilateral triangle =
Perimeter of equilateral triangle = 3a units.
Area = base × height
Right Angle Triangle
In a triangle ABC if one angle is , then it is called a right angled triangle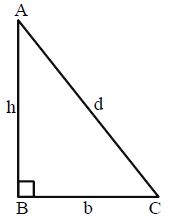
Note: If ABC is a Right Angled Triangle then by Pythagoras Theorem
Perimeter of right angled triangle = b + h + d
Area = base × height =
Acute-Angle Triangle
The triangle which is having all angles less than is called an acute angle triangle.
Obtuse Angled Triangle:
In a triangle one angle is above , then it is called an obtuse angle triangle.
Quadrilaterals
Rectangle
The quadrilateral which is having pair of equal and parallel opposite sides and one angle is .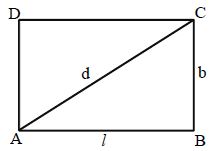
Let ABCD be a rectangle of length = l units, breadth = b units, diagonal = d units.
• Perimeter of the rectangle = 2(l + b) units
• Area = l × b units
• Area (A) =
• Diagonal (d) =
Square
The rectangle which is having all sides equal, all angles are right angles is called Square.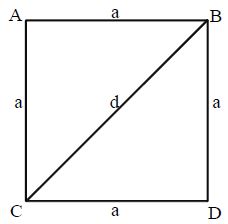
Let the side length of a square be ‘a’ units, then
• Perimeter of square = 4a units
• Diagonal of the square = units
• Area of the square = sq.units
• Area of the square = sq.units, where ‘d’ is length of diagonal
• Side of square = units
Rectangular paths
The path obtained between outer rectangular and inner rectangular fields is called Rectangular path.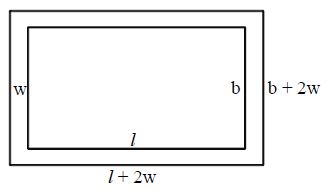
If ‘l’, ‘b’ are length and breaths of inner rectangle and ‘w’ be width of path then
• Length of outer rectangle = l + 2w
• Breadth of outer rectangle = b + 2w
• Area of inner rectangle = lb
• Area of outer rectangle = (l + 2w) (b + 2w)
• Area of path = (l + 2w) (b + 2w) – lb = 2(l + b)w + 4
Parallelogram
A quadrilateral in which both the pairs of opposite sides are parallel is called a parallelogram.
The perimeter of a parallelogram is twice the sum of the lengths of the adjacent sides.
In the below figure, the perimeter of parallelogram ABCD = 2(AB + BC)
The area of a parallelogram is the product of its base and perpendicular height or altitude.
Any side of a parallelogram can be taken as the base. The perpendicular dropped on that side from the opposite vertex is known as the height (altitude).
In the below figure, the area of parallelogram ABCD = AB × DE or AD × BF.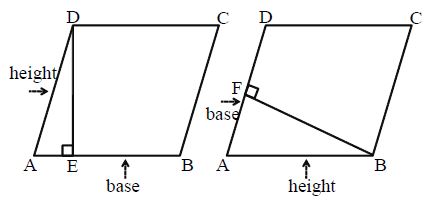
A parallelogram in which the all sides are equal is called a rhombus.
The perimeter and area of a rhombus can be calculated using the same formulae as that for a parallelogram.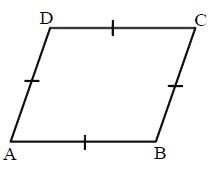
Circle
A circle is defined as a collection of points on a plane that are at an equal distance from a fixed point on the plane. The fixed point is called the centre of the circle.
Circumference: The distance around a circular region is known as its circumference.
Diameter: Any straight line segment that passes through the centre of a circle and whose end points are on the circle is called its diameter.
Radius: Any line segment from the centre of the circle to its circumference.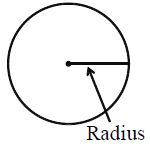
Circumference of a circle = 2r , Circumference of a circle = d, where r is the radius of the circle or, where d is the diameter of the circle.
is an irrational number, whose value is approximately equal to 3.14.
Circumference = Diameter 3.14
Diameter(d) is equal to twice radius(r): d = 2r
Circles with the same centre but different radii are called concentric circles.
The area of a circle is the region enclosed in the circle.
The area of a circle can be calculated by using the formula:
r2 , if radius r is given , if diameter D is given
, if circumference C is given 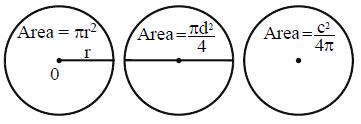
4. VOLUME AND SURFACE AREA OF CUBOID AND CUBE
Cuboid
A solid bounded by six rectangular plane faces is called cuboid
The net belonging to cuboid is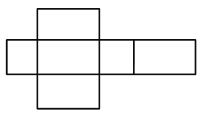
• Number of edges = 12
• Number of vertices = 8
• Number of faces = 6 flat rectangular faces
Cube
The cuboid whose length, breadth and height are equal is called a cube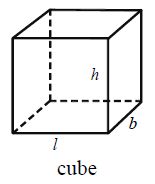
The nets belonging to cube is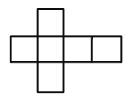
• Number of edges = 12
• Number of vertices = 8
• Number of faces = 6 flat square faces
Volume
The space occupied by a solid body is called its volume.
The units of volume are cubic millimetres () or cubic centimetres (cm)3 or cubic metre (m)3 etc…..
Volume and Surface Area of Cuboid
A solid bounded by six rectangular plane faces is called cuboid.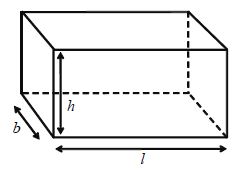
Let the Dimensions of cuboid be length = ‘l’ units, breath = ‘b’ units, height = ‘h’units, then
• Diagonal of cuboid = units
• Total surface Area of cuboid = 2( lb + bh + lh) sq units
• Lateral surface Area of cuboid = 2 (l × b)× h sq. units
• Volume of cuboid = lbh cubic units
• Area of 4 walls of room = 2 (l × b)× h sq.units
Volume and Surface Area of Cube
The cuboid whose length breath and height are equal is called a cube.
Let the edge of a cube be ‘a’ units then
• Diagonal of cube = a units
• Total surface Area of cube = 6 square units
• Lateral surface Area of cube = 4 square units
• Volume of cube = cubic units








