Algebra

1. INTRODUCTION
Our study so far has been with numbers and shapes. We have learnt numbers, operations on numbers and properties of numbers. We applied our knowledge of numbers to various problems in our life. The branch of mathematics in which we studied numbers is arithmetic. We have also learnt about figures in two and three dimensions and their properties. The branch of mathematics in which we studied shapes is Geometry. Now we begin the study of another branch of mathematics. It is called Algebra.
The main feature of the new branch which we are going to study is the use of letters. Use of letters will allow us to write rules and formulas in a general way. By using letters, we can talk about any number and not just a particular number. Secondly, letters may stand for unknown quantities. By learning methods of determining unknowns, we develop powerful tools for solving puzzles and many problems from daily life. Thirdly, since letters stand for numbers, operations can be performed on them as on numbers. This leads to the study of algebraic expressions and their properties.

2. VARIABLES
An unknown quantity can be represented by a variable. Usually, a variable is any letter from the English alphabet that represents an unknown quantity. The relation between the unknown quantity and other quantities can be expressed with the help of the variable. The value of the variable varies with the given condition on the variable. A quantity whose value does not vary is called a constant. An expression consisting of variables, constants and mathematical operators is called an algebraic expression. Mathematical operations such as addition, subtraction, multiplication and division can be easily performed on variables. We can use variables to form expressions based on patterns.
The following are some branches of mathematics:
• The branch of mathematics where letters are used along with numbers is called algebra.
• The branch of mathematics that deals with numbers, operations on numbers and properties of numbers is called arithmetic.
• The branch of mathematics that deals with the figures and shapes is called geometry.
Use of Variables
Variables are used to frame rules to find the perimeter of a polygon. The perimeter of a polygon can be obtained by adding the lengths of its sides. The following are simple rules to frame the perimeter of geometrical figures using variables.
If the length of the side is denoted by variable’s’, then the perimeter of a square is equal to 4s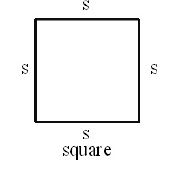

If the length and breadth of a rectangle is l, b. Then a perimeter of a of rectangle is 2(l + b)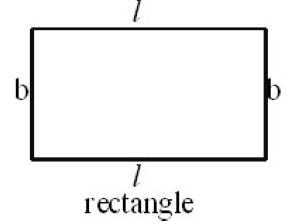

If the lengths of the sides of a triangle are denoted by x. y and z then the perimeter of the triangle is equal to x + y + z.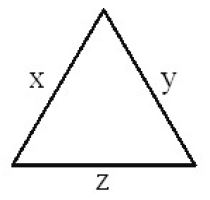

3. RULES OF ARITHMETIC
The following are some simple rules for the properties of numbers using variables.
Commutative Property of Addition: This property states that two numbers can be added in any order. If a and b represent any two numbers, then a + b = b + a
Commutative Property of Multiplication: This property states that two numbers can be multiplied in any order. If a and b represent any two numbers, then a × b = b × a
Associative Property of Addition: This property states that three numbers can be added in any order. If a, b and c represent any three numbers, then (a + b) + c = a + (b + c)
Associative Property of Multiplication: This property states that three numbers can be multiplied in any order. If a, b and c represent any three numbers, then (a × b) × c = a × (b × c)
Distributive Property of Multiplication over Addition: This property states that if a, b, and c represent any three numbers, then a × ( b + c) = a × b + a × c

4. EQUATIONS
A mathematical statement that indicates that the value of the LHS is equal to the value of the RHS is called an equation.
• An equation puts a condition on the variable.
• The value for which the equation is satisfied is the solution of the equation.
Eg: The equation $\frac{n}{3}=15$ is satisfied for n=45
• The value of the variable in an equation that satisfies the equation, or makes its LHS equal to its RHS, is the solution.
• An equation can contain numbers and variables.
Eg: a – 2 = 30, 72 ÷ 9 = 8 .
• An equation is said to be algebraic equation if it consists of a variable.
Eg: 20x = 400.
• A single variable equation will have a unique solution.
Eg: 15n = 225
• An equation that does not have any variable is called a numerical or an arithmetic equation.
Eg: 17 × 2 = 34
Different numerical values for the variable are substituted in an algebraic equation, and the solution is obtained by using a method called the trial and error method.
If there is no sign of equality between the LHS and the RHS, then it is not an equation.
Eg: $x+5>6, \frac{n}{9}>7$ are not equations.

5. ALGEBRAIC EXPRESSION
A combination of constants and variables connected by the sign of fundamental operations of addition, subtraction, multiplication and division are called algebraic expressions.
Eg: $2x^3+x^2–4x+5$
Algebraic Terms
A term in an algebraic expression is any chunk of symbols set off from the rest of the expression by either addition or subtraction.
Here are some examples:

When a term has a variable, it’s called an algebraic term. When it doesn’t have a variable, it is called a constant. For example, look at the following expression: $x^{2}y+\frac{z}{3}–xyz+8$
The first three terms are algebraic terms, and the last term is a constant. As you can see, in algebra, constant is just a fancy word for number.
Rearranging Terms
After you understand how to separate an algebraic expression into terms, you can go one step further by rearranging the terms in any order you like.
For example, suppose you begin with the expression –5x + 2. You can rearrange the two terms of this expression without changing its value. Notice that each term’s sign stays with that term, though dropping the plus sign at the beginning of an expression is customary. Rearranging terms in this way does not affect the value of the expression because addition is commutative that is, you can rearrange things that you are adding and without changing the answer.
Example: suppose x = 3. Then the original expression and its rearrangement evaluate as follows:

Rearranging expressions in this way becomes handy later in this chapter, when you simplify algebraic expressions. As another example, suppose you have this expression: 4x – y + 6
You can rearrange it in a variety of ways:
= 6 + 4x – y
= –y + 4x + 6
Because the term 4x has no sign, it is positive, so you can write in a plus sign as needed when rearranging terms.
As long as each term’s sign stays with that term, rearranging the terms in an expression has no effect on its value.
For example, suppose that x = 2 and y = 3. Here is how to evaluate the original expression and the two rearrangements:

Polynomials
An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial.
Eg: $2x^2–3x–5$ is a polynomial $\frac{1}{2}{x}^3–3x^2+5x^{\frac{1}{2}}+x–1$ is not a polynomial because it contains a term $5{\mathrm{x}}^{\frac{1}{2}}$ which contains $\frac{1}{2}$ as the power of variable x, which is not a non-negative integer.
Degree of Polynomial is one Variable
In a polynomial in one variable, the highest power of the variable is called its degree.
Eg: 2x + 3 is a polynomial in ‘x’ of degree 1
$2x^2–3x+5$ is a polynomial in ‘x’ of degree 2
$3x^4–7x^2+\frac{5}{2}x+\frac{1}{3}$ is a polynomial in ‘x’of degree 4
Degree of a Polynomial is two Variables
In a polynomial in more than one variable, the sum of the powers of the variables in each term is computed and the highest sum so obtained is called the degree of the polynomial.
Eg: $3x^4–2x^3{y}^2+7x{y}^3–9x+5y+4$ is polynomial in ‘x’ and ‘y’ of degree 5
Degree of x3y2 is 3 + 2 = 5
Constant Polynomial: A polynomial consisting of a constant term only is called a constan polynomial. The degree of a constant polynomial is zero.
Eg: 5, 7
Linear Polynomial: A polynomial of degree1 is called a linear polynomial.
Eg: $2–\frac{3}{4}\mathrm{x}, \frac{1}{2}+\frac{3}{5}\mathrm{y}, 2+3\mathrm{a}$ etc.
Quadratic Polynomials: A polynomial of degree 2 is called a quadratic polynomial
Eg: $2x^2–3x+4, 2–x+x^2$ are quadratic polynomials
Cubic Polynomials: A polynomial of degree 3 is called a cubic polynomial.
Eg: $x^3–7x^2+2x–3$
Bi Quadratic Polynomial: A polynomial of degree 4 is called bi quadratic polynomial.
Eg: $3x^4–7x^3+x^2–x+9$
A polynomial is said to be a monomial, a binomial or a trinomial accordingly as it contains one term, two terms or three terms respectively. Every polynomial is an algebraic expression but an algebraic expression need not be a polynomial.
Like Terms: Terms having the same literal factors are called like terms.
Eg: $2ab, –7ab, \frac{2}{3}ab, 9ab$