4.1 SIMILAR POLYGONS
Two polygons of the same number of series are said to be similar if
(i) Their corresponding angles are equal (i.e. they are equiangular) and
(ii) Their corresponding sides are in the same ratio (or proportion).
Example 1
In the polygons ABCD and A’B’C’D’E’
and
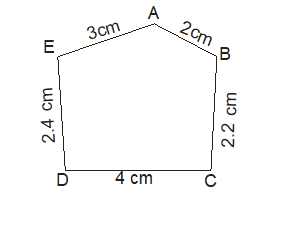
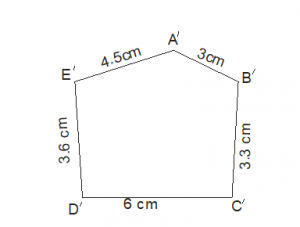
Therefore, the two polygons ABCD and A’B’C’D’E’ satisfy the conditions necessary for them to be similar. Hence, polygons ABCDE and A’B’C’D’E’ are similar. We write ABCDE ~ A’B’C’D’E’ where the symbol ~ stands for ‘is similar to’.
4.2 SIMILARITY OF TRIANGLES
Since triangles are also polygons, therefore the same conditions of similarity are applicable to them
Two triangles are said to be similar
(i) If their corresponding angles are equal and
(ii) Their corresponding sides are in the same ratio (or proportion).
Example 2
In the triangles ABC and A’B’C’
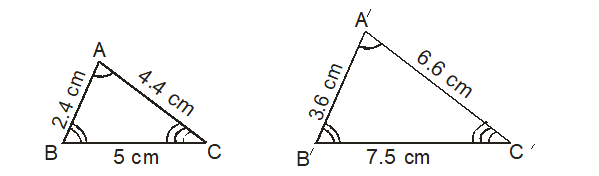
Therefore, ABC and A’B’C’ satisfy both the condition necessary for them to be similar.
Hence, ABC ~ A’B’C’
4.3 RESULT ON SIMILAR TRIANGLES
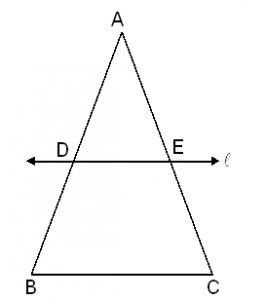
Basic Proportionality Theorem or
Thales theorem:
If a line is drawn parallel to one side of a triangle, to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
ABC in which DE || BC and DE intersects AB at D and AC at E. then:
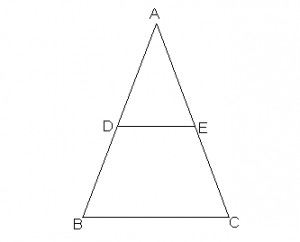
Converse of Basic Proportionality Theorem
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
There is a and a line intersecting AB at D and AC at E, such that then,
4.4 CRITERIA FOR SIMILARITY OF TWO TRIANGLES
Two triangles are said to be similar if
(i) Their corresponding angles are equal and
(ii) Their corresponds sides are in the same ratio
(or proportional).
Thus, two triangles ABC and A’B’C’ are similar if
(i)
(ii)
Characteristic Property 1 (AAA similarity)
If in two triangles, the corresponding angles are equal, then the triangles, are similar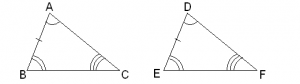
In triangles ABC and DEF and
then
Remark :
(i) Equiangular triangles are similar triangles.
(ii) Similar triangles are equiangular
Note:
If two angles of a triangle are respectively equal to two angles of another triangle then by the angle sum property of a triangle their third angle will also be equal. There AAA similarity criterion can also be stated as follows. If two angels of a triangle are respectively equal to two angles of another triangle, then the two triangles are similar. This is referred to as the AA similarity criterion for two triangles.
Characteristic Property 2 (SSS similarity)
If the corresponding sides of two triangles are proportional then they are similar.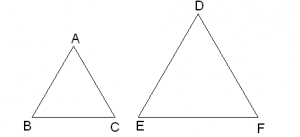
There are two triangles ABC and DEF such that
Then
Characteristic Property 3 (SAS similarity)
If one angle of a triangle is equal to the angle of the other and the sides including these angles are proportional then the two triangles are similar.
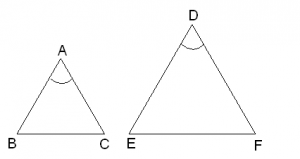
In triangle ABC and DEF
such that and
Then ABC
4.5 AREA OF SIMILAR TRIANGLES
The ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
In and , if .
Then
4.6. PYTHAGORAS THEOREM [BAUDHAYAN THEOREM]
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the right triangle, ABC right angled at B,
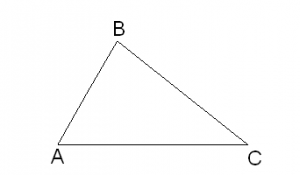
4.7. CONVERSE OF PYTHAGORAS THEOREM
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In triangle ABC if .








