Introduction to totrigonometry NCERT Questions

NCERT TEXT BOOK EXERCISES

EXERCISE-5.1

1. In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine

(i) sin A, cos A(ii) sin C, cos C

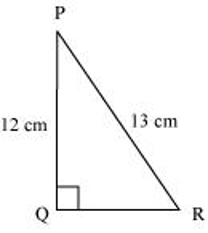
2. In the given figure find tan P − cot R

 

3. If sin A =, calculate cos A and tan A.
4. Given 15 cot A = 8. Find sin A and sec A
5. Given sec θ =, calculate all other trigonometric ratios.
6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
7. If cot θ =, evaluate

(i) (ii) cot² θ

 

8. If 3 cot A = 4, Check whether
9. In ΔABC, right angled at B. If, find the value of

(i)  sin A cos C + cos A sin C

(ii) cos A cos C − sin A sin C

10. In ΔPQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
11. State whether the following are true or false. Justify your answer.

(i)    The value of tan A is always less than 1.

(ii)   sec A =for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A

(v)   sin θ =, for some angle θ

 

EXERCISE-5.2

1. Evaluate the following

(i)    sin60° cos30° + sin30° cos 60°

(ii)   2tan²45° + cos²30° − sin²60°

(iii)

(iv)

(v)

2. Choose the correct option and justify your choice.

(i) =

(A). sin60°            (B). cos60°

(C). tan60°            (D). sin30°

(ii)

(A). tan90°            (B). 1

(C). sin45°            (D). 0

(iii) sin2A = 2sinA is true when A =

(A). 0°                  (B). 30°

C). 45°                  (D). 60°

(iv)

(A). cos60°                   (B). sin60°

(C). tan60°                    (D). sin30°

3. If and;

0° < A + B ≤ 90°, A > B find A and B.

 

4. State whether the following are true or false. Justify your answer.

(i)    sin (A + B) = sin A + sin B

(ii)   The value of sin θ increases as θ increases

(iii) The value of cos θ increases

as θ increases

(iv) sin θ = cos θ for all values of θ

(v)   cot A is not defined for A = 0°

 

EXERCISE-5.3

1. Evaluate

(I)

(II)

(III) cos 48° − sin 42°

(IV) cosec 31° − sec 59°

2. Show that

(I) tan 48° tan 23° tan 42° tan 67° = 1

(II) cos 38° cos 52° − sin 38° sin 52° = 0

3. If tan 2A = cot (A− 18°), where 2A is an acute angle, find the value of A.
4. If tan A = cot B, prove that A + B = 90°
5. If sec 4A = cosec (A− 20°), where 4A is an acute angle, find the value of A.
6. If A, Band C are interior angles of a triangle ABC then show that
7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

 

EXERCISE-5.4

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
2. Write all the other trigonometric ratios of ∠A in terms of sec A.
3. Evaluate

(i)

(ii) sin25° cos65° + cos25° sin65°

4. Choose the correct option. Justify your choice.

(i) 9 sec² A − 9 tan² A =

(A) 1         (B) 9    (C) 8    (D) 0

(ii) (1+tan θ + sec θ) (1 + cot θ − cosec θ)

(A) 0         (B) 1    (C) 2    (D) −1

(iii)  (secA + tanA) (1 − sinA) =

(A) secA               (B) sinA

(C) cosecA            (D) cosA

(iv)

(A) sec² A             (B) −1

(C) cot² A              (D) tan² A

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii)

(ix)

(x)