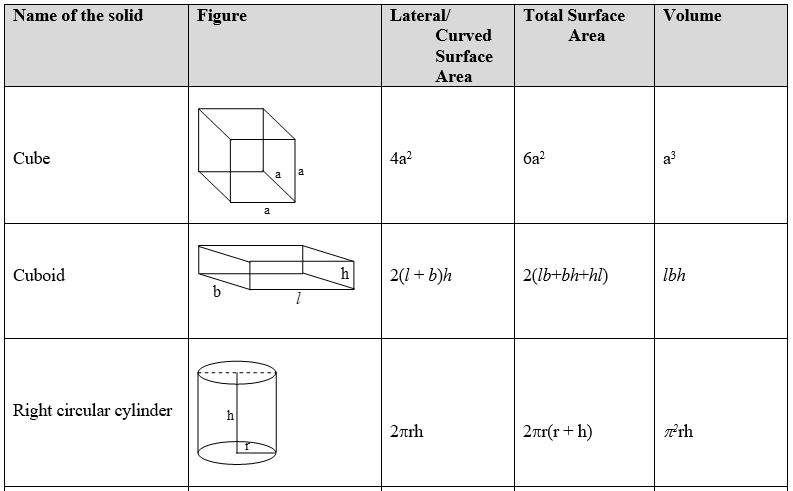
12.1. BASIC CONCEPTS
Solids
The objects having definite shape and size are called solids.
A solid occupies a definite space.
Cuboid
Solids like a matchbox, chalk box, a tile, a book, an almirah, a room, etc., are in the shape of a cuboid.
FORMULAE
For a cuboid length = l, length = b and height = h, we have
Volume = (l b h) cubic units
Total surface area = 2(lb + bh + lh) sq units
Lateral surface area = [2(l + b) h] sq units
Cube
Solids like ice cubes, sugar cubes, dice, etc., are in the shape of a cube.
FORMULAE
For cube having each edge = a unit, we have
Volume a3 cubic units
Total surface area = 6a2 sq units
Lateral surface area = 4a2 sq units
Cylinder
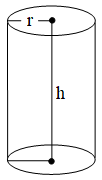
Solids like measuring jars, circular pillars, circular pencils, circular pipes, road rollers, gas cylinders etc., are said to have cylindrical shape.
FORMULAE
For a cy0linder of base radius = r and height (or length) = h, we have
Volume = (r2h) cubic units
Curved surface area = 2rh sq units
Total surface area = (2rh + 2r2) sq units
= 2r(h + r) sq units
Hollow Cylinders
Solids like iron pipes, rubber tubes are in the shape of hollow cylinders.
FORMULAE
Consider a hollow cylinder having
External radius = R, internal radius = r and height = h.
Then, we have
Volume of material
= (external volume) – (internal volume)
cubic units
cubic units
Curved surface area of hollow cylinder
= (external surface area) – (internal surface area)
Total surface area of hollow cylinder
= (curved surface area) + (area of the base ring)
Cone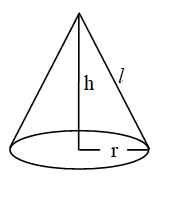
Solids like ice-cream cones, conical tents, funnels, etc, are having the shape of a cone
FORMULAE
Consider a cone in which base radius = r, height = h and slant height, .
Then, we have
Volume of the cone = cubic units
Curved surface area of the cone = sq units
Total surface area of the cone
= (curved surface area) + (area of the base)
= sq units
Sphere
Objects like a football, a cricket ball, etc., are said to have the shape of a sphere.
FORMULAE
For a sphere of radius r, we have
Volume of sphere = cubic units
Surface area of the sphere = sq units
Hemisphere
A plane through the centre of a sphere cuts it into two equal parts. Each part is called a hemisphere.
FORMULAE
For a hemisphere of radius r, we have
Volume of the hemisphere = cubic units
Curved surface area of the hemisphere = (2r2) sq units
Total surface area of the hemisphere = (3r2) sq units
12.2. SURFACE AREA OF A COMBINATION OF SOLIDS
Let us consider a container (see fig). How do we find the surface area of such a solid?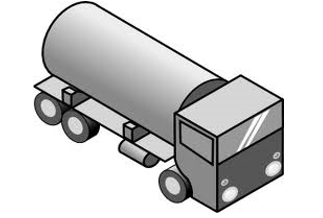
Now, whenever we come across a new problem, we first try to see, if we can break it down into smaller problems, we have earlier solved. We can see that this solid is made up of a cylinder with two hemispheres stuck at either end. It would look like what we have in the following figure after we put the pieces all together.
If we consider the surface of the newly formed object, we would be able to see only the curved surfaces of the two hemispheres and the curved surface of the cylinder. So, the total surface area of the new solid is the sum of the curved surface areas of each of the individual parts. This gives, TSA of new solid = CSA of one hemisphere + CSA of cylinder + CSA of another hemisphere where TSA, CSA stand for ‘Total Surface Area’ and ‘Curved Surface Area’ respectively.
Let us now consider another situation. Suppose we are making a toy by putting together a hemisphere and a cone. Let us see the steps that we would be going through. First, we would take a cone and a hemisphere and bring their flat faces together. Here, of course, we would take the base radius of the cone equal to the radius of the hemisphere, for the toy is to have a smooth surface. So, the steps would be as shown in below figure.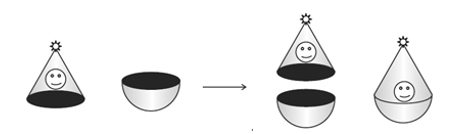
At the end of our trial, we have got ourselves a nice round-bottomed toy. Now if we want to find how much paint we would require to color the surface of this toy, what would we need to know? We would need to know the surface area of the toy, which consists of the CSA of the hemisphere and the CSA of the cone.
So, we can say: Total surface area of the toy = CSA of hemisphere + CSA of cone
12.3. VOLUME OF A COMBINATION OF SOLIDS
In the previous section, we have discussed how to find the surface area of solids made up of a combination of two basic solids. Here, we shall see how to calculate their volumes. It may be noted that in calculating the surface area, we have not added the surface areas of the two constituents, because some part of the surface area disappeared in the process of joining them. However, this will not be the case when we calculate the volume. The volume of the solid formed by joining two basic solids will actually be the sum of the volumes of the constituents, as we see in the examples below.
Example 1
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass.
Solution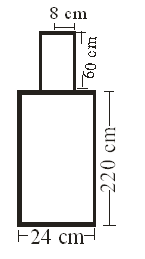
Let H be the height and R the radius of the lower cylindrical part of the iron pole.
then, H=220 cm and R=cm =12cm
Let h be the height and r the radius of the surmounted cylinder.
The volume of the iron pole =
Mass of the pole = (approx)
Hence, the mass of the pole is 892.26 kg
Example 2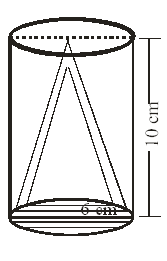
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the remaining solid.
Solution
Let r be the radius and h the height of the cylinder.
Then, r=6 cm, h=10 cm
Radius of the cone = Radius of the cylinder = 6 cm
Height of the cone = Height of the cylinder = 10 cm
Volume of the remaining solid = Volume of the cylinder – Volume of the cone
Hence, the volume of the remaining solid is
12.4. CONVERSION OF SOLID FROM ONE SHAPE TO ANOTHER
In our day to day life, sometimes we need to convert a solid into another solid into another solid of different shape or size or both, e.g. metal spheres are melted to from cylindrical metal wires, iron blocks are melted and recast into hollow cylindrical pipes, the earth taken out by digging a well is spread uniformly around the well to from an embankment in the shape of a cylindrical shell, lead pellets are made from a lead sphere etc. We shall illustrate the calculation of volumes and surface areas in such cases. Our illustrations will be based on an assumption that there is no wastage during the conversions.
Example 3
One metal solid of dimensions 16 cm × 8 cm × 5 cm and another solid of the same metal having dimensions 12 cm × 6 cm × 5 cm are melted to from a cube. Find the edge of the cube.
Solution
Let x be the side of the cube. Then, volume of the cube = x3
Volume of the cube = Volume of two rectangular solids
Hence, the edge of the cube is 10 cm.
12.5. FRUSTUM OF A CONE
If a right circular cone cut by a plane parallel to its base, through some point on its axis and the portion containing the vertex is removed, then the left out portion between the cutting plane and the base of the cone is called frustum of cone (figure. iii). thus, a function of a right circular cone has two unequal flat circular based and a curved surface, eg., flower pots, bucket, corks are generally of this shape.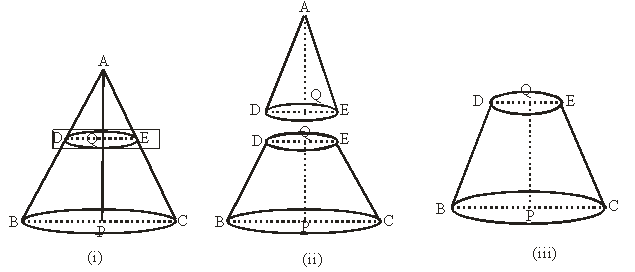
In fig. (i), let ABC represent the right circular cone which is cut by a plane DQE parallel to its circular base BPC. Solid DQECPB forms the frustum of the right circular cone ABC. The circular faces DQE and BPC are called the circular bases of the frustum. QP, the line segment joining the centers of two bases represents the perpendicular distance between the bases and is known as the height of the frustum. Each of the line segments DB and EC are called its slant height.
Volume and Surface Area of a Frustum of a Right Circular Cone
Let r1 and r2 be the radii (r1 > r2), h the right and l the slant height of frustum of a cone. Then, BP = PC r1, BD = CE = l, DQ = QE = r2 and PQ = h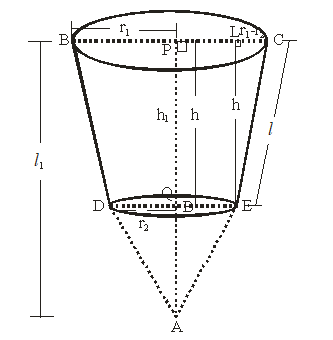
The volume of the function of the cone =
Draw ELPC. Then, LC =
In right ∆ELC, [By Pythagoras Theorem]
Curved surface area of the frustum of the cone
Hence, Curve surface area of the frustum where
Total surface area of the frustum =








