11.1. INTRODUCTION
In our daily life, we come across many circular objects like coins, cakes, plates, wheels, wheel barrows, brooches, bangles, flower beds, etc. So, the problem of finding perimeters and area of plane circular figures has great practical importance.
11.2. REVIEW OF PERIMETER AND AREA OF A CIRCLE
Circle : A circle is a closed curve consisting of a set of all those points of the plane which are at a constant distance from a fixed point in the plane.
Centre : The fixed point is called its centre.
Radius : The constant distance is called its radius. It is the line segment joining any point on the boundary (circumference) to the centre.
Circumference : The boundary (or perimeter) of a circle is called its circumference.
The circumference of a circle bears a constant ratio with its diameter. This constant ratio is denoted by Pi (), a Greek letter.
In other words,
or, Circumference = diameter =2r (where r is the radius of the circle) =2r
11.3. AREA OF CIRCLE
Cut a circle of radius r into a number of sectors and rearrange them as shown in figure.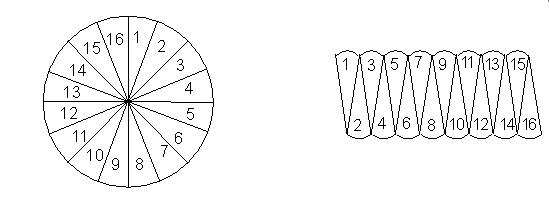
The sector can be rearranged together in nearly a rectangle of length and breadth r.
Area of the circle = area of the rectangle = length breadth =
Area of semicircle = (Area of the circle) =
Area of quadrant = (Area of the circle) =
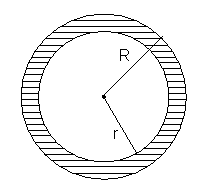
11.4. AREA ENCLOSED BETWEEN TWO CONCENTRIC CIRCLES
The fig. bounded by two concentric circles is called the annulus.
If the radii of the outer and inner circles are R and r, respectively, then Area enclosed between two concentric circles.
Some useful points about Circles
(i) If two circles touch externally, then the distance between their centres is equal to the sum of their radii (fig.)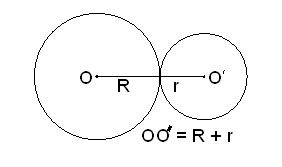
(ii) If two circles touch internally, then the distance between their centres is equal to the difference of their radii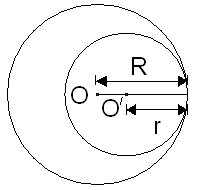
(iii) Distance covered by a moving wheel in one revolution is equal to the circumference of the wheel.
(iv) Number of revolutions made by a circular wheel = .
11.5. AREA OF SECTOR AND SEGMENT OF A CIRCLE
Sector
Recall that a sector is that portion (or part) of the circular region which is enclosed by two radii and the corresponding arc.
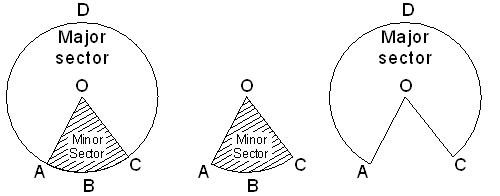
Thus, in the given fig. the shaded region OABC is a sector of the circle with centre O. it is known as minor sector because the minor arc of the circle is a part of its boundary.
AOC is called the angle of the sector.
Unshaded region OCADA is also a sector of the circle with centre O. It is known as a major sector because the major arc of the circle is a part of its boundary. the angle of the major sector OCDA is 360° – AOC.
Length of an arc of a sector
The circumference of a circular region of radius r is 2r and the degree measure of the angle subtended by it at the centre if 360.
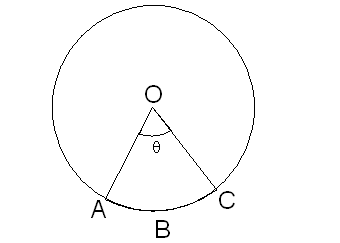
So, when the degree measure of the angel at the centre is 360, length of arc = 2r
When the degree measure of the angle at the centre is 1,
length of the arc =
When the degree measure of the angle at the centre is , the length of arc = .
Area of a Sector
Let OABC be a sector of a sector of a circle with centre O and radius r. Let the degree measure of AOC be .
Circular region can be considered as a sector forming an angle of 360°
Also, you know that the area of a circular region of radius r = r2,
So, when degree measure of the angel at the centre, is 360, area of the sector = r2.
When the degree measure of the angel at the centre is 1, area of the sector =
When the degree measure of the angel at the centre is , are of the sector
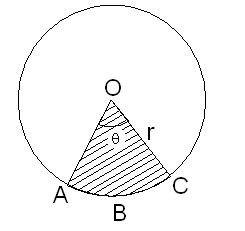
Thus, the area of the sector of angle
where r is the radius of the circle and is the angle of sector in degree.
Area of a sector =
where is the length of arc forming the boundary of the sector.
Some Useful Points about Sectors of a Circle
(i) The sum of the arcs of minor and major sectors of a circle is equal to the circumference of the circle.
i.e.
(ii) The sum of the areas of minor and major sectors of a circle is equal to the area of the circle.
i.e.
Thus, Area of the major sector of a circle of radius r = Area of the minor sector
Area of the minor sector of a circle of radius r = Area of the major sector
(iii) The angle described by a minute hand in 60 min. = 360°
So, the angle described by a minute hand in 1 minute =
Area of Segment
A segment is that portion (or part) of the circular region which is enclosed between a chord and the corresponding arc.
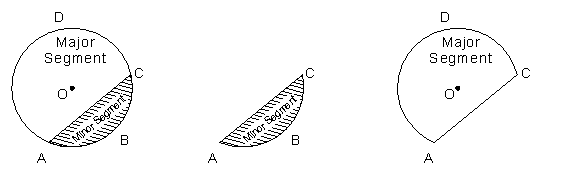
Thus, in the given figures, the shaded region ABC is a segment of the circle. It is known as a minor segment because the minor arc of the circle is a part of its boundary.
Unshaded region CDA is also a segment of the circle. It is known as a major segment because the major arc of the circle is a part of its boundary.
Area of a Segment of a Circle
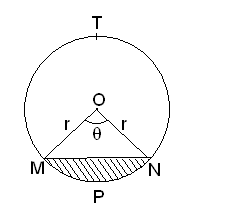
Area of the segment MPN = area of sector MPN – area of MN
If the central angle is and the radius of the circle is r then
Area of the segment MPN
=
the above expression can be written in the form
Note:
- If then OMN is an equilateral triangle, then area of segment MPN = .
- If then OMN is a right angle , then area of segment MPN = .








