13.1. INTRODUCTION
Trigonometry is one of the most ancient subjects studied by scholars all over the world. The astronomers used trigonometry to calculate distance from the Earth to the planets and stars. Trigonometry is also used in geography to construct maps, determine the position of an island in relation to the longitudes and latitudes, etc.
13.2. HEIGHTS AND DISTANCES
Let A be the top of a tower and C be the eye of a person from where he is observing the top of a tower, then AC is called the line of sight. The angle BCA, so formed by the line of sight with the horizontal level is called the angle of elevation of the top of tower from the eye of a person.
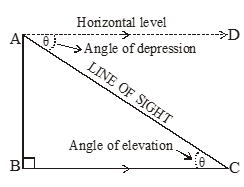
Hence, the line of sight is the line drawn from the eye of an observer to the point in the object viewed by the observer, i.e., the angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal when the point being viewed is above the horizontal level.
Let C be an object and A be the eye of a person from where he is observing the object C, then AC is called the line of sight. The angle CAD, so formed by the line of sight with the horizontal level is called the angle of depression of the object fro the eye of a person.
Hence, the line of sight is the line drawn from the eye of angle observer to the point in the object viewed by the observer, i.e., the angle so formed by the line of sight with the horizontal level is called the angle of depression. The angle of depression of a point on the object being viewed is the angle formed by the line of sight with the horizontal level when the point is below the horizontal level, i.e., the case when we lower our head to look at the point being viewed.
Now, in right ABC, we have
BC || AD and AC is a transversal.
[Altenate angles]
Hence,
Angle of elevation = Angle of depression.
Example 1
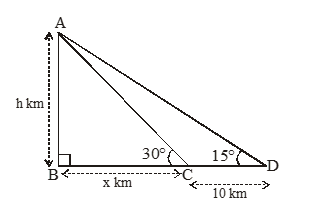
Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30 and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15.
[Use tan15 = 0.27]
Solution
Let AB be the mountain of height h km. Let C be a point at a distance of x km from the base of the mountain such that the angle of elevation of the top at C is 30. Let D be a point at a distance of 10 km from C such that the angle of elevation at D is 15 in figure.
Now, in right ABC, we have tan 30º =
… (i)
In right ,
we have = tan15=
Substituting the value of x from equation (i) in equation (ii), we get
h = (0.27) (x + 10)
h = 5
Hence, the height of the mountain (AB) = h km = 5 km.
Example 2
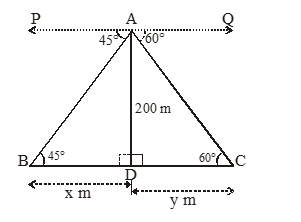
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45 and 60. Find the width of the river.
Solution
Let A be an aeroplane and AD be an altitude of 200 m. The observer observes the angles of depression of opposite points B and C on the two banks of a river as 45 and 60 respectively. Let BD = x m and Cd = y m, then we have to find the width of the river, i.e., BC = (x + y) m in figure.
Now, In right , we have tan 45º =
Again, in right we have tan 60º =
Adding (i) and (ii), we get x + y = 200 +
x + y = 315.4 m
Hence, the width of the river BC = (x + y) m = 315.4 m
Example 3
Two pillars of equal height are on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillar are 60 and 30 at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
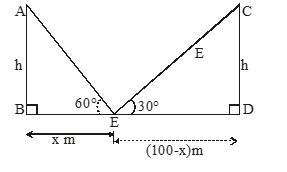
Solution
Let AB and CD be two pillars of equal height h m. Let E be a point on the road such that BE = x m. BD (width of the road) = 100 m. Then ED = (100 – x) m.
are given in the figure.
Now, In right , we have
tan60=
Again, in right CDE, we have
Substituting the value of x from equation (i) in equation (ii), we get
Again substituting the value of h in equation (i) from (iii), we get
Hence, the position of the point E from the first pillar is 25 m and 75 m from the second pillar. The height of the pillars = hm = 43.3 m
Example 4 :
A man on the top of a vertical tower observes a car having at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to charge from 30 to 45, how soon after this, will the car reach the tower? Give your answer to the nearest second.
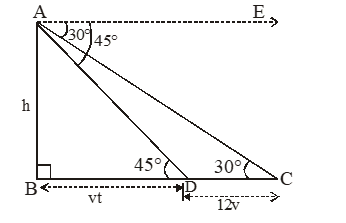
Solution
Let AB be the tower of height h m. Let C be the initial position of the car and after 12 minutes the car be at D. The angles of depression at C and D are 30 and 45 respectively. Let the speed of the car be v m/s in the figure.
Distance traveled by the car in 12 minutes = 12 v m [ distance = speed × time]
Let the car take t minutes to reach the tower AB from D. Then DB = vt m.
Now, in right , we have
Again, in right ABC, we have
Substituting the value of h from equation (i) in equation (ii), we get
Hence, the car will reach the tower from D in 16 minutes and 23 seconds.
KEY POINTS
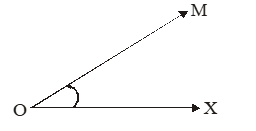
Angle of Elevation
i.e., the angle in which the line joining the object and the eye makes with the horizontal through the eye is called the angle of elevation of M as seen from O.
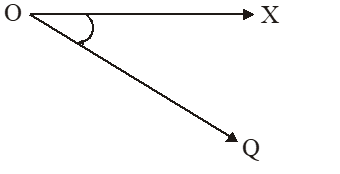
Angle of Depression
i.e., the angle in which the line joining the object and the eye makes with the horizontal through the eye is called the angle of depression of P as seen from O.
or
The angle between the horizontal line drawn through the observer’s eye and the line joining the eye to any object is called, the angle of elevation of than object when it is at joining the eye to any object is called, the angle of elevation of than object when it is at higher level than the eye.
The angle of depression of the object when it is at a lower level than the eye.
Formulae
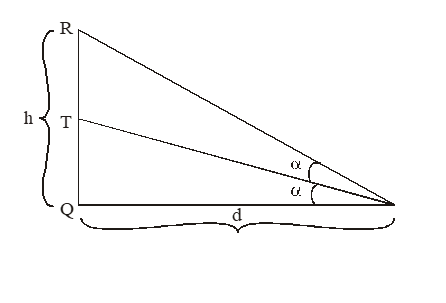
1. The angle of elevation measured from the points A, B on a horizontal line from the floor of the tower are ‘’ and ‘’ if AB = d, then the height of the tower ‘h’ is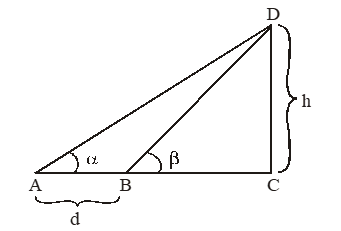
2. The angle of elevation measured from the points A, B on a horizontal line either side to the floor of the tower are ‘’ and ‘’, If AB = d. Then the height of the tower ‘h’ is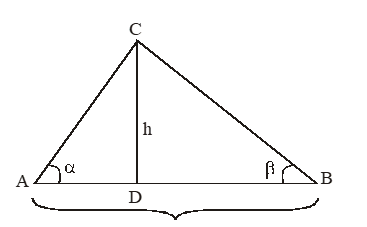
3. The angle of elevation of the top of a tower from the bottom and top of a building of height ‘d’ metres are and respectively. The height of the tower is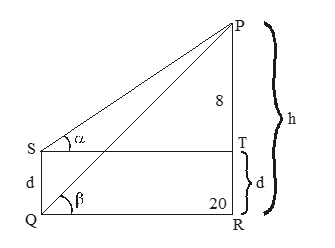
4. The angle of elevation cloud from a height ‘d’ metres above the level of water in a lake is ‘‘and the angle of depression of its image in the lake is . The height of the cloud from the water level in metres is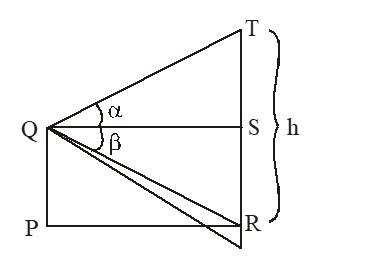
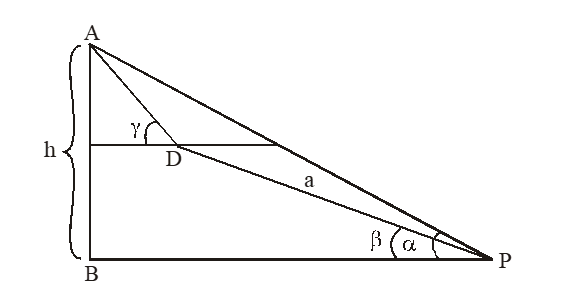
5. The angle of elevation of a hill from a point C is . After walking to some point D at a distance ‘a’ metres from C on a slope of inclination , the angle of elevation was found to be , then
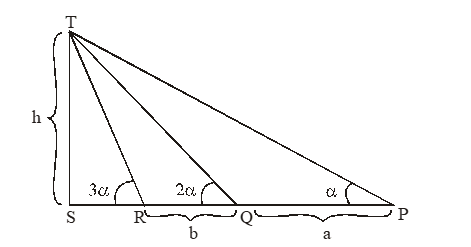
6. A balloon is observed simultaneously from the three points P, Q, R on a straight road directly beneath it. the angular elevation at Q is twice that at P and the angular elevation at ‘R’ is thrice that at P. If PQ = a and
QR = b then the height of the balloon ‘h’ in terms of a and b is,
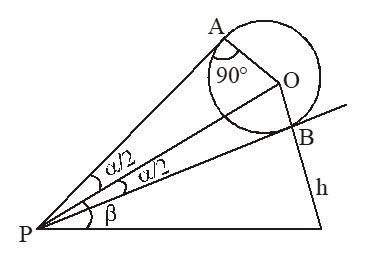
7. A round balloon of radius r subtends an angle at the eye of an observer, while the angle of elevation of its centre is . Then the height of the centre of the balloon is
8. A flag staff stands on the top of a tower of height h metres. If the tower and flag staff subtended equal angles at a distance ‘d’ metres from the foot of the tower, then the height of the flag staff in metres is