14.1. INTRODUCTION
Co-ordinate geometry helps us to locate the position of a point on a plane wherein we require a pair of co-ordinate axes. The distance of a point from the y-axis is called its X-co-ordinate, or abscissa. The distance of a point from the X-axis is called its y-co-ordinate, or ordinate. We have seen that the co-ordinates of a point on the x-axis are of the form (x, 0), and that of a point on y-axis are of the form (0, y). A linear equation in two variables, when represented graphically, produces a straight line.
Using Co-ordinate geometry we find the distance between two points whose co-ordinates are given, we can also find the co-ordinates of the point which divides the line segment joining two given points in a given ratio.
14.2. DISTANCE FORMULA
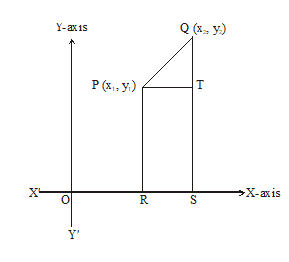
The distance between any two points in the plane is the length of the line segment joining them.
The distance between two points p(x1, y1) and Q(x2, y2) is given by
i.e., We have to find the distance between two points P(x1, y1) and Q(x2, y2). PR and QS perpendiculars have been drawn to the x-axis. A perpendicular from the point P on QS is also drawn which meets at T as shown in figure.
OR = x1 ,
OS = x2
RS = x2 – x1
PT = x2 – x1 [ RS = PT]
Again, PR = y1, QS = y2
QT = y2 – y1
Now, in right , we have
[By Pythagoras Theorem]
PQ2 =
Hence, PQ =
It is called distance formula.
The distance is always non-negative, so we take only the positive square root.
The distance of a point P(x, y) from the origin O (0,0) is given by OP=
Because the value of x1 – x2 will always be negative and its square will be positive. Similarly, the value of y1 – y2 will always be negative and its square will be positive.
Hence, there will not be any change in the value of both the formulae.
14.3. SECTION FORMULA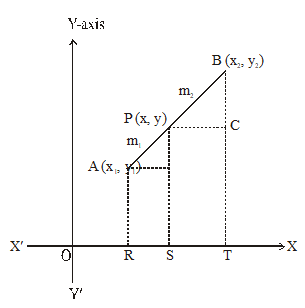
A point P divides the straight line joining two points A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2, to find the co-ordinates of P.
Let the co-ordinate of P be (x, y). AR, BT and PS perpendiculars have been drawn on the X-axis from A, B and P respectively. Now, AQ and PC perpendiculars have been drawn from A and C on PS and BT respectively. In figure.
AQ = RS = OS – OR = x – x1,
PC = ST = OT – OS = x2 – x,
PQ = SP – SQ = SP – RA = y – y1, and
BC = TB – TC = TB – SP = y2 – y.
Now, from similar triangles APQ and PCB,
we have,
Again, from similar triangles APQ and PBC, we have
Hence, the co-ordinates of point P which divide the straight line joining two points (x1, y1) and (x2, y2) internally in the ratio m1 : m2 are,
COROLLARY
Co-ordinates of the mid-point:
If P is the mid-point of AB, then it will divide AB in the ratio of 1 : 1, then co-ordinates of P are :
14.4. AREA OF A TRIANGLE
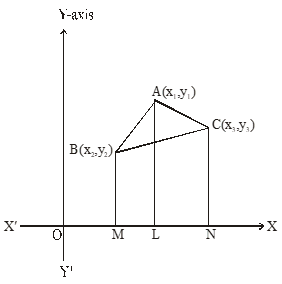
We have already studied in previous classes about how to calculate the area of a triangle when its base and corresponding height altitude are given.
We have used the formula:
Area of triangle =BaseHeight
Besides this, we have also studied in previous class about how to find the area of a triangle by using “Heron’s Formula”, When the length of the sides are given.
i.e., Area of a triangle = where s= .
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of ABC. AL , BM and CN perpendiculars have been drawn from A, B, C to the X-axis.
Area of ABC = Area of trapezium ABML + Area of trapezium ALNC – Area of trapezium BMNC
We know that:
The area of a trapezium =(sum of parallel sides)(distance b/w them)
Area of
Hence, the area ofABC








