3.1 Introduction
Linear equations in two variables are equations where we have two variables. We require two equations
to find the solution of linear equations in two variables. Let’s understand the basic concept of linear equations in two variables.
Point to Remember
To solve a linear equation in one variable, only one equation is required. To solve linear equations in two variables, two linear equations in the same two variables are required. Likewise, we can say that to solve linear equations with n number of variables, n numbers of linear equations in the same n number of variables are required.
3.2 lINEAR EQUATIONS IN TWO VARIABLES
The general form of a pair of linear equations in two variables is written as
, where , are real numbers and (i.e., )
, where , are real numbers and (i.e., )
We know that the solution of a linear equation must satisfy the equation. Conversely, we can say that the value of the variable in the equation, which satisfies the equation, is the solution of the equation.
In case of a pair of linear equations, the values of x and y, which satisfy both the equations, are the solutions of the equation.
Geometric representation of a Linear Equations
Geometrically, a linear equation represents a straight line. Every solution of an equation is a point on the line represented by the equation.
Likewise, a pair of linear equations represents two straight lines.
When their graphs are drawn, there are three possibilities.
(i) If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
(ii) If the lines coincide, then there are infinitely many solutions — each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
(iii) If the lines are parallel, then the pair of equations has no solution. In this case, the pair of equations is inconsistent.
Example 1. Find whether the given pairs of linear equations are consistent or inconsistent?
4x + y = 8
7x – 2y = 1
Solution:
4x + y = 8
7x – 2y = 1
Here, = 4 = 1 = –8
= 7 = –2 = –1
We see that
Therefore, according to the above rule, this system of equations has a unique solution.
It is represented by intersecting lines.
Example 2. There are two lines drawn in each of the following graphs. Each line represents a linear equation in two variables. State whether the pair of linear equations represented in each graph is consistent, inconsistent, or dependent.
Solution
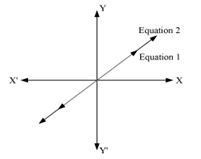
a) In the given graph, the lines representing the two equations are parallel to each other and never intersect.
Thus, the lines in this graph represent an inconsistent pair of linear equations in two variables as they do not have any solution.
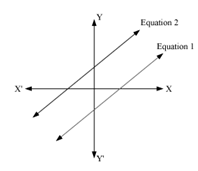
(b) In the given graph, the lines representing the two equations intersect at a point.
Thus, the lines in this graph represent a consistent pair of linear equations in two variables as they have a unique solution.
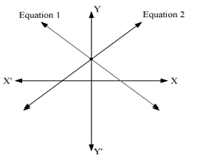
(c) In the given graph, the lines are coincident i.e., the same line represents the two equations.
Thus, the lines in this graph represent a dependent pair of linear equations in two variables as they have infinite number of solutions.
3.3 Graphical Solution Of A Pair Of Linear Equations In Two Variables
Suppose you go to a stationary shop to buy some registers and pens. If you buy two registers and two pens, then you have to pay Rs 30.
However, if you buy two registers and four pens, then you have to pay Rs 40.
Now, how can we represent this information algebraically, i.e., in the form of equations?
Let us denote the cost of each register by Rs x and that of each pen by Rs y.
Now, it is given to us that two registers and two pens cost Rs 30.
2x + 2y = 30
x + y – 15 = 0 _______________ (1)
We also know that two registers and four pens cost Rs 40.
2x + 4y = 40
x + 2y – 20 = 0 ______________ (2)
Thus, we now have two linear equations in two variables from the given situation.
x + y – 15 = 0 ______________ (1)
x + 2y – 20 = 0 ______________ (2)
These two equations are known as a pair of linear equations in two variables.
If we try to individually solve each equation, we will be unable to do so.
We can arrive at an answer only if we try and solve both these equations together.
The general form of a pair of linear equations in two variables is written as
x + y + = 0
where , , are real numbers, and
(i.e., , 0)
The lines represented by a pair of linear equations in two variables, x + y + = 0 and
x + y + = 0,
(a) have a unique solution (or are consistent) and represent intersecting lines if
(b) have infinite solutions (or are dependent) and represent coincident lines if
(c) have no solution (or are inconsistent) and represent parallel lines if
A pair of linear equations represents two straight lines.
When their graphs are drawn, there are three possibilities.
(i) The two lines may intersect at one point.
(ii) The two lines may be parallel.
(iii) They may represent the same line, i.e. they may be coincident.
The solution of a pair of linear equations is the point of intersection of their graphs.
Now, according to this, a pair of dependent equations is represented by coincident lines.
Example 3. Anshuman and Vikram have 10 marbles with them. Twice the number of marbles with Anshuman is equal to three times the number of marbles with Vikram. Solve this question graphically.
Solution : Let us suppose that Anshuman has x marbles and Vikram has y marbles.
From the given information, we can form two equations as
x + y = 10 x + y – 10 = 0 –––––––– (i)
2x = 3y 2x – 3y = 0 –––––––– (ii)
A table can be drawn for the corresponding values of x and y for equation (i) as
|
x |
y = 10 x |
|
0 |
10 0 = 10 |
|
10 |
10 10 = 0 |
Similarly, a table can be drawn for the corresponding values of x and y for equation (ii) as
|
x |
|
|
3 |
|
|
6 |
The two equations can be plotted on a graph as
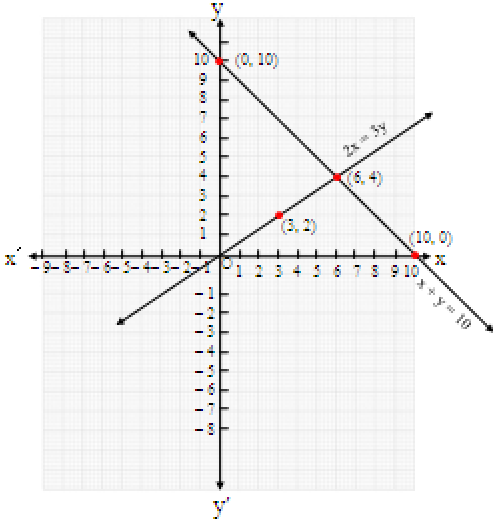
As seen in the graph, the two lines intersect at the point (6, 4).
This implies that the solution for the pair of linear equations is x = 6 and y = 4.
Thus, Anshuman has 6 marbles while Vikram has 4 marbles.
Example 4 Find graphically whether the following pairs of linear equations are consistent or inconsistent? If the equations are consistent, then find their solutions as well.
(a) 2x + 3y = 2
4x + 3y = 4
(b) x + y = 5
2x + 2y = 10
Solution
(a) 2x + 3y = 2; 4x + 3y = 4
A table can be drawn for the corresponding values of x and y for the equation 2x + 3y = 2 as
|
x |
|
|
1 |
|
|
4 |
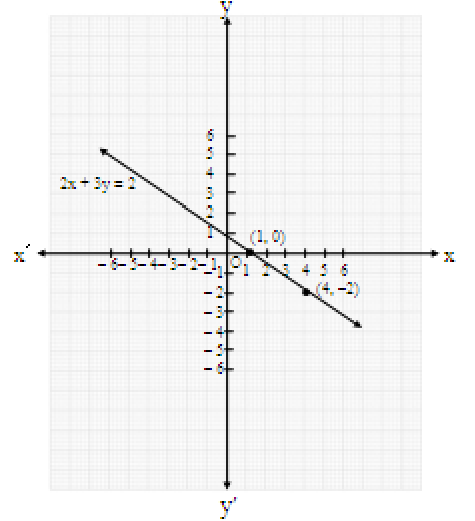
Similarly, a table can be drawn for the corresponding values of x and y for the equation 4x + 3y = 4 as
|
x |
|
|
1 |
|
These points can now be plotted and joined to obtain the graphs of the equations as
As seen in the graph, the two lines intersect at the point (1, 0).
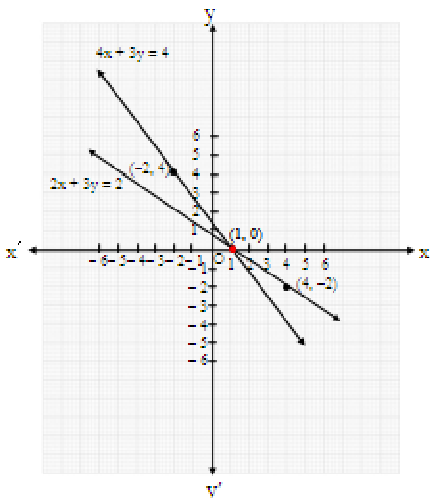
Thus, the given pair of linear equations is consistent with its solution as x = 1 and y = 0.
(b) x + y = 5 2x + 2y = 10
A table can be drawn for the corresponding values of x and y for the equation x + y = 5 as
|
x |
y = 5 |
|
0 |
|
|
10 |
Similarly, a table can be drawn for the corresponding values of x and y for the equation 2x + 2y = 10 as
|
x |
|
|
3 |
|
|
0 |
These points can now be plotted and joined to obtain the graphs of the lines as
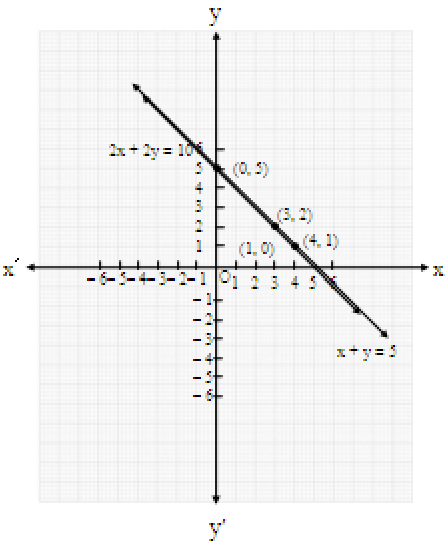
As seen in the graph, the two equations are represented by the same line.
This means that the given pair of linear equations is dependent.
Any point lying on this line is a solution to the pair of equations.
3.4 Expressing Given Situations Mathematically
We come across many situations in real life when it is easy to find the solution, if we express them mathematically.
Let us see such a situation.
The coach of the school cricket team buys 5 bats and 20 leather balls for Rs 3500.
After some time, some more boys joined the team for practice, so he buys another 4 bats and 15 balls for Rs 2750.
Suppose that the price of bat and ball does not change in the time period.
Can we express this situation mathematically to find out the individual prices of a ball and a bat?
Let the price of a bat be Rs x and that of a ball be Rs y.
It is given that 5 bats and 20 balls cost Rs 3500.
Cost of 5 bats = 5x
And cost of 20 balls = 20y
Cost of 5 bats and 20 balls = 5x + 20y
5x + 20y = 3500
Similarly, it is also given that 4 bats and 15 balls cost Rs 2750.
4x + 15y = 2750
Therefore, the algebraic representation of the given situation is
5x + 20y = 3500 _______________ (1)
4x + 15y = 2750 _______________ (2)
After solving these equations, we can find out the individual prices of the ball and the bat.
Example 5. Aman and Yash each have certain number of chocolates. Aman says to Yash, if you give me 10 of your chocolates, I will have twice the number of chocolates left with you. Yash replies, if you give me 10 of your chocolates, I will have the same number of chocolates as left with you. Write this situation mathematically?
Solution : Suppose Aman has x number of chocolates and Yash has y number of chocolates.
According to the first condition, Yash gives 10 chocolates to Aman so that Aman has twice the number of chocolates than what Yash has.
x + 10 = 2(y – 10)
x +10 = 2y – 20
x – 2y + 30 = 0 _______________ (1)
According to the second condition, Aman gives 10 chocolates to Yash such that both have equal number of chocolates.
y +10 = x – 10
Thus, the algebraic representation of the given situation is x – y – 20 = 0 __________ (2)
Example 6. Cadets in the military academy are made to stand in rows. If one cadet is extra in each row, then there would be 2 rows less. If one cadet is less in each row, then there would be 3 more rows. Express the given situation mathematically?
Solution : Let the number of cadets in each row be x and the number of rows be y.
Total number of cadets = number of rows number of cadets in each row
It is given to us that when one cadet is extra in each row, there are 2 rows less.
xy = (y – 2) (x + 1)
xy = xy – 2x + y – 2
2x – y = – 2 _________________ (1)
It is also given to us that if one cadet is less in each row, then there are 3 more rows.
xy = (y + 3) (x – 1)
xy = xy + 3x – y – 3
3x – y = 3 _______________ (2)
Thus, the algebraic representation of the given situation is
2x – y = – 2 _______________ (1)
3x – y = 3 _______________ (2)
3.5. Substitution Method Of Solving Pairs Of Linear Equations
In a class, the number of boys is 7 more than twice the number of girls.
Can you find the number of boys and girls in the class?
Let the number of boys be x and the number of girls be y.
Now, according to the given condition, x – 2y = 7
We cannot find the unique values of x and y by solving this equation because there are multiple values of x and y for which this equation holds true.
We can write the above equation as x = 2y + 7. Thus, by taking different values of y, we will obtain different values of x.
However, if we are given one more condition, then the values of x and y can be evaluated.
To solve a linear equation in two variables, two linear equations in the same two variables are required.
Let us consider one more condition.
Suppose the total number of students in the class is 52.
Now, can you find the number of boys and girls in the class?
According to this condition, we can write x + y = 52
Therefore, we obtain a pair of linear equations in two variables.
x – 2y = 7
x + y = 52
Let us solve this pair of linear equations by Substitution method.
x – 2y = 7 ____ (1)
x + y = 52 ____ (2)
y = 52 – x
substitute this value in equation (1) we get
x – 2(52 – x) = 7
x – 104 + 2x = 7
3x = 104 + 7
3x = 111
x = 37
put this value in (2) we get
y = 52 – 37
y = 15
Therefore, number of boys = 37
and number of girls = 15
In this method, we have substituted the value of one variable by expressing it in terms of the other variable to solve the pair of linear equations.
That is why this method is known as the substitution method.
Example 7. Solve the following pair of linear equations.
7x – 5y + 12 = 0
3x + 8y – 5 = 0
Solution
Given, 7x – 5y + 12 = 0 ––––––––– (i)
3x + 8y – 5 = 0 ––––––––– (ii)
From equation (i), we obtain
7x – 5y + 12 = 0
––––––––– (iii)
On substituting the value of y in equation (ii), we obtain
3.6 Elimination method to solve a pair of linear equations
There are many real life situations which can be represented in the form of linear equations.
Let us begin with such a situation.
Suppose you go to the market with your friend to buy clothes.
You buy 3 shirts and 6 pairs of jeans from a shop and the total cost of your purchase comes out to be Rs 7000.
Your friend, on the other hand buys 2 shirts and 3 pairs of jeans and the total cost of his purchase comes out to be Rs 3855.
Now, we can represent this information mathematically as pair of linear equations in two variables.
3x + 6y = 7000 ______________ (i)
2x + 3y = 3855 ______________ (ii)
We can then solve the equations and get the cost of each shirt and each pair of jeans.
Let’s solve them using the elimination method.
On multiplying equation (ii) by 2 we obtain
2(2x + 3y = 3855)
4x + 6y = 7710 ______________ (iii)
On subtracting equation (i) from (ii), we obtain
x = 7710 – 7000
x = 710
Substitute the above value in (i) we get
3 × 710 + 6y = 7000
2130 + 6y = 7000
6y = 7000 – 2130
y = 811.67
Cost of one shirt = Rs 710
Cost of 1 pair of jeans = Rs 811.67
Example 8. Solve the following equations using elimination method.
3x + 4y = 0
4x – 3y = 50
Solution
Given, 3x + 4y = 0 ______________ (i)
4x – 3y = 50 ______________ (ii)
On multiplying equation (i) by 3 and equation (ii) by 4, we obtain
9x + 12y = 0 ______________ (iii)
16x – 12y = 200 _________ (iv)
On adding equation (iii) and (iv), we obtain
25x = 200
Putting the value of x in equation (i), we obtain
3 × 8 + 4y = 0
4y = – 24
Thus, x = 8 and y = – 6.
3.7 Cross-Multiplication Method Of Solving Pairs Of Linear Equations
We can represent many situations in real life as linear equation in two variables.
Let us consider such a situation.
Suppose Samay is older than Sumit by 30 years. After 5 years, Samay will be thrice as old as Sumit.
Can we find the present ages of Samay and Sumit?
Yes, we can find the present ages.
However, before that, we have to represent this situation in the form of linear equations in two variables.
Let the present age of Samay be x years and the present age of Sumit be y years.
It is given that Samay is older than Sumit by 30 years.
Thus, according to this condition, we have
x – y = 30
After 5 years, the age of Samay will be(x + 5) years and the age of Sumit will be (y + 5) years.
However, it is given that after 5 years, Samay will be thrice as old as Sumit. Thus, we have
x + 5 = 3 (y + 5)
x + 5 = 3y + 15
x – 3y = 10
Now, we obtain the pair of linear equations as follows:
x – y = 30 ____________ (1)
x – 3y = 10 ____________ (2)
We can find the present ages of Samay and Sumit by solving the above equations for variables x and y.
We know three methods to solve a pair of linear equations.
(i) Substitution method
(ii) Elimination method
(iii) Graphical method
Now, we will follow another method to solve linear equations in two variables.
This method is known as Cross-multiplication method.
Firstly, let us discuss this method and after that we will solve the above equations for x and y.
Cross-multiplication method
If x + y + = 0, , 0 and
x + y + = 0,, 0, then
x – y = 30 ____________ (1)
x – 3y = 10 ____________ (2)
= 1, = –1, = – 30 and
= 1, = –3, = – 10
In this way, we can solve a pair of linear equations in two variables by cross-multiplication method.
We could solve these linear equations in two variables by other methods also.
But why should we use cross-multiplication method to solve linear equations?
The cross-multiplication method is easier as compared to the other methods if the coefficients of variables in the equations are large numbers or numbers that look complex.
Example 9. Solve the following pair of linear equations in two variables by cross-multiplication method.
ax + by = + and x + y = 2a
Solution : The above two equations can be written as
ax + by – ( + ) = 0 ________________ (1)
x + y – 2a = 0 ________________ (2)
From the above two equations, we obtain
= a, = b, = – ( + ) and
= 1, = 1, = – 2a
Now,
Therefore, and
x = a – b and y =
x = a – b and y = a + b
3.8 Equations Reducible To A Pair Of Linear Equations In Two Variables
Consider the following equations.
x = y ; x = 21y + 15; m + 20n = –13; etc.
We can see that the above equations are linear equations in two variables.
However, there are many equations, which do not appear to be linear equations at first glance such as
Example10.Solve the following pair of linear equations.
Solution: ––––––––––– (1)
––––––––––– (2)
From equation (1), we can write,
––––––––––– (3)
From equation (2), we can write,
–––––––––– (4)
Let
Now, equation (3) becomes
5a + b = 7 ___________ (5)
and equation (4) becomes
2a – 3b = – 4 ___________ (6)
On multiplying (5) by 3, we obtain
15a + 3b = 21 ___________ (7)
On adding equations (6) and (7), we obtain
17a = 17 a = 1
On putting the value of a in equation (5), we obtain
5 × 1 + b = 7
5 + b = 7
b = 7 – 5 = 2
Since
x = 1
and
Thus, x = 1 and
Example11. Solve the following pair of linear equations.
Solution: The given equations can be written as
––––––––––– (1)
and
––––––––––– (2)
Let
Thus, the equations become
2a + 5b = 7 _________ (3)
and, 3a + 10b = 9 _________ (4)
Now, on multiplying equation (3) by 2, we obtain
4a + 10b = 14 _____________ (5)
On subtracting equation (4) from equation (5), we obtain
a = 14 – 9
a = 5
Putting the value of a in equation (3), we obtain
10 + 5b = 7
5b = 7 – 10
Now,
On adding these two equations, we obtain
Thus,








