5.1 Introduction
Once Anil went to Paris. He saw the Eifel Tower and he wondered how high the tower is! He wanted to know the height of the tower. Is it possible?
Sunil got a lottery ticket of 2 days and 3 nights of holiday trip to London five-star accommodation. He was staying on the fourth floor of a hotel located on the bank of the river Thames. In the morning, after waking up, with a cup of coffee he was enjoying nature. From there, he is looking down at a boat lying on the other bank of the river. Then he was thinking how to measure the width of the river?
Is all the above possible?
Can you help Anil and Sunil?
Now if you can’t, definitely you will be able to with the help of this chapter – Trigonometry.
5.2 Trigonometry
What is Trigonometry ?
It is the combination of three Greek words.
Tri + gonia + metron
Three angle measurement
Thus, Trigonometry means three-angle measurement. It is an analytical study of three-angled geometrical figures in one plane.
Application of Trigonometry
The study of trigonometry is of great importance in several fields.
1. In construction of machines.
2. In finding the distance between the heavenly bodies.
3. In finding the heights of mountains, towers etc,.
4. In land survey.
5. In finding the depth of rivers and oceans.
6. In measuring the width of rivers.
Angle
Consider a ray OA . f this ray rotates about Its end point O it takes the position OB. Then we say that AOB has been generated.
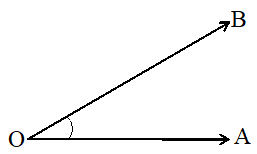
The figure obtained by two rays with same initial point is called an angle . The common initial point is called the vertex of the angle and the rays forming the angle are called it’s arms or sides. The symbol used to denote an angle is ‘’.Thus, we name the above angle as AOB or BOA. However, sometimes we may name an angle by it’s vertex alone, as O.
Example :
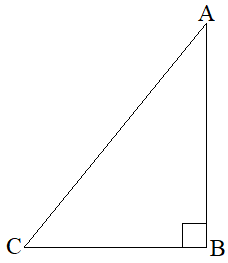
In a right-angled triangle
ABC = 90° is an angle
BAC = 60° is an angle
BCA = 30° is an angle
5.3 Different units of measuring angles
There are three known systems for measurement of angles. They are
i) Sexagesimal system (or) English system
ii) Centesimal system (or) French system
iii) Circular system (or) universally accepted system.
Sexagesimal system (or) English system
It is a system of measurement of angles in degrees.
1 right angle = 90°
Further, if one degree is divided into 60 equal parts, each part is called a minute and is written as
1 degree = 60 minutes =
Again, if one minute is further divided into 60 equal parts, each part is called a second and it is written as
1 minute = 60 seconds =
degree = 60 minutes = 3600 seconds
= 1° = =
Examples:
1. The number of minutes in 4.5 degrees
4.5° = 4.5 × 60° =
4.5 degrees = 270 minutes
2. The number of seconds in 3.2 degrees
3.2° = 3.2 × 60
=
= 192 ×
=
3.2° =
Centesimal system (or) French system
It is a system of measurement of angles in gradians.
1 right angle =
Further, if one grade is divided into 100 equal parts, each part is called one minute. It is written as
1 grade = 100 minutes =
Again, if one minute is further divided into 100 equal parts, each is part is called one second and is written as
1 minute = 100 seconds =
Examples
i) It is a system of measurement of angles in gradians.
ii) Express in sexagesimal system.
We know = 90°
Circular system
Consider a circle with centre O and radius r.
Take an arc of a circle whose length is same as the radius (r) of the circle.
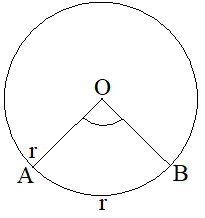
Then what is an angle subtended at its centre?
It is called a Radian.
It is written as . It is also called circular measure.
Note : Radian is not dependent on the radius of the circle. As it is accepted universally it has been used in various fields. It is called universally accepted system.
Relation between degree and radian
We know that if r is the radius of a circle, then the circumference (C) of the circle is given by 2r.
For one complete revolution,
The length of the arc = circumference of circle = 2r.
= 2r [ is the length of arc]
r = 2pr [ = r ]
= = 2 radians _________ (i)
The circumference subtends at the centre an angle whose measure is 360°.
= 360° _________ (ii)
(1) = (2) 2 radians = 360°
radians = 180°
= 57° 44.
57°
1c = 57°
1° = .
Chart of Degrees and Radians
|
S.No |
Angle in degrees |
Angle in radians |
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
Relation between degree, grade and radian
If D denotes degree, G denotes grade and C denotes radian then the relation connecting the three systems can be stated as
5.4 Trigonometric Ratios
We shall now learn the relations existing between the sides and angles of a right-angled triangle.
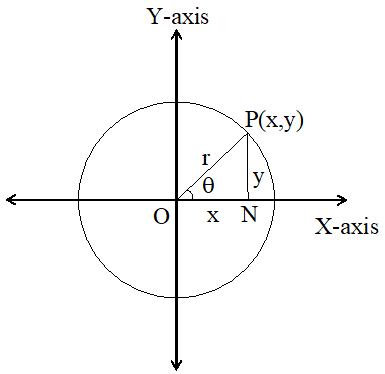
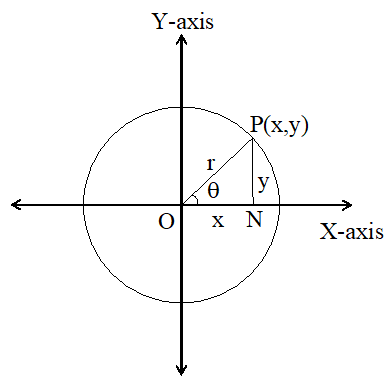
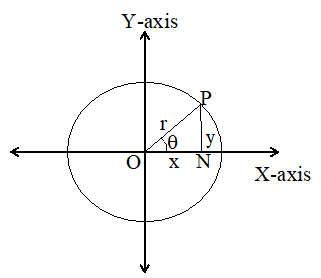
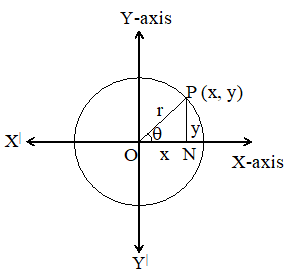
Consider a coordinate system with coordinate axes OX and OY in a plane with O as centre and r as radius and construct a circle.
Let the terminal side of an acute angle intersect the circle at P(x, y).
Draw a perpendicular PN from P to OX.
And also ON = x, NP = y and OP = r
PON = PNO = 90°
Considering ‘’ as reference,
Let us write the ratio of opposite side and hypotenuse.
The relation between the sides will form a ratio, called trigonometric ratio.
There are three sides,
With these three sides how many different ratios can we generate ?
By using three sides, there are 6 such ratios we can generate.
List of Trigonometric ratios
(i)
This ratio is called sine of angle or Sin
(ii)
This ratio is called ‘cosine’ of angle or Cos
(iii)
This ratio is called ‘tangent’ of angle or tan
(iv)
This ratio is called ‘cosecant’ of the angle or cosec
(v)
This ratio is called ‘secant’ of angle or sec
(vi)
This ratio is called ‘cotangent’ of angle cot
Reciprocal Relations of T – ratios
Let us consider a right-angled triangle ABC, right-angled at B.
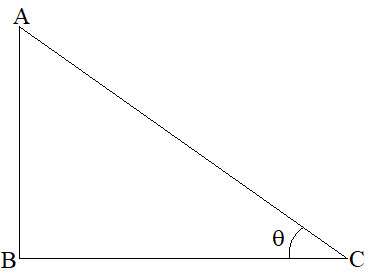
Here
sin . cosec = 1
Here the product of sin and cosec is 1.
If the product of any two quantities is 1, then they are reciprocal to each other.
Sin and cosec are reciprocal to each other.
cos and sec are reciprocal to each other.
tan . cot = 1
tan and cot are reciprocal to each other.
Summary
5.5 Trigonometric Ratios Of Different Angles
For determining the trigonometric ratios of 45°, one angle should be 45° apart from 90°.
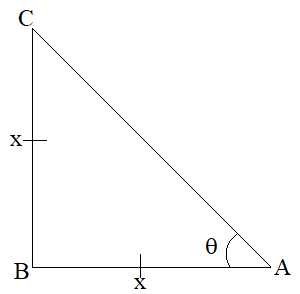
So the other angle is 45°
The triangle is right angled isosceles triangle
Now, let us consider the right-angled isosceles triangle in each equal side is considered as x units.
Then, by Pythagoras theorem,
= +
= +
= 2
Hypotenuse (AC) =
Let us consider the reference angle as A = = 45° and find the remaining angles
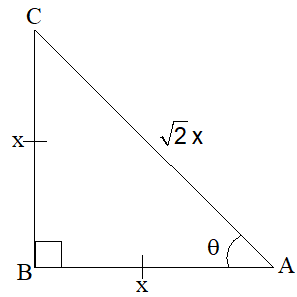
Summary
To get the trigonometric ratios of angles 30° and 60°.
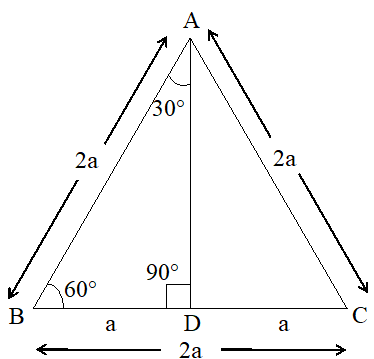
let us consider an equilateral triangle of 2a units each and split into two right-angled triangles.
In ABD the angles are 30°, 60° and 90°
= +
= +
= 4 –
= 3
In ABD : AB = 2a
BD = a
AD =
Summary
Summary
Let us decrease the angle
As the angle goes on decreasing, the opposite side(y) also decreases.
When becomes ‘0’, the opposite side ‘y’ vanishes, and the hypotenuse OP coincides with the adjacent side ON as shown below
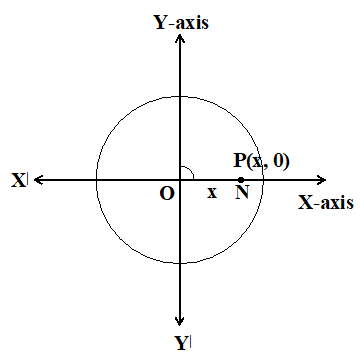
So, when = 0°, opposite side (y) = 0 and
adjacent side(x) = hypotenuse (r) = x
Summary
sin 0° = 0 cos 0° = 1 tan 0° = 0
cosec 0° = sec 0° = 1 cot 0° =
Consider a coordinate system.
Let us increase the angle
As the angle goes on increasing, the adjacent side(x) gradually decreases.
When becomes ‘90°’, the adjacent side ‘x’ vanishes and the hypotenuse OP coincides with the y-axis.
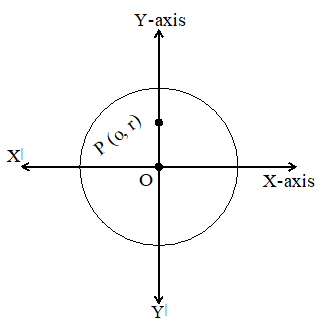
So, when = 90°, adjacent side(x) = 0
opposite side (y) = hypotenuse (r) = r
Summary
|
sine (Sin) |
0 |
1 |
|||
|
cosine (Cos) |
1 |
0 |
|||
|
Tangent |
0 |
1 |
|||
|
Cotangent |
1 |
0 |
|||
|
Secant |
1 |
2 |
|||
|
Cosecant |
2 |
1 |
Easy way to remember T – ratios
| Write the five whole numbers |
0 |
1 |
2 |
3 |
4 |
|
Divide by 4 |
|||||
|
Take the square roots |
|||||
|
Obtained values are the value of sin |
0 |
1 |
|||
|
Reverse the sin values to get the values cos |
1 |
0 |
|||
|
Divide the reciprocals of sin and cos to get he values of tan |
0 |
1 |
|||
|
Take the reciprocals of sin to get the values of cosec |
2 |
1 |
|||
|
Take the reciprocals of cos to get the values of sec |
1 |
2 |
|||
|
Take the reciprocals of tan to get the values of cot |
1 |
0 |
5.6 Trigonometric Ratios of Complementary angles
Two angles are said to be complementary when their sum is 90°.Thus, q and 90 – are complementary angles.
Example: (45 and 45), (30 and 60)
If is an acute angle, then the trigonometric ratios of complementary angles are:
i) sin (90 – ) = cos
ii) cos (90 – ) = sin
iii) tan (90 – ) = cot
iv) cot (90 – ) = tan
v) sec (90 – ) = cosec
vi) cosec (90 – ) = sec
T – ratios of complementary Angles
– Proof
i) Proof of sin (90 – ) = cos
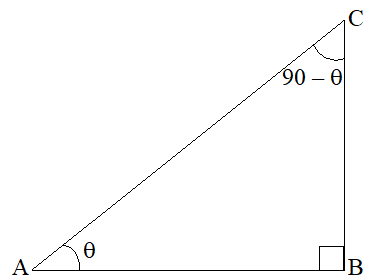
Consider a right-angled triangle ABC
A = and C = 90° –
If the concerned angle is 90 –
sin (90 – ) = cos
ii) Proof of cos (90 – ) = sin
iii) Proof of tan (90 – ) = cot
iv) Proof of cot (90 – ) = tan
cot (90 – ) tan
v) Proof of sec (90 – ) = cosec
sec (90 – ) = cosec
vi) Proof of cosec (90 – ) = sec
cosec (90 – ) = sec
Table of Complementary angles
5.7 Trigonometric Identities
An equation involving trigonometric ratios of angle q is said to be an identity if it satisfies all values of q.
Basically there are 3 identities
i) + = 1
ii) – = 1
iii) – = 1
1. Proof of + = 1
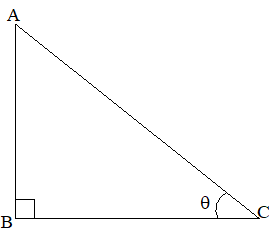
Consider a right-angled ABC, we have:
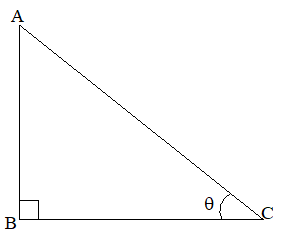
+ =
Dividing by on both the sides
+ = 1
2. Proof of – = 1
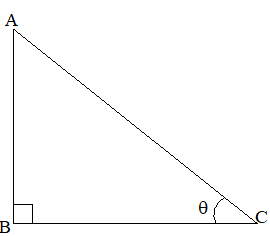
Consider a right angled D ABC,
we have:
– =
Dividing by on both the sides
3. Proof of – = 1
Consider a right angled D ABC,
we have:
– =
Dividing by on both the sides
– = 1
Compound angles of addition and subtraction
Compound Angle
It is an angle which is made up of algebraic sum or difference of two or more angles.
Addition and subtraction of compound Angles:
sin (A – B) = sin A cos B – cos A sin B
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
sin (A + B)sin(A – B) = sin2A – sin2B
Chart of Maximum and Minimum values of trigonometric ratios
|
T-ratio |
Maximum |
Minimum |
|
1 |
||
|
1 |
||








