Real Numbers - Practically Study Material

1.1 Introduction

We begin with two very important properties of positive integers , namely the Euclid’s division algorithm and the Fundamental Theorem of Arithmetic. Euclid’s division algorithm, as the name suggests, has to do with divisibility of integers. Stated simply, it says any positive integer a can be divided by another positive integer b in such a way that it leaves a remainder r that is smaller than b. Many of you probably recognise this as the usual long division process. Although this result is quite easy to state and understand, it has many applications related to the divisibility properties of integers. We touch upon a few of them, and use it mainly to compute the HCF of two positive integers.

The Fundamental Theorem of Arithmetic, on the other hand, has to do something with multiplication of positive integers. You already know that every composite number can be expressed as a product of primes in a unique way this important fact is the Fundamental Theorem of Arithmetic. Again, while it is a result that is easy to state and understand, it has some very deep and significant applications in the field of mathematics. We use the Fundamental Theorem of Arithmetic for two main applications.

First, we use it to prove the irrationality of many of the numbers , such as $\sqrt{2}$ , $\sqrt{3}$ and $\sqrt{5}$ second, we apply this theorem to explore when exactly the decimal expansion of a rational number, say $\frac{p}{q} (q \neq 0)$ is terminating and when it is nonterminating repeating. We do so by looking at the prime factorisation of the denominator $q o f \frac{p}{q}$ You will see that the prime factorisation of q will completely reveal the nature of the decimal expansion of $\frac{p}{q}$ .

1.2 Euclid’s Division Lemma

Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 $\leq$ r < b. This result was perhaps known for a long time, but was first recorded in Book VII of Euclid’s Elements. Euclid’s division algorithm is based on this lemma.

Euclid’s division algorithm is a technique to compute the Highest Common Factor (HCF) of two given positive integers. Recall that the HCF of two positive integers a and b is the largest positive integer d that divides both a and b. Let us see how the algorithm works, through an example first. Suppose we need to find the HCF of the integers 455 and 42. We start with the larger integer, that is, 455. Then we use Euclid’s lemma to get 455 = 42 × 10 + 35

Now consider the divisor 42 and the remainder 35, and apply the division lemma to get 42 = 35 × 1 + 7

Now consider the divisor 35 and the remainder 7, and apply the division lemma to get 35 = 7 × 5 + 0

Notice that the remainder has become zero, and we cannot proceed any further.

We claim that the HCF of 455 and 42 is the divisor at this stage, i.e., 7. You can easily verify this by listing all the factors of 455 and 42. Why does this method work? It works because of the following result.

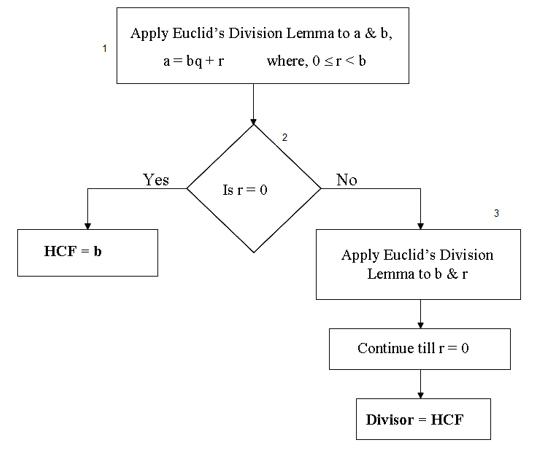
So, let us state Euclid’s division algorithm clearly.

To obtain the HCF of two positive integers, say c and d, with c > d, follow the steps below:

Step 1 : Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and r such that c = dq + r, 0 $\leq$ r < d.

Step 2 : If r = 0, d is the HCF of c and d. If r $\neq$ 0, apply >the division lemma to d and r.

Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.

This algorithm works because HCF (c, d) = HCF (d, r) where the symbol HCF (c, d) denotes the HCF of c and d, etc.

Solved Examples

Example 1 : Use Euclid’s algorithm to find the HCF of 4052 and 12576.

Solution : Step 1 : Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get

12576 = 4052 × 3 + 420

Step 2 : Since the remainder 420 0, we apply the division lemma to 4052 and 420, to get 4052 = 420 × 9 + 272

Step 3 : We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get 420 = 272 × 1 + 148

We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get 272 = 148 × 1 + 124

We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get 148 = 124 × 1 + 24

We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get 124 = 24 × 5 + 4

We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get 24 = 4 × 6 + 0

The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.

Notice that 4 = HCF (24, 4) = HCF (124, 24) = HCF (148, 124) = HCF (272, 148) = HCF (420, 272) = HCF (4052, 420) = HCF (12576, 4052).

Euclid’s division algorithm is not only useful for calculating the HCF of very large numbers, but also because it is one of the earliest examples of an algorithm that a computer had been programmed to carry out.

Remarks

1. Euclid’s division lemma and algorithm are so closely interlinked that people often call former as the division algorithm also. 2. Although Euclid’s Division Algorithm is stated for only positive integers, it can be extended for all integers except zero, i.e., b < 0. However, we shall not discuss this aspect here. Euclid’s division lemma/algorithm has several applications related to finding properties of numbers. We give some examples of these applications below:

Example 2 : Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer.

Solution : Let a be any positive integer and b = 2. Then, by Euclid’s algorithm, a = 2q + r, for some integer q 0, and r = 0 or r = 1, because 0 $\leq$ r < 2. So, a = 2q or 2q + 1.

If a is of the form 2q, then a is an even integer. Also, a positive integer can be either even or odd. Therefore, any positive odd integer is of the form 2q+1.

Example 3 : Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.

Solution : Let us start with taking a, where a is a positive odd integer. We apply the division algorithm with a and b = 4.

Since 0 $\leq$ r< 4, the possible remainders are 0, 1, 2 and 3. That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient.

However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).

Therefore, any odd integer is of the form 4q + 1 or 4q + 3.

Example 4 : A sweet seller has 420 kaju barfis and 130 badam barfis. She wants to stack them in such a way that each stack has the same number, and they take up the least area of the tray. What is the maximum number of barfis that can be placed in each stack for this purpose?

Solution : This can be done by trial and error. But to do it systematically, we find HCF (420, 130). Then this number will give the maximum number of barfis in each stack and the number of stacks will then be the least. The area of the tray that is used up will be the least. Now, let us use Euclid’s algorithm to find their HCF.

We have :

420 = 130 × 3 + 30

130 = 30 × 4 + 10

30 = 10 × 3 + 0

So, the HCF of 420 and 130 is 10.

Therefore, the sweet seller can make stacks of 10 for both kinds of barfi.

1.3 The Fundamental Theorem of Arithmetic

Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur. The Fundamental Theorem of Arithmetic says that every composite number can be factorised as a product of primes. Actually it says more. It says that given any composite number it can be factorised as a product of prime numbers in a ‘unique’ way, except for the order in which the primes occur. That is, given any composite number there is one and only one way to write it as a product of primes, as long as we are not particular about the order in which the primes occur. So, for example, we regard 2 × 3 × 5 × 7 as the same as 3 × 5 × 7 × 2, or any other possible order in which these primes are written. This fact is also stated in the following form:

The prime factorisation of a natural number is unique, except for the order of its factors.

In general, given a composite number x, we factorise it as x = $p_{1}$ $p_{2}$ … $p_{n}$ , where $p_{1}$ , $p_{2}$ ,…, $p_{n}$ are primes and written in ascending order, i.e., $p_{1}$ $\leq$ $p_{2}$ . . . $\leq$ $p_{n}$ . If we combine the same primes, we will get powers of primes.

For example ,

32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 × 32 × 5 × 7 × 13 Once we have decided that the order will be ascending, then the way the number is factorised, is unique. The Fundamental Theorem of Arithmetic has many applications, both within mathematics and in other fields. Let us look at some examples.

Solved Examples

Example 5 : Consider the numbers 4n, where n is a natural number. Check whether there is any value of n for which 4n ends with the digit zero.

Solution : If the number 4n, for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 4n would contain the prime 5. This is not possible because 4n = (2)2n; so the only prime in the factorisation of 4n is 2. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of 4n. So, there is no natural number n for which 4n ends with the digit zero.

You have already learnt how to find the HCF and LCM of two positive integers using the Fundamental Theorem of Arithmetic in earlier classes, without realising it. This method is also called the prime factorisation method. Let us recall this method through an example.

Example 6 : Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Solution : We have : $6 = 2 \times 3 = 2^{1} \times 3^{1}$ and $20 = 2 \times 2 \times 5 = 2^{2} \times 5^{1}$

You can find HCF(6, 20) = 2 and LCM(6, 20) = 2 × 2 × 3 × 5 = 60, as done in your earlier classes.

Note that HCF(6, 20) = $2^{1}$ = Product of the smallest power of each common prime factor in the numbers.

LCM (6, 20) = $2^{2}$ × $3^{1}$ × $5^{1}$ = Product of the greatest power of each prime factor, involved in the numbers.

From the example above, you might have noticed that HCF(6, 20) × LCM(6, 20) = 6 × 20. In fact, we can verify that for any two positive integers a and b,

HCF (a, b) × LCM (a, b) = a × b. We can use this result to find the LCM of two positive integers, if we have already found the HCF of the two positive integers.

Example 7 : Find the HCF of 96 and 404 by the prime factorisation method. Hence, find their LCM.

Solution : The prime factorisation of 96 and 404 gives

96 = 2 × 2 × 2 × 2 × 2 × 3 = $2^{3}$ × 3

404 = 2 × 2 × 101 = $2^{2}$ × 101

Therefore, the HCF of these two integers is $2^{2}$ = 4. Also, LCM (96, 404) = $\frac{96 \times 404}{H C F (96, 404)} = \frac{96 \times 404}{4} = 9696$

Example 8 : Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.

Solution : We have : 6 = 2 × 3, 72 = $2^{3}$ × $3^{2}$ , 120 = $2^{3}$ × 3 × 5 Here, 21 and 31 are the smallest powers of the common factors 2 and 3 respectively.

So, HCF (6, 72, 120) = $2^{1}$ × $3^{1}$ = 2 × 3 = 6

$2^{3}$ , $3^{2}$ , $5^{1}$ are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers. So, LCM (6, 72, 120) = $2^{3}$ × $3^{2}$ × $5^{1}$ = 360

Remark

Notice, 6 × 72 × 120, $\neq$ HCF (6, 72, 120) × LCM (6, 72, 120). So, the product of three numbers is not equal to the product of their HCF and LCM.

1.4 Revisiting irrational numbers

You studied about their existence and how the rationals and the irrationals together made up the real numbers. You even studied how to locate irrationals on the number line. However, we did not prove that they were irrationals. In this section, we will prove that 2 , 3, 5 and, in general, $\sqrt{p}$ is irrational, where p is a prime. One of the theorems, we use in our proof, is the Fundamental Theorem of Arithmetic. Recall, a number ‘s’ is called irrational if it cannot be written in the form $\frac{p}{q}$ where p and q are integers and $q \neq 0$ . Some examples of irrational numbers, with which you are already familiar, are : $\sqrt{2}, \sqrt{3}, \sqrt{15}, π, - \frac{\sqrt{2}}{\sqrt{3}}, 010110111011110 \dots, etc.$

Before we prove that $\sqrt{2}$ is irrational, we need the following theorem, whose proof is based on the Fundamental Theorem of Arithmetic.

Theorem : Let p be a prime number. If p divides $a^{2}$ , then p divides a, where a is a positive integer.

Proof : Let the prime factorisation of a be as follows : a = $p_{1}$ $p_{2}$ . . . $p_{n}$ , where $p_{1}$ , $p_{2}$ , . . ., $p_{n}$ are primes, not necessarily distinct. Now, we are given that p divides $a^{2}$ . Therefore, from the Fundamental Theorem of Arithmetic, it follows that p is one of the prime factors of $a^{2}$ . However, using the uniqueness part of the Fundamental Theorem of Arithmetic, we realise that the only prime factors of $a^{2}$ are $p_{1}$ , $p_{2}$ , . . ., $p_{n}$ . So p is one of $p_{1}$ , $p_{2}$ , . . ., $p_{n}$ .

Now, since a = $p_{1}$ $p_{2}$ . . . $p_{n}$ , p divides a. Therefore,

$a^{2}$ =( $p_{1}$ $p_{2}$ ,….. $p_{n}$ )( $p_{1}$ $p_{2}$ …. $p_{n}$ ) = $p_{1}^{2} p_{2}^{2} . . . . p_{n}^{2}$ .

We are now ready to give a proof that $\sqrt{2}$ is irrational. The proof is based on a technique called ‘proof by contradiction’.

Theorem : $\sqrt{2}$ is irrational.

Proof : Let us assume, to the contrary, that $\sqrt{2}$ is rational.

So, we can find integers r and s ( $\neq$ 0) such that $\sqrt{2} = \frac{r}{s}$

Suppose r and s have a common factor other than 1.

Then, we divide by the common factor to get $\sqrt{2} = \frac{a}{b}$ where a and b are coprime.

So, $b \sqrt{2} = a$

Squaring on both sides and rearranging, we get 2 $b^{2}$ = $a^{2}$ . Therefore, 2 divides $a^{2}$ .

Now, by Theorem 1.3, it follows that 2 divides a.

So, we can write a = 2c for some integer c.

Substituting for a, we get 2 $b^{2}$ = 4 $c^{2}$ , that is, $b^{2}$ = 2 $c^{2}$ .

This means that 2 divides $b^{2}$ , and so 2 divides b (again using Theorem 1.3 with p = 2).

Therefore, a and b have at least 2 as a common factor. But this contradicts the fact that a and b have no common factors other than 1.

This contradiction has arisen because of our incorrect assumption that $\sqrt{2}$ is rational.

So, we conclude that $\sqrt{2}$ is irrational.

Solved Examples

Example 9 : Prove that $\sqrt{3}$ is irrational.

Solution : Let us assume, to the contrary, that $\sqrt{3}$ is rational. That is, we can find integers a and b ( $\neq$ 0) such that $\sqrt{3} = \frac{a}{b}$ Suppose a and b have a common factor other than 1, then we can divide by the common factor, and assume that a and b are coprime. So, $b \sqrt{3} = a$

Squaring on both sides, and rearranging, we get 3 $b^{2}$ = $a^{2}$ . Therefore, $a^{2}$ is divisible by 3, and by Theorem 1.3, it follows that a is also divisible by 3.

So, we can write a = 3c for some integer c.

Substituting for a, we get 3 $b^{2}$ = 9 $c^{2}$ , that is, $b^{2}$ = 3 $c^{2}$ .

This means that b2 is divisible by 3, and so b is also divisible by 3 (using Theorem 1.3 with p = 3).

Therefore, a and b have at least 3 as a common factor. But this contradicts the fact that a and b are coprime.

This contradiction has arisen because of our incorrect assumption that $\sqrt{3}$ is rational.

So, we conclude that $\sqrt{3}$ is irrational.

Note :

• the sum or difference of a rational and an irrational number is irrational

• the product and quotient of a non-zero rational and irrational number is irrational. We prove some particular cases here.

Example 10 : Show that $5 - \sqrt{3}$ is irrational.

Solution : Let us assume, to the contrary, that $5 - \sqrt{3}$ is rational.

That is, we can find coprime a and b $(b \neq 0)$ such that $5 - \sqrt{3} = \frac{a}{b}$

Therefore, $5 - \frac{a}{b} = \sqrt{3}$

Rearranging this equation, we get $\sqrt{3} = 5 - \frac{a}{b} = \frac{5 b - a}{b}$ .

Since a and b are integers, we get $5 - \frac{a}{b}$ is rational, and

so is $\sqrt{3}$ rational.

But this contradicts the fact that $\sqrt{3}$ is irrational.

This contradiction has arisen because of our incorrect assumption that $5 - \sqrt{3}$ is rational.

So, we conclude that $5 - \sqrt{3}$ is rational.

Example 11 : Show that $3 \sqrt{2}$ is irrational.

Solution : Let us assume, to the contrary, that $3 \sqrt{2}$ is rational. That is, we can find coprime a and b $(b \neq 0)$ such that $3 \sqrt{2} = \frac{a}{b}$ . Rearranging, we get $\sqrt{2} = \frac{a}{3 b}$ .

Since 3, a and b are integers, $\frac{a}{3 b}$ is rational, and so $\sqrt{2}$ is rational.

But this contradicts the fact that $\sqrt{2}$ is rational.

1.5 Revisiting Rational Numbers and Their Decimal Expansions

We know that rational numbers have either a terminating decimal expansion or a non-terminating repeating decimal expansion. In this section, we are going to consider a rational number, say $\frac{p}{q} (q \neq 0)$ , and explore exactly when the decimal expansion of $\frac{p}{q}$ is terminating and when it is non-terminating repeating (or recurring). We do so by considering several examples.

Let us consider the following rational numbers:

(i) 0.375

(ii) 0.104

(iii) 0.0875

(iv) 23.3408.

Now,

(i) $0.375 = \frac{375}{1000} = \frac{375}{10^{3}}$

(ii) $0.104 = \frac{104}{1000} = \frac{104}{10^{3}}$

(iii) $0.0875 = \frac{875}{10000} = \frac{875}{10^{4}}$

(iv) $23.3408 = \frac{23 3408}{10000} = \frac{233408}{10^{4}}$

As one would expect, they can all be expressed as rational numbers whose denominators are powers of 10. Let us try and cancel the common factors between the numerator and denominator and see what we get :

(i) $0.375 = \frac{375}{10^{3}} = \frac{3 \times 5^{3}}{2^{3} \times 5^{3}} = \frac{3}{2^{3}}$

(ii) $0.104 = \frac{104}{10^{3}} = \frac{13 \times 2^{3}}{2^{3} \times 5^{3}} = \frac{13}{5^{3}}$

(iii) $0.0875 = \frac{875}{10^{4}} = \frac{7}{2^{4} \times 5}$

(iv) $23.3408 = \frac{233408}{10^{4}} = \frac{2^{2} \times 7 \times 521}{5^{4}}$

Do you see any pattern? It appears that, we have converted a real number whose decimal expansion terminates into a rational number of the form $\frac{p}{q}$ , $q \neq 0$ where p and q are coprime, and the prime factorisation of the denominator (that is, q) has only powers of 2, or powers of 5, or both. We should expect the denominator to look like this, since powers of 10 can only have powers of 2 and 5 as factors. Even though, we have worked only with a few examples, you can see that any real number which has a decimal expansion that terminates can be expressed as a rational number whose denominator is a power of 10. Also the only prime factors of 10 are 2 and 5. So, cancelling out the common factors between the numerator and the denominator, we find that this real number is a rational number of the form $\frac{p}{q}$ , $q \neq 0$ where the prime factorisation of q is of the form $2^{n}$ $5^{m}$ , and n, m are some non-negative integers.

Theorem : Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form $\frac{p}{q}$ , where p and q are coprime, and the prime factorisation of q is of the form $2^{n}$ $5^{m}$ , where n, m are non-negative integers.

You are probably wondering what happens the other way round in Theorem 1.5. That is, if we have a rational number of the form $\frac{p}{q}$ , and the prime factorisation of q is of the form $2^{n}$ $5^{m}$ , where n, m are non negative integers, then does $\frac{p}{q}$ have a terminating decimal expansion?

Let us see if is some obvious reason why this is true.

You will surely agree that any rational number of the form $\frac{a}{b}$ , where b is a power of 10. Let us go back to our examples above and work backwards.

$(i) \frac{3}{8} = \frac{3}{2^{3}} = \frac{3 \times 5^{3}}{2^{3} \times 5^{3}} = \frac{375}{10^{3}} = 0.375$

$(i i) \frac{13}{125} = \frac{13}{5^{3}} = \frac{13 \times 2^{3}}{2^{3} \times 5^{3}} = \frac{104}{10^{3}} = 0.104$

$(i i i) \frac{7}{80} = \frac{7}{2^{4} \times 5} = \frac{7 \times 5^{3}}{2^{4} \times 5^{4}} = \frac{875}{10^{4}} = 0.0875$

$(i v) \frac{14588}{625} = \frac{2^{2} \times 7 \times 521}{5^{4}}$

$= \frac{2^{6} \times 7 \times 521}{2^{4} \times 5^{4}} = \frac{233408}{10^{4}} = 23.3408$

So, these examples show us how we can convert a rational number of the form $\frac{p}{q}$ , where q is of the form $2^{n}$ $5^{m}$ , to an equivalent rational number of the form $\frac{a}{b}$ , where b is a power of 10. Therefore, the decimal expansion of such a rational number terminates . Let us write down our result formally.

Theorem : Let $x = \frac{p}{q}$ be a rational number, such that the prime factorisation of q is of the form $2^{n}$ $5^{m}$ , where n, m are non-negative integers. Then x has a decimal expansion which terminates. We are now ready to move on to the rational numbers whose decimal expansions are non- terminating and recurring.

Theorem : Let $x = \frac{p}{q}$ be a rational number, such that the prime factorisation of q is not of the form $2^{n}$ $5^{m}$ , where n, m are non-negative integers. Then x, has a decimal expansion which is non- terminating repeating (recurring). From the discussion above, we can conclude that the decimal expansion of every rational number is either terminating or non-terminating repeating.

1.6 Summary

In this chapter, you have studied the following points :

1. Euclid’s division lemma : Given positive integers a and b, there exist whole numbers q and r satisfying a = bq + r, 0 $\leq$ r < b.

2. Euclid’s division algorithm : This is based on Euclid’s division lemma. According to this, the HCF of any two positive integers a and b, with a > b, is obtained as follows:

Step 1 : Apply the division lemma to find q and r where a = bq + r, 0 $\leq$ r < b.

Step 2 : If r = 0, the HCF is b. If r $\neq$ 0, apply Euclid’s lemma to b and r.

Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be HCF (a, b). Also, HCF(a, b) = HCF(b, r).

3. The Fundamental Theorem of Arithmetic : Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.

4. If p is a prime and p divides a2, then p divides q, where a is a positive integer.

5. To prove that $\sqrt{2}$ , $\sqrt{3}$ are irrationals.

6. Let x be a rational number whose decimal expansion terminates. Then we can express x in the form $\frac{p}{q}$ , where p and q are coprime, and the prime factorisation of q is of the form $2^{n}$ $5^{m}$ , where n, m are non-negative integers.

7. Let $x = \frac{p}{q}$ be a rational number, such that the prime factorisation of q is not of the form $2^{n}$ $5^{m}$ , where n, m are non-negative integers. Then x has a decimal expansion which is non terminating repeating (recurring).

NOTE

You have see that

HCF (p, q, r) × LCM (p, q, r) $\neq$ p × q × r, where p, q, r are integers, However, the following results hold good for three numbers p, q and r.

$LCM (p, q, r) = \frac{p \cdot q \cdot r \cdot H C F (p, q, r)}{H C F (p, q) \cdot H C F (q, r) \cdot H C F (p, q)} HCF (p, q, r) = \frac{p . q . r . L CM (p, q, r)}{L C M (p, q) . L C M (q, r) \cdot L C M (p, q)}$

Need Help?