Constructions

10.1. INTRODUCTION
In previous classes, we have done certain constructions using a straight edge (ruler) and a compass, e.g., bisecting an angle, drawing the perpendicular bisector of a line segment, some constructions of triangles etc. and also gave their justifications. In this chapter, we shall study some more constructions by using the knowledge of the earlier constructions. You would also be expected to give the mathematical reasoning behind why such constructions work.

10.2. DIVISION OF A LINE SEGMENT
Suppose a line segment is given and you have to divide it in a given ratio, say 3 : 2. You may do it by measuring the length and then marking a point on it that divides it in the given ratio. But suppose you do not have any way of measuring it precisely, how would you find the point? We give below two ways of finding such a point.
Construction 1
To divide a line segment in a given ratio.
Given a line segment AB, we want to divide it in the ratio m : n, where both m and n are positive integers. To help you to understand it, we shall take m = 3 and n = 2.
Steps of Construction:

1. Draw any ray AX, making an acute angle with AB.
2. Locate 5 (= m + n) points A₁, A₂, A₃, A₄ and A₅ on AX so that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
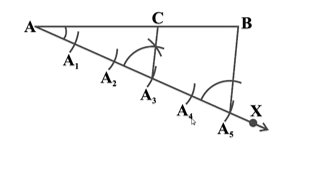
3. Join BA₅.
4. Through the point A₃ (m = 3), draw a line parallel to A₅B (by making an angle equal to $\angle$AA₅B) at A₃ intersecting AB at the point C.
   Then, AC : CB = 3 : 2.
   Let us see how this method gives us the required division.         
   Since A₃C is parallel to A₅B, therefore,
   $\frac{{\mathrm{AA}}_3}{{\mathrm{A}}_3{\mathrm{A}}_5}=\frac{\mathrm{AC}}{\mathrm{CB}}$ (By the Basic Proportionality Theorem)
   By construction, $\frac{A{A}_3}{A_3{A}_5}=\frac{3}{2}$ , Therefore $\frac{AC}{CB}=\frac{3}{2}$
   This shows that C divides AB in the ratio 3 : 2

Alternative Method
Steps of Construction

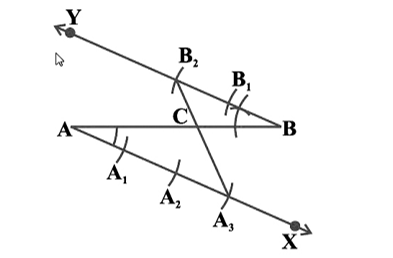
1. Draw any ray AX making an acute angle with AB.
2. Draw a ray BY parallel to AX by making $\angle$ABY equal to $\angle$BAX.
3. Locate the points A₁, A₂, A₃ (m = 3) on AX and B₁, B₂ (n = 2) on BY such that
   AA₁ = A₁A₂ = A₂A₃ = BB₁ = B₁B₂.
4. Join A₃B₂. Let it intersect AB at a point C.
   Then AC : CB = 3 : 2.         
   Why does this method work?         
   Let us see.
   Here ΔAA₃C is similar to ΔBB₂C.
   Then  $\frac{{\mathrm{AA}}_3}{{\mathrm{BB}}_2}=\frac{\mathrm{AC}}{\mathrm{BC}}$       
   Since by construction, $\frac{{\mathrm{AA}}_3}{{\mathrm{BB}}_2}=\frac{3}{2} , \mathrm{therefore}, \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{3}{2}$

In fact, the methods given above work for dividing the line segment in any ratio. We now use the idea of the construction above for constructing a triangle similar to a given triangle whose sides are in a given ratio with the corresponding sides of the given triangle.
Construction 2
To construct a triangle similar to a given triangle as per given scale factor.
This construction involves two different situations. In one, the triangle to be constructed is smaller and in the other it is larger than the given triangle. Here, the scale factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle (see also Chapter 6). Let us take the following examples for understanding the constructions involved. The same methods would apply for the general case also.

10.3. CONSTRUCTION OF TANGENTS TO A CIRCLE
Construction 3
To construct a tangent to a circle at a point P on it without using the centre of the circle.
Procedure: –

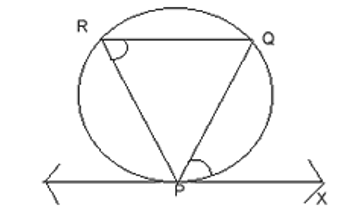
1. A chord PQ through P is drawn.
2. Any point R is taken on the major arc PQ. PR and QR are joined.
3. $\angle$QPX Equal to $\angle$PRQ is constructed.  PX is required tangent to the circle at P.

Construction 4          
To construct a tangent to circle from a point P outside the circle using its centre O.
Procedure

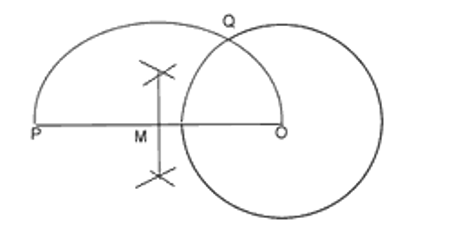
1. OP is joined and is bisected at M.
2. Taking M as centre and MO as radius a semicircle is drawn which intersect the given circle at Q.
3. PQ is the required tangent from P to the circle.

Construction 5         
To construction a tangent to a circle from a point outside the circle without using its centre.
Procedure

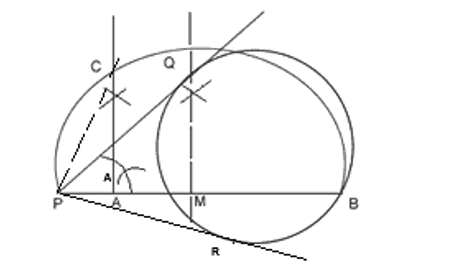
1. A secant PAB to the circle is drawn.
2. PB is bisected at M.
3. Taking M as a centre and PM as a radius, a semicircle is drawn.
4. Through A is drawn perpendicular to AB which intersect the semicircle at C.
5. Taking P as centre and PC as radius, arcs are drawn to intersect the given circle at Q and R.
6. PQ and PR are joined which is the required tangent. 

10.4. CONSTRUCTION OF INCIRCLE AND CIRCUMCIRCLE OF A TRIANGLE
Construction 6         
To construct incircle of a triangle ABC whose sides are BC = a, CA = b and AB = c.         
Procedure

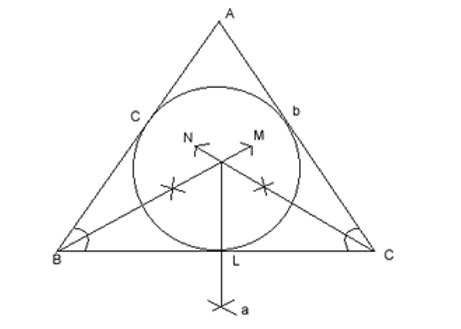
1. Triangle ABC in which BC = a, CA = b and AB = c is constructed.
2. BM and CN is constructed angle bisectors of $\angle$B and $\angle$C which intersect at I.
3. IL and BC is drawn
4. Taking I as centre and IL as radius, circle is drawn. This is the required incircle.

Construction 7         
To construct a circumcircle of a triangle ABC where a = BC, b = CA and c = AB.
Procedure

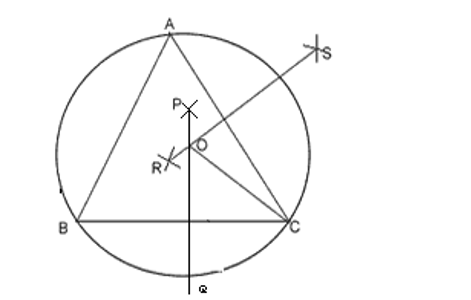
1. A triangle ABC is constructed with BC = a, CA = b and AB = c.
2. Perpendicular bisector PQ of BC and RS of CA is constructed. They intersect at O.
3. Taking O as centre and OC as a radius circle is drawn which passes through A, B and C.

10.5 CONSTRUCTION OF TRIANGLES          
Construction 8         
Construct a triangle ABC in which BC = 6cm, $\angle A=60°$ and the attitude through A is 4.5cm. Measure the length of the median through A. Write the steps of construction.
Procedure

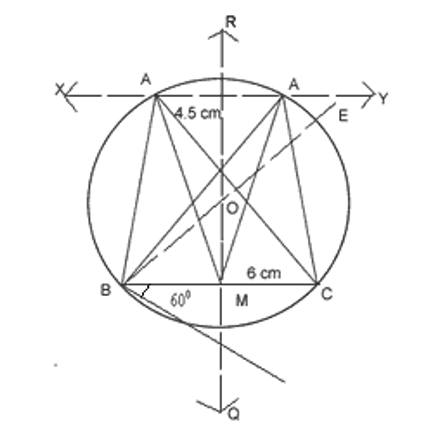
BC = 6cm is drawn and $\angle \mathrm{CBP}=60°$ is made downwards with BC of any length.

1. $\angle PBE=90°$is drawn
2. Perpendicular bisector RQ of BC is drawn which cut BC at M. and intersect BE at O.
3. Taking O as centre and OB as radius, a circle is drawn.
4. ML = 4.5cm is cut from RQ.
5. A line XY, parallel to BC is drawn through L to intersect the circle at A and A’.
   AB, AC, A’B and A’C are joined. ABC and A’BC are the required triangle
   Medium AM = A’M = 5.5cm (app.)

Construction 9 
Construct a triangle ABC in which BC = 5cm, $\angle A=70°$ and median AD through A is of length 3.5cm. Also, determine the length of the altitude drawn from A on the side BC (Write the steps of construction also).
Procedure

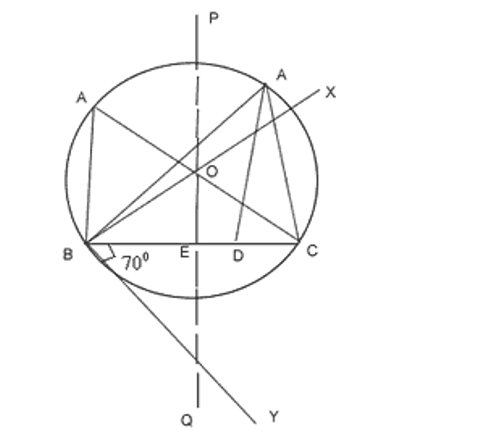
1. BC = 5cm is drawn and is constructed downwards.
2. BX is drawn perpendicular to BY.
3. Q is drawn perpendicular bisector if BC intersecting BX at O and cutting BC at E.
4. Taking O as a centre and OB as radius, a circle is drawn.
5. Taking E as centre and radius equal to 3.5cm, arc is drawn to cut the circle at A.
6. AC and AB are joined
7. AD is drawn perpendicular to BC from A to cut BC at D.
8. By measuring we find that AD = 3cm.

Construction 10
Construction a $△$ABC to a equilateral $△$PQRwith side 5cm such that each its sides is 6/7th of the corresponding side of $△$PQR  Also draw the circumcircle of $△$ABC.
Procedure

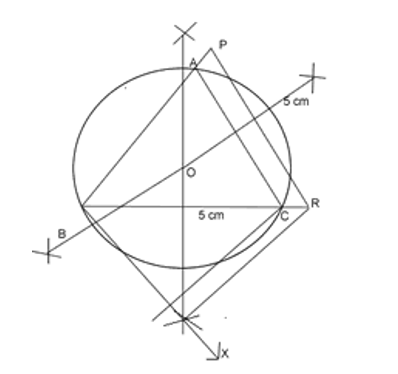
1. A ray QX is drawn making any angle with QR and opposite to P.
2. Starting from Q, seven equal line segments QQ₁, Q₁R₂, Q₂Q₃, Q₃Q₄, Q₄Q₅, Q₅Q₆, Q₆Q₇  are cut of from QX
3. RQ₇ is joined and a line CQ₆ is drawn parallel to RQ₄ to intersect QR at C.
4. Line CA is drawn parallel to PR.ABC is the required triangle.

Construction 11 
Construct a triangle ABC in which BC = 6cm, $\angle A=60°$and median AD = 5cm. Also construct another triangle BPQ similar to triangle BCA such that the side BP = 3/2BC.
Procedure

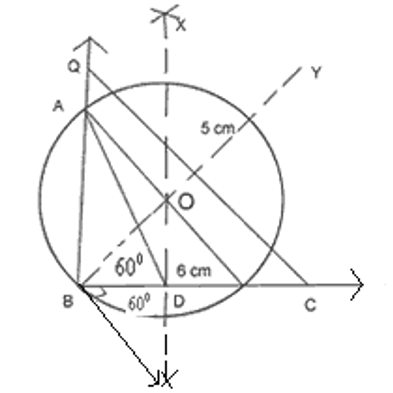
1. A line segment BC of length 6cm is drawn.
2. At B, $\angle CBX=60°$ is drawn on downwards.
3. At B, BY$\perp$BX is drawn
4. Perpendicular bisector of BC is drawn which intersect BY at O and BC at D.
5. Taking O as a center and OB as a radius a circle passing through B and C is drawn.
6. Taking D as a centre and radius 5cm an arc is drawn to intersect the circle at A.
7. AB and AC are joined. The required triangle is ABC.
8. Taking C as centre and CD as radius an arc is drawn to intersect BC produced at P such that BP = 3/2BC.
9. Through P, PQ is drawn parallel to CA meeting BA produced at Q.
10. BPQ is the required triangle similar to triangle BCA.

10.6. CONSTRUCTION OF A QUADRILATERAL         
Construction 12         
Construct a quadrilateral ABCD in which AB = 2.5cm, BC = 3.5cm, AC = 4.2cm, CD = 3.5cm and AD = 2.5cm. Construct another quadrilateral AB’C’D’ with diagonal AC’ = 6.3cm such that it is similar to quadrilateral ABCD.         
Procedure

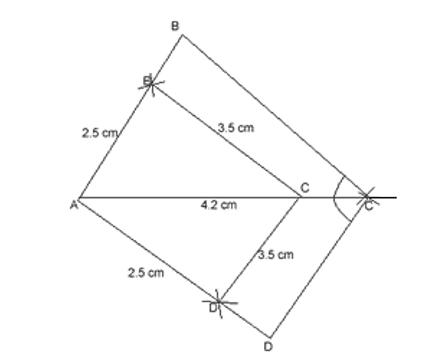
1. A line segment AC = 4.2cm is drawn.
2. With A as a centre and radius 2.5cm, two arcs, one above AC and one below AC are drawn.
3. With C as centre and radius 3.5cm, two arcs arc drawn intersecting previous arcs at B and D.
4. AB, AD, BC and CD are joined ABCD is the required quadrilateral.
5. Taking A as a centre and radius 6.3cm an arc is drawn to intersect AC produced at C’.
   Through C’, C’B’ and C’D’ are drawn parallel to CB and CD respectively. AB’C’D’ is the required quadrilateral similar to ABCD.