Circles

9.1. INTRODUCTION
Consider a circle with centre O and line AB in the same plane, then the following figure illustrate the possible relative position of the circle and the line.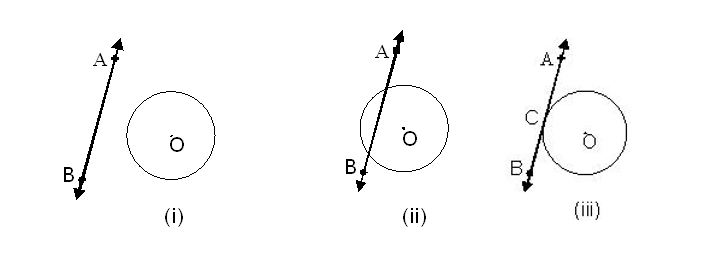

Line AB does not touch or intersect the circle.[fig. (i)]
Line AB intersects the circle in two distinct points and is called a secant (fig. (ii)) Line AB intersects the circle in two coincident points, i.e. in exactly one point (fig(iii). It is then said to touch the circle and is known as a tangent to the circle at the point. The word tangent comes from the Latin word ‘tangere’, which means to touch. This notice of touching is used in a geometrical meaning of tangent.
Hence, a tangent to a circle is a line that intersects the circle in exactly one point. The point of intersection is called the point of contact or the point of tangency. In the given figure. (iii), line AB is tangent and point C is the point of contact. A ray or line segment is a tangent if it is a part of the tangent line and contains the point of tangency (contact). Rays CA and CB are tangent rays and CA and CB are tangent segments

 9.2. NUMBER OF TANGENTS TO A CIRCLE
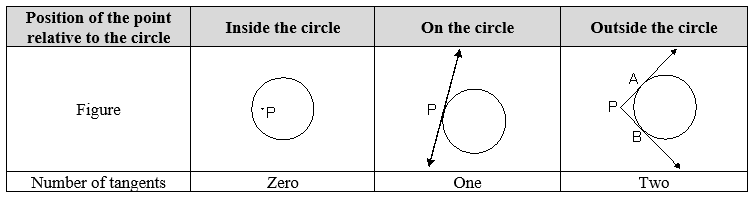
The number of tangents that can be drawn to a circle from a point depends on the position of the point relative to the circle, as shown in the following table.

 9.3. SOME RESULTS ON TANGENT TO A CIRCLE

• The tangent at any point of a circle is perpendicular to the radius through the point of contact. A circle with centre O and tangent AB at a point P.

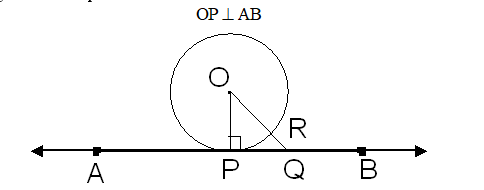
• A line drawn through the end of a radius and perpendicular to it is a tangent to the circle.

In a circle with centre O in which
(i) OP is radius
(ii) AB is line through P such that $\mathrm{OP} \perp \mathrm{AB}$ then AB is a tangent to the circle at point P.

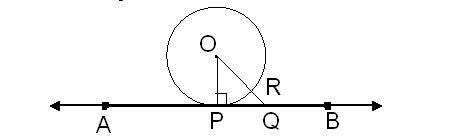
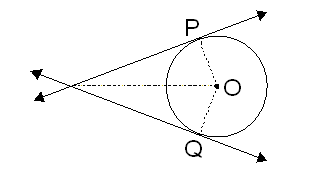
The length of tangents drawn from an external point to circle are equal.

A circle with centre O.A is an external point. Two tangents AP and AQ drawn from a point A to the circle then AP = AQ

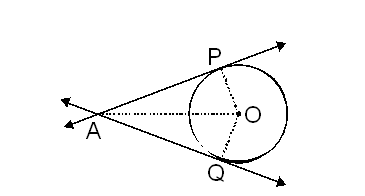
If two tangents are drawn to a circle from an external point, then

(i) They subtend equal angles at the centre
(ii) They are equally inclined to the line segment joining the centre to that point
A circle with centre O and a point A outside it. AP and AQ are tangents drawn to the circle from point A. 
$\angle \mathrm{AOP}=\angle \mathrm{AOQ} \mathrm{and} \angle \mathrm{OAP} = \angle \mathrm{AOQ}$