1.1 INTRODUCTION
The physics of motion focuses on the language, principles and laws, which describe and explain the motion of objects. The efforts should concentrate around the meaning of the information and its applications.
Mechanics is the branch of physics that focuses on the motion of objects and the forces that cause the motion to change. There are two branches of Mechanics:
Kinematics and Dynamics. The word kinematics comes from the Greek word ‘Kinema’ meaning motion. The word dynamics comes from the Greek word ‘dynamis’ meaning power. Kinematics deals with the concepts that are needed to describe motion without any reference to forces or the cause of the motion. The goal of study of kinematics is to develop sophisticated mental models which serve us in describing the motion of real world objects.
The language of kinematics deals with the words Vectors, Scalars, Distance, Displacement, Speed, Velocity, Acceleration, which are used with regularity to describe the motion of objects. Dynamics deals with the relation between the forces and motion. Scalars and Vectors Physics is a mathematical science. The underlying concepts and principles of Physics have a mathematical basis. Through the course of study of physics; the emphasis will often be upon the conceptual nature of physics, we will give considerable and persistent attention to its mathematical aspect. The motion of object can be described by words such as distance, displacement, speed, velocity and acceleration. Before we witness the concepts of kinematics, let’s review some basic concepts.
1.2 REVIEW OF BASIC CONCEPTS
Particle
An object of negligible dimensions, i.e., a point mass is known as a particle. This is only mathematical idealization. Even earth can be treated as a particle if we consider the motion of earth round the sun. The radius of the earth is very small when compared with the distance between the earth and the sun. Similarly, a bus travelling a distance of 100 km can be considered as a particle, as the size of the bus is very small compared to the distance travelled by it.
Reference point
A fixed point or a fixed object with respect to which the given body changes its position is known as reference point. For example, a pillar can be a reference point for an object crossing it.
Rest and Motion
Rest
A body is said to be at rest if it does not change its position with respect to the reference point. The objects which remain stationary at a place and do not change their position are said to be at rest.
Example : A table and the chairs lying in a room are in a state of rest, because they do not change their position with respect to the surroundings of the room. Similarly, buildings, pillars, monuments like The Taj Mahal are at rest with respect to their surroundings.
Motion
An object is said to be in motion if it changes its position from one place to another. In other words, the movement of an object is known as the motion of the object.
Examples : Cars, cycles, motorcycles, scooters, buses, rickshaws, trucks etc. running on the road. Birds flying in the sky. A lion chasing its prey. Fishes swimming in water.
Rest and Motion are relative
While sitting in a moving train, your distances from the walls, roof and the floor of the compartment do not change. That is, with respect to the compartment, your position does not change. You are at rest with respect to the compartment. But your distance from the platform, from which you boarded the train, changes as time passes. So you are apparently moving with respect to the platform. This means that an object can be at rest with respect to one thing and in motion with respect to some other thing at the same time. So motion is not
absolute; it is relative.

Is the platform at rest, or is it moving with respect to the compartment?
The distance of the platform from the compartment is changing as time passes. So the platform is moving with respect to the compartment. Also, the compartment is moving with respect to the platform.
Suppose two trains are moving on parallel tracks in the same direction. Both started together and are moving at the same speed. The distance of a person A sitting in the first train from another person B sitting in the other train will not change. So A is at rest with respect to B. Similarly, B is at rest with respect to A. Both are moving with respect to the platform, but they are at rest with respect to each other.
We are going to deal with the rectilinear motion of an object in this chapter. A broad range of physical situations are examples of straight lines or rectilinear motion:
A falling stone; an accelerating train. A braking car; A sliding hockey puck; A crate being pulled up a ramp. We describe the motion of a particle in two ways:
Mathematical equation; Graphical method. The mathematical approach is usually better for solving problems, because it permits more precision than graphical methods. The graphical method often provides more physical insight than a set of mathematical equations. In this chapter, only mathematical equations are used to describe the motion of a particle.
1.3 DISTANCE TRAVELLED AND DIS-PLACEMENT
When a body is displaced from one point to another, it describes a certain curve, which is called a trajectory of a moving body. We call the motion of a particle as rectilinear or straight line if its trajectory is a straight line.
The length of the trajectory along which a body moves for a certain time interval is said to be the path or distance traversed by the body during that time interval. The distance travelled is a physical quantity. It is measured with a special unit of length, a metre (m).
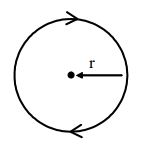
The actual length covered by a moving body in between two points, irrespective of the direction in which the body is moving, is called distance. In the figure shown, if the particle performs one complete rotation, then the distance covered by it is
The straight line distance between the initial and the final positions of a body is called the magnitude of the displacement. The direction of the displacement is given by the direction from the initial position to the final position.
The shortest distance covered by a moving body in between two points, in a particular direction, is called the displacement.
The displacement of a particle and the distance travelled by it are two different quantities. Distance travelled in a given time has just a magnitude (numerical value) and no direction, whereas the displacement has magnitude as well as direction. It is important to note that the
magnitude of the displacement is not always the same as the distance travelled. If a particle moves in a plane along a zig-zag path, the distance travelled in a given time interval may be much greater than the magnitude of its displacement in the same time interval.
Consider a particle which moves from A to B along a curve in the figure. The distance travelled is equal to the length of the curve, whereas the magnitude of the displacement is equal to the length of the straight line
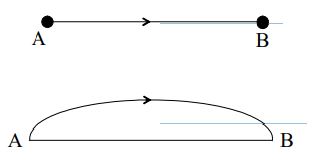
Even if the particle moves along a straight line, the distance travelled may be greater than the magnitude of its displacement. For example, if a particle goes from A to B on a straight line and returns to A, the displacement is zero but the distance traversed is not zero. Only if the particle moves along a straight line without changing its direction, the magnitude of its displacement is equal to the distance traversed as shown in above figure.
Consider the following motion depicted in the figure. A man walks 4 metres East, 2 metres South, 4 metres West and finally, 2 metres North.
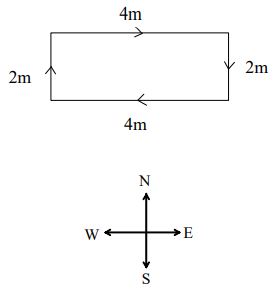
Though the man walked a total distance of 12 metres, his displacement is zero metres. During the course of this motion, he has covered 12 metres of ground (distance = 12m).
Yet when he has finished walking, he is not “ out of place” i.e., there is no displacement for his motion (displacement = 0 m). Displacement, being a vector quantity, must give attention and regard to direction. The 4 metres East is cancelled by the 4 metres West; and the 2 metres South is cancelled by the 2 metres North.
Both distance and displacement are measured in same units. In CGS and SI systems, the units are metre and centimetre, respectively.
Differences between Distance and Displacement
|
Distance |
Distance |
|
It is defined as the actual path traversed by a body. |
It is the shortest distance between two points between which the body moves. |
|
It is a scalar quantity. |
It is a vector quantity. |
|
It can never be negative or zero. |
It can be negative, zero or positive. |
|
Numerically, distance travelled by a body can be equal to or greater than displacement. |
Numerically, displacement of a body can be equal to or less than distance travelled. |
|
Distance travelled is not a unique path between two points. |
Displacement is a unique path between two points. |
|
The distance between two points gives complete information of the type of path followed by the body. |
Displacement between two points does not give complete information of the type of path followed by the body. |
|
Distance never decreases with time. For a moving body, it is never zero |
Displacement can decrease with time. For a moving body it can be zero. |
|
The S.I. unit of distance is metre and C.G.S. unit is centimetre. |
The S.I. Unit of displacement is metre and C.G.S. unit is centimetre. |
1.4 SPEED
Have you ever wondered; how the rate of motion of a body is measured? This can be understood from two terms i.e., speed and velocity. Let us first discuss about speed.
When we consider speed, we consider the total distance covered with respect to time.
Assume that a rabbit is resting at A and in search of food it moved along path ABCDEF and reached F.
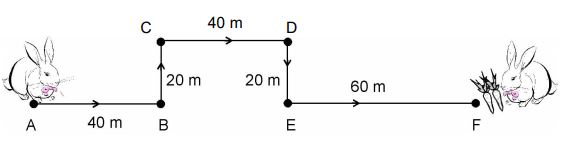
If the rabbit takes 2 minutes to reach F from A, then we say that speed of the rabbit is 1.5 m/s
Let us see how we get this
Total distance covered = 40 + 20 + 40 + 20 + 60 = 180 m
Total time taken = 2 minutes = 120 s
Thus, speed can be defined as the distance covered by a body in unit time and is represented with v.
Units: In CGS system, the unit of speed is centimetre per second (cm/s) whereas in SI system, it is metre per second (m/s).
Note:
i) Speed is a scalar quantity as it has only magnitude without any specific direction.
ii) If the distances covered are very small, then the speed is expressed in cm/s or .
iii) If the distances covered are fairly large, the speed is expressed in km/h or .
iv) 1km per hour metre per second
Uniform Speed
Observe the motion of the car shown below:
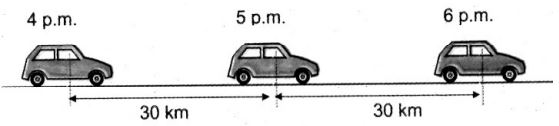
What do you observe?
The car covers 30 km in every hour. Then, we say that the car is moving with a uniform speed. When a body covers equal distances in equal intervals of time (however small the time intervals may be), the car is said to be moving with a uniform speed.
Examples:
A rotating fan, a rocket moving in space, etc., have uniform speeds. Similarly, an aeroplane flying at 200 km/h or a train running at 90 km/h are moving with uniform speeds.
Non-Uniform Speed
Let us understand the same by observing the motion of the following car.
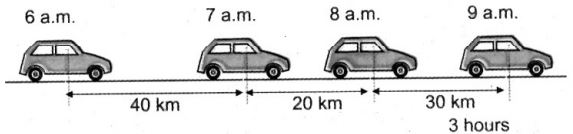
What do you observe?
We observe that the car covers 40 km from 6 a.m. to 7 a.m., 20 km from 7 a.m. to 8 a.m. and 30 km from 8 a.m. to 9 a.m. Here, the distance covered by the body is not same in equal intervals of time, or equal distances in unequal intervals of time. In such cases, we say that the body is moving with non-uniform speed or variable speed or variable speed.
When a body covers unequal distances in equal intervals of time, the body is said to be moving with a non-uniform speed.
Examples:
A train starting from a station, a dog chasing a cat, have variable speeds.
Average Speed
Let us consider the motion of the car in the previous case. The car is covering unequal distances in equal intervals of time.
How do you calculate the speed of the car for the whole journey?
In such cases, we consider the average speed of the car. Average speed of a body is the total distance covered by it in total time.
Average speed =
In the previous case, the total distance covered is (40 + 20 + 30) km = 90 km, whereas the total time taken is 3 hours.
1.5 VELOCITY
The speed of an object tells us how fast the object is moving. If the speed is known, one can calculate the distance traversed by the object in a given time interval. But to locate the position of the object at the end of the given interval of him, one needs to know the direction
in which the body has moved. Suppose, I tell you that at 10.30 a.m. a ball was placed at the centre of a field. A boy pushed the ball along the ground to move it with a uniform speed of 0.5 m/s.
Can you find the location of the ball after 1 minute?
You can only calculate the distance covered by the ball in 1 minute.
S = vt = (0.5 m/s) (60 s) = 30 m
The ball is 30 m away from the centre of the field. But this does not tell us where exactly the ball is, i.e., 30 m from the centre in which direction? To locate the position of the ball, you need to know the direction in which the ball moved with a speed of 0.5 m/s. If we say that the boy pushed the ball towards the North, it means the ball moved with a speed 0.5 m/s towards North. You can then locate the ball at a point 30 m North from the centre of the field.
When speed and direction are both specified, we get the velocity of the object. In the above example, we say that the velocity of the ball is 0.5 m/s, North. This is equivalent to the statement the speed of the ball is 0.5 m/s, and it is moving towards the North.
The velocity of an object is a quantity that gives the speed of the object as well as its direction of motion. Velocity has magnitude as well as direction. It is a vector quantity.
We can also define velocity as follows:
The velocity of an object is the displacement of the object in a short time interval divided by the time interval or the velocity of an object is its displacement per unit time.
The unit of velocity is the same as that of speed. Thus the SI unit of velocity is metre per second, written as m/s. We often use the unit km/h for convenience.
Velocity of an object moving along a straight Line
When an object moves along a straight line, there are only two possible directions of motion. In such a case, its velocity may be represented in a very simple manner. We write the speed of the object, and put a plus sign before it if the object is moving in the positive direction of the line, and a minus sign if it is moving in the negative direction of the line. The resulting number gives the speed as well as the direction of the motion, and, hence, represents velocity.
Some noteworthy points
1. Velocity is a vector quantity while speed is a scalar quantity, both having same units(m/s).
2. If during motion, velocity remains constant throughout a given interval of time, the motion is said to be uniform.
3. If velocity is constant, speed will also be constant. However, the converse may or may not be true, i.e., if speed is constant, velocity may or may not be constant as velocity has direction in addition to magnitude which may or may not change, as in the case of uniform circular motion.
4. Velocity can be positive or negative, as it is a vector; but speed can never be negative, as it is magnitude of velocity.
Uniform Velocity
When a body has equal displacements in equal intervals of time in a specified direction, (howsoever, short the time intervals may be) the body is said to be moving with a uniform velocity.
Example: Imagine a car is moving along a straight road towards East, such that in every one second it has a displacement of 5m.
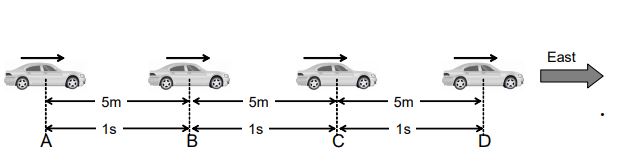
In such a case, the uniform velocity of the car is 5 m/s East as illustrated above
A body will have a uniform velocity only if :
i) It has displaces equal distances covers equal distances in equal intervals of time, i.e., the
magnitude does not change.
ii) Its direction remains the same. If any of the two conditions are not fulfilled, then the
body will have uniform velocity, but have a variable velocity.
Variable Velocity
When a body covers unequal distances in equal intervals of time in a specified direction or equal distances in equal intervals of time, but its direction changes, then the body is said to be moving with a variable velocity.
Example : A car moving along a circular path, such that it covers 5 m in every one second, as shown below.
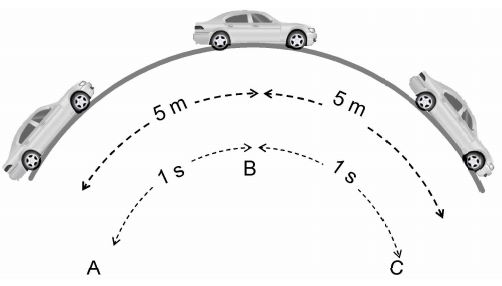
Certainly, the car has a uniform speed of 5m/s, but its uniform velocity is not 5 m/s, because the direction of the car is changing continuously
Average Velocity
It is the ratio of total displacement to total time taken.
Example :
The motion of a body along a straight line is shown below. It covers different distances in each second.
The total displacement (total distance travelled) of a body towards East is (3m + 4m + 2m + 4m) = 13m. in 4s.
Some noteworthy points
1. Average speed is a scalar while average velocity is a vector, both having same units (m/s).
2. Average speed or velocity depends on time interval over which it is defined.
3. For a given time interval average velocity is single valued while average speed can have many values depending on path followed.
4. If after motion, the body comes back to its initial position, then average velocity is zero and average speed is greater than zero and finite.
5. For a moving body average speed can never be negative or zero (unless t = ) while average velocity can be zero or negative or positive.
6. In general, average speed is not equal to magnitude of average velocity. However, it can be so if the motion is along a straight line without change in direction.
Differences between Speed and Velocity
|
Speed |
Velocity |
|
Distance travelled by a body per unit time is known as its speed. |
The distance travelled by a body in a particular direction (i.e., displacement) per unit time is known as its velocity |
|
Average speed of a moving body cannot be zero |
Average velocity of a moving body can be zero. |
|
Speed tells how fast a body moves. |
Velocity tells how fast a body moves and in which direction it moves. |
|
Speed is a scalar quantity. |
Velocity is a vector quantity. |
|
Speed of a body is always positive. |
Velocity of a body can be positive or negative. |
1.6 ACCELERATION
To develop the idea of acceleration, let us consider a body moving in a straight line with a non-uniform velocity. For example, let a train start from rest at station A. When it starts moving, its velocity increases and after a certain time interval it attains a constant velocity. As the next station approaches, its velocity gradually decreases and finally becomes zero at the station B. This can be illustrated as follows.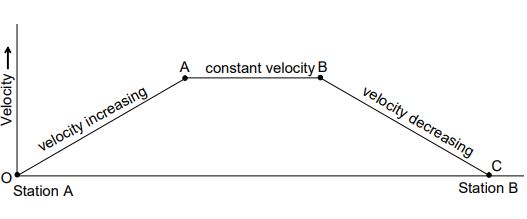
These changes in the velocity of a moving body are described in terms of acceleration. Acceleration is denoted by a, and is defined as follows:
The change in the velocity of a body per unit time is called acceleration.
If Velocity of a body at and Velocity of a body at
Then, Change in velocity = and Time interval =
As per definition, the acceleration of the body over the time interval is given by
The acceleration given by the above equation is actually the average acceleration over the time interval .
However, if the time interval ( ) is very small, then acceleration obtained is called acceleration at time .
The rate of change of velocity of a body is called its acceleration. The change in the velocity may be due to a change in its speed or direction of motion or both.
But when a body moves in a straight line, its direction does not change. So, for bodies travelling along a straight line, the acceleration is due to the change in its speed during its motion. However, when a body moves along a circular path at a constant speed, the acceleration in the body is due to the change in its direction.
Acceleration of a body in terms of its initial and final velocities
Where :
u = Initial velocity of the body
v = Final velocity of the body
t = Time interval
a = Acceleration of the body
Units of acceleration
The C.G..S and S.I units of acceleration are respectively. At times it is also measured in
Positive Acceleration
Acceleration is described by the equation,
Acceleration,
If the final velocity of a moving body is greater than the initial velocity, i.e., v > u,
then
Thus, the acceleration of a moving body is positive if its final velocity is greater than the initial velocity. In other words, when the velocity of a body increases with time, its acceleration is positive. In common parlance, positive acceleration is simply called acceleration.
Example: A body dropped from a certain height gains velocity as it falls down towards the earth. So, a body falling towards the earth has positive acceleration.
Note: Acceleration is taken to be positive if it acts in the direction of velocity, and negative when in the direction opposite to the direction of velocity.
Negative Acceleration (or Retardation)
We know,
If the final velocity of a moving body is less than the initial velocity , i.e., v < u,
then
Thus, the acceleration of a moving body is negative when its final velocity is less than the initial velocity. In other words, when the velocity of a body decreases with time, its acceleration is negative.
Example: When a ball (or stone) is thrown vertically upwards, its velocity decreases with time. So, the acceleration of a ball thrown vertically upwards is negative.
The velocity of a ball rolling on the floor keeps on decreasing until it stops. So, the acceleration of a ball rolling on the floor is also negative.
Negative acceleration is also called deceleration or retardation.
So, when the velocity of a body decreases with time, it is said to be under retardation.
For a body undergoing retardation, the final velocity is less than initial velocity. Thus, retardation is actually acceleration with a negative sign. For example, if a body has an acceleration of – 5 , then the retardation of the body is +5
Units of Retardation
Retardation (or negative acceleration) has the same units as acceleration. Thus, the SI unit of retardation is metre per second squared ()
What is meant by Uniform Acceleration?
When a moving body has the same acceleration throughout its motion, it is said to have uniform acceleration. The uniform acceleration is also called constant acceleration.
When a body travels in a straight line and its velocity changes by equal amounts in equal intervals of time, it is said to have a uniform acceleration.
The motion of a body with uniform acceleration is called uniformly accelerated motion.
Examples:
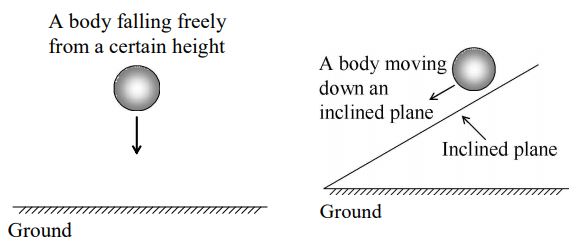
a) A body falling freely under gravity has uniform acceleration.
b) A ball moving down an inclined plane has uniform acceleration.
Non-uniform Acceleration
Non-uniform acceleration is also called variable acceleration. When a moving body has different accelerations at different points of time during its motion, it is said to have non-uniform acceleration, or variable acceleration. Acceleration is defined as the rate of change of velocity. So, the non-uniform acceleration may be defined as follows:
When the velocity of a body changes by unequal amounts in equal intervals of time, it is said to have a non-uniform acceleration.
Example. An auto/car driven on a crowded city-road with frequent applications of brakes has a non-uniform acceleration.
1.7 THE EQUATION OF MOTION
There are a variety of quantities associated with the motion of objects, displacement (and distance), velocity (and speed), acceleration, and time. Knowledge of each of these quantities provides descriptive information about an object’s motion. The equations of motion or kinematics are a set of equations which can be utilized to determine unknown information about an object’s motion if other information is known. The equations can be utilized for any motion, which can be described as being either a constant velocity motion (an acceleration of 0 ) or a constant acceleration motion. They can never be used over any time period during which the acceleration is changing. Each of the kinematics equations includes four variables; if the values of three of the four variables are known, then the value of the fourth variable can be calculated. In this manner, the kinematics equations provide a useful means
of predicting information of an object’s motion if other information is known.
For example, if the initial and final velocity of a skidding car is known, (and acceleration) then the displacement of the car and the time can be predicted using the equations of kinematics.
The equations of kinematics which describe an object’s motion, are:
Where u = initial velocity
v = final velocity
a = acceleration
s = displacement or distance covered
n or t = time in seconds
|
Note: i) If a body starts from rest, its initial velocity, u = 0 ii) If a body comes to rest (it stops), its final velocity, v = 0 iii) If a body moves with uniform velocity, its acceleration, a = 0 |
Derivations of Equations of Motion
1.
This equation gives the velocity acquired by a body in time t.
Consider a body having initial velocity u. Suppose it is subjected to a uniform acceleration a so that after time t its final velocity becomes v. Now, from the definition of acceleration we know that:
So,
By paying due attention to the sign of acceleration, this equation can also be applied to the problems of uniform retardation. In this case, a will be replaced by –a.
2.
This equation gives the displacement of the body in time t.
Consider a body moving with an initial velocity u having acquired a velocity v in time interval t, such that a is its uniform acceleration.
Let the displacement of the body in this time be S.
The displacement of the moving body in time t can be found out by considering its average velocity. Since the initial velocity of the body is u and its final velocity is v, the average velocity is given by:
Average velocity
Also, Displacement = Average velocity × Time
From the first equation of motion, we have, v = u + at.
Substituting this value of v in equation (1), we get
3.
This equation gives the velocity acquired by a body after it displaces through ‘s’.
Consider a body moving with an initial velocity u having acquired a velocity v after displacing through s. The uniform acceleration of the motion is a.
Let the displacement of the body in this time be S.
The displacement of the moving body in time t can be found out by considering its average velocity. Since the initial velocity of the body is u and its final velocity is v, the average velocity is given by:
Average velocity
Also, Displacement = Average velocity × Time
And from the first equation of motion, we have:
Substituting this value of t in equation (1), we get:
4.
This equation gives distance travelled by a body second.
Consider a body moving with uniformly accelerated motion having acceleration a. The distance of a particle in time t is given by ,
where u = initial velocity, at time t = 0
If are the distances of the particle in n and n – 1 seconds, then distance of the particle in second is,
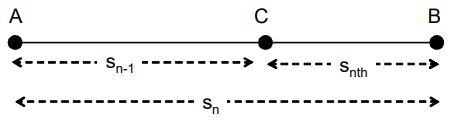
Now,
1.8 GRAPHICAL REPRESENTATION OF MOTION
When you see, you learn faster and understand better. The data from any measurement can be made more informative when presented in the form of a graph. In this section, we study the importance of graphs for describing the motion of a body.
What is a Graph?
A geometrical relationship between two quantities plotted on the x-axis and y-axis is called a graphical plot, or simply a graph.
One of the two quantities to be plotted can be changed independently, while the other depends on it. The quantity which can be changed independently is called the independent quantity, while the other which depends on it is called the dependent quantity. Generally, the independent quantity is plotted on the x-axis, and the dependent quantity on the y-axis. For example, if we want to draw a graph between the number of runs scored and the number of overs bowled in a cricket match, then the number of overs is the independent quantity, and the number of runs scored is the dependent quantity.
How a Graph is plotted
Graphs are plotted on specially designed graph papers. The whole sheet of the commonly used graph paper is divided into squares of 1 cm sides. Each side of such squares is further subdivided into millimetres. The lines showing millimetre markings are generally light incolour. To draw a graph, we generally proceed as follows.
i) Drawing the axes
If both the quantities to be plotted are positive, then draw two perpendicular lines intersecting each other at one point. This point of intersection is called the origin. The
horizontal axis is called the x-axis, while the vertical axis is called the y-axis. If one of the two or both the quantities are negative, then the axes are drawn so that the origin is in the middle of the paper.
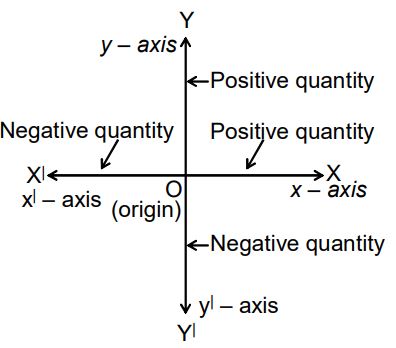
While plotting, it should be remembered that all positive quantities are plotted on the right and upwards of the origin. The negative quantities are plotted on the left and downwards of the origin.
The independent quantity is plotted on the horizontal (OX or OX’) axis, and the dependent quantity is plotted on the vertical (OY or OY’) axis.
ii) Choosing the Scale
The quantities to be plotted on the two axes are generally much bigger than the graph paper. So, for each axis, a convenient scale is chosen so that the whole range of the quantities can be plotted on a certain length of the axis. The choice of scale is made so that the plotted graph satisfies the following conditions
a) The curve or line of the graph should cover the major portion of the area enclosed by the two axes.
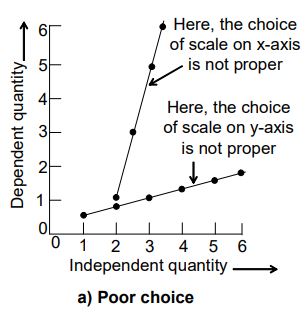
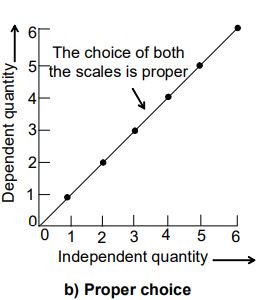
The choice of scales on the two axes:
i) a poor choice ii) a proper choice
b) If the plot is a straight line, it should have an inclination of about 45°, i.e., the graph should lie in the middle of the quadrant enclosed by the two axes of the scales. The effect of a good and a bad choice of the scales on the graph is shown in above figure.
iii) Plotting of the given Data
The given values of the two quantities are then plotted in the form of points on the graph paper. These points are then joined by a smooth line/curve to get the desired graph.
iv) Calculations from the Graph
The graphs can then be analysed to obtain certain parameters, such as, the slope and the intercept.
Usefulness of Graphs
Graphs are useful in the following ways:
i) A graphical plot can present a huge amount of data in a compact form.
ii) A graphical plot shows the geometric dependence of one quantity over the other. For example, a graph immediately tells us whether the dependent quantity (on the y-axis) is a linear or non-linear function of the independent quantity (on the x-axis).
iii) A graphical plot makes the comparison of different sets of data easier.
iv) A graph can be used to obtain the value of one quantity for a certain specified value of the other.
1.9 DISPLACEMENT – TIME GRAPHS
i) Displacement-time Graph of a body at Rest
The position of a body at rest remains unchanged with time. Let us consider a body at a distance d from a reference point in a particular direction. Then from the figure,
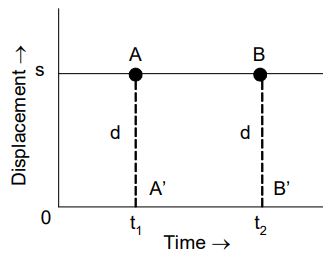
Displacement–time graph for a body at rest
At time t = 0 Displacement = d
At time t = Displacement = d
At time t = Displacement = d
Thus, there is no change in the displacement of the body with time.
For a body at rest, the displacement-time graph is a straight line parallel to the time-axis. From this graph, one can write
Velocity of the body at rest
Thus the velocity of a body at rest is zero
ii) Displacement-time Graph of a body moving with Uniform Velocity
The displacement-time graph of a body moving with uniform (constant) velocity is a straight line inclined to the time-axis at a certain angle.
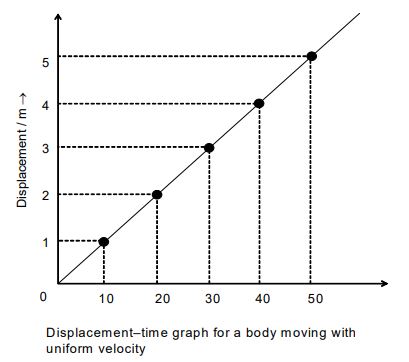
The slope of the displacement-time graph of a body moving at uniform velocity is equal to the velocity of the body.
Here, the slope of the straight line plot is positive.
Therefore the velocity of the body is positive.
iii) Displacement-time Graph of a body moving with an Increasing, Non-Uniform Velocity
The displacement-time graph of a body moving with non-uniform velocity curve.
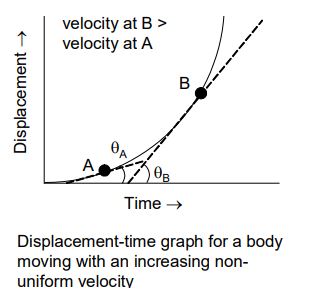
Here, the slope of the curve increases with time. So, the velocity of the body increases with time,
i.e., Velocity at B > Velocity at A
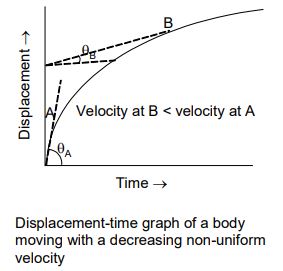
iv) Displacement-time Graph of a body moving with Decreasing, Non-Uniform Velocity
The displacement-time graph of a body moving with a decreasing non-uniform velocity is a curve. Here, the slope of the curve decreases with time. So, the velocity of the body decreases with time, i.e., Velocity at B < Velocity at A
v) Displacement-time Graph of a body moving with a Change of Direction
When a body moves with a change of direction, its displacement-time graph is not the same as its distance-time graph. This is illustrated by taking the following example.
A boy goes from his house to the post office with uniform speed. After mailing the letter, he comes back to his house with the same speed. To draw the distance-time and displacement-time graphs of the boy, let us proceed as follows:
Let the distance between the house and the post office be x and time taken to reach post office from his house be t.
Note: Remember the distance-time and displacement-time graphs of a moving body are similar only when the body moves along a straight line in its positive direction
without changing its direction.
a) The boy comes back to his house with the same speed. This means, he takes equal time for the return journey. Then, the distance-time graph for the total journey is shown in the figure.
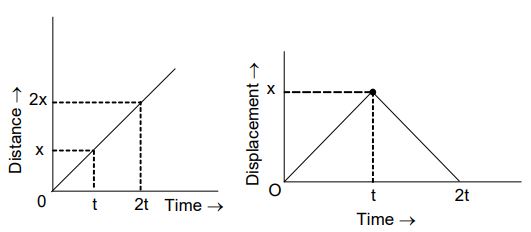
b) The body goes from his house to the post office and then back to his house at the same speed. So, the displacement of the boy at the end of the journey is zero. The displacement-time graph of the boy’s journey is shown in the figure.
Note that the boy is not moving in a straight line (there is a change of direction). So the displacement-time graph is different from the distance-time graph.
1.10 SPEED-TIME GRAPHS (OR VELOCITY- TIME) GRAPHS
The geometrical relationship between the velocity of a body and the time from the start is called a velocity-time graph.
The shape of the velocity-time graph of a body depends upon the nature of its motion. For a motion along a straight line in a particular direction the slope of a velocity-time graph is equal to the acceleration of the body.
Different types of velocity-time Graphs
For a straight line motion, there can be eight different types of speed-time (or velocity-time) graphs. These are described in the figure given in the next page:
Uses of speed-time or velocity -time graphs of a straight line motion
Speed-time or velocity-time graphs can be used for
i) determining the speed or velocity of the body at any particular point of time.
ii) determining the acceleration of the body. The slope of a speed-time (or velocity-time) graph equals the acceleration of the body.
iii) determining the total distance (or displacement) travelled by the body in a given time interval.
Calculation of distance travelled from speed-time graphs
How to calculate the distance travelled in a certain time interval from a speed-time graph
Speed-time graphs can be used for calculating the distance travelled by the moving body in a certain time. The methods of calculating distance from speed-time graphs in some typical cases are described below
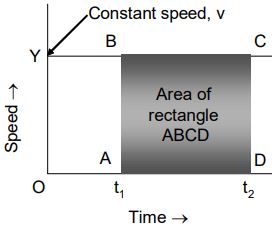
1. When a body moves with a constant speed in a straight line
The speed-time graph for a body moving with a constant speed is a straight line parallel to the time-axis
|
Conditions under which the body moves |
Description of the graph |
Speed –time graph, or Velocity-time graph |
|
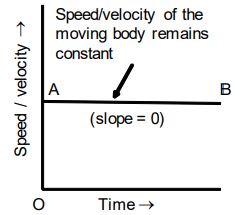
1. When the speed/velocity remains constant |
Straight line parallel to the time -axis (x-axis) Slope of the speed-time graph gives acceleration of the body. Therefore, the acceleration of a body moving with a constant speed (or velocity) is zero. |
|
|
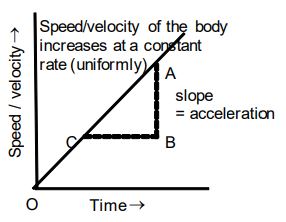
2. When the initial speed/velocity is zero, and the speed/velocity increases uniformly (at a constant rate) with time. |
Straight line sloping upwards and passing through the origin. Slope of the straight line is positive. Therefore, the body moving with a uniformly increasing speed/velocity has uniform acceleration. |
|
|
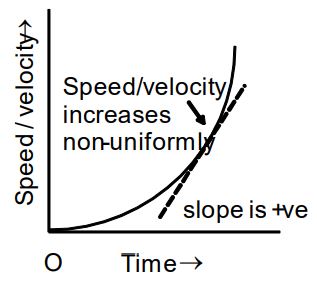
3. When the velocity/speed increases non-uniformly i.e.,, when the body is under non-uniform acceleration |
Speed–time or velocity -time graph in this case is a curve moving upwards. Slope of the curve is positive and time graph in this case is a curve moving upwards. Slope of the curve is positive and increases with time. Positive slope of the curve at any point is equal to the acceleration of the body. So, the acceleration of the body increases with time i.e., body is under non-uniform acceleration |
|
|
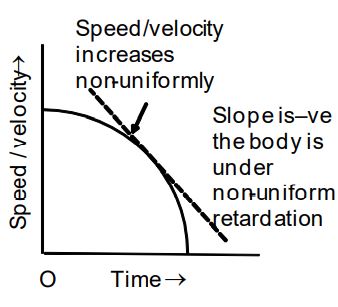
4. When the velocity/ speed increases non-uniformly i.e, when the body is under-uniform retardation |
Speed-time or velocity -time graph is a curve moving downwards. Slope of the curve is negative, and increases with time. Negative slope of a speed-time (or velocity-time) curve gives retardation (negative acceleration ) of the body. Here, the retardation increases with time, i.e., the body is under non-uniform retardation |
|
|
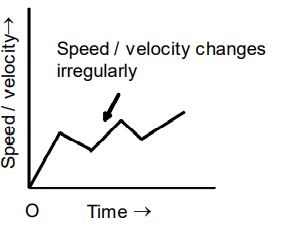
5. When the speed/velocity increases and decreases alternatively, i.e,, the speed/velocity changes alternatively. |
Speed-time or velocity–time graph in a zig-zag curve. The body is under uniform acceleration and retardation alternatively. |
|
|
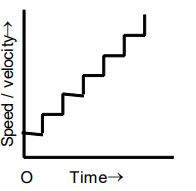
6. When the speed/velocity increases in a stepwise manner. |
The speed-time or velocity-time graph looks like a staircase. The body has alternatively infinitely large acceleration (vertical motion) and zero acceleration (horizontal motion). |
|
Conclusions :
i) If velocity–time graph is a straight line but moving away from velocity time axis, then:
a) Body is moving with variable velocity.
b) It has uniform acceleration, which can be found by the slope of graph.
c) Displacement can be found by finding area under the velocity-time graph.
d) If slope is positive, then the body has positive acceleration and vice–versa.
ii) If the velocity–time graph is a curve, then:
a) The body has variable velocity and variable acceleration.
b) Area under the curve represents displacement.
c) Acceleration at any instant can be found by finding slope at that point.
Calculation of the distance travelled by a body moving at constant speed in the time interval,
Speed of a body is given by,
or, Distance travelled = Speed × Time taken
Let us consider a body moving with a constant speed v.
If the body travels from time to time then
Time interval =
Therefore,
Distance travelled by the body in the time interval
To get the values of v, and from the speed-time graph proceed as follows.
Draw perpendiculars from the points A and D on the time-axis. Let these perpendicular intersect the straight-line graph at points B and C respectively. Then
Speed of the body = v = OY = AB = CD
Time, = OA
Time, = OD
Substituting the values of v and in the equation,
we get
Distance travelled in the time interval = AB × AD = Area of the rectangle ABCD
The area of rectangle ABCD is also called the area under the graph.
Thus, the distance travelled by a body in a certain time interval is equal to the area under the speed-time graph for the given time interval.
Note: The area of the rectangle under the graph in a speed-time graph is not area in the mathematical sense of the word. To understand this, let us recall that in geometry, the area of a rectangle is given by the product of length × breadth and both are measured in units ofdistance e.g., metre. So, the unit of area is e.g., square metre.
In speed-time graphs, the lengths on the two axes do not describe the ‘distance’. In the speed-time graphs, the length on the x-axis describes the time interval, and the length on the y-axis describes speed. The time interval is measured in units of time, generally second, and the speed in units of distance per unit time, generally metre per second. Therefore,
Area of the rectangle in a speed-time graph is given by
Area = Speed × Time
2. When a body moves with uniform acceleration
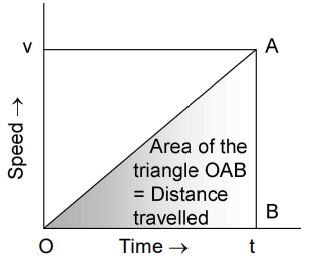
The above figure shows the speed-time graph of a body when its speed increases uniformly from zero to v in time t. Then, the average speed is given by.
The distance travelled by the body is then given by,
Distance moved by the body = Average speed × Time interval = .
From the speed-time graph, v = AB and t = OB
Then, Distance travelled in time
or, Distance travelled in time t = Area of the triangle OAB
When a body moves with uniform retardation
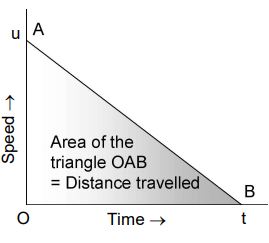
The above figure shows the speed-time graph of a body when its speed decreases uniformly to zero in time t.
Then, the average speed of the body is given by.
Then,
Distance travelled by the body in time t
From the speed–time graph, u = OA and t = OB
Substituting the values of v and t in above equation, we get
Distance travelled in time t from the start
Hence, Distance travelled in time t from the start = Area of the triangle OAB
Note: When the initial or the final speed of a body is zero, and the speed increases or decreases uniformly, then the area of the triangle formed by the speed-time graph and the time-axis is equal to the distance travelled by the moving body in time t.
4. When the initial speed is not zero and the speed increases uniformly
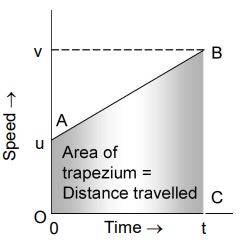
Let the initial speed of the body be u, and let it increase uniformly to v in time t.
Then,
Distance travelled by the body in t = Average speed × Time interval
But,
So, Distance travelled by the body in time
From the speed-time graph
u = OA v = BC and, t = OC
Substituting these values in above equation, we get
Distance travelled by the body in time
or, Distance travelled by the body in time t = Area of the trapezium OABC
5. When the speed decreases uniformly and the final speed is not zero
Let the initial speed of the body be u, and decrease uniformly to v in time t. Then,
Distance travelled by the body in time t = Average speed × Time interval
So,
Distance travelled by the body in time
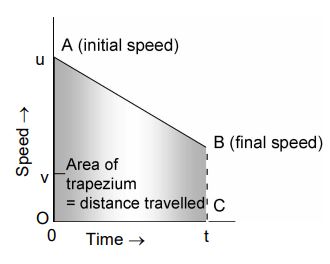
u = OA, v = BC, and t = OC
Substituting these quantities in the above equation, we get
Distance travelled by the body in time
or, Distance travelled by the body in time t = Area of the trapezium OABC.
Note: When the speed of a body increases or decreases uniformly and its initial or the final speed is not zero, then the area of the trapezium formed by the speed time graph for the given time interval is equal to the distance travelled by the body in that time interval.
Speed-time and velocity-time graphs of a body thrown vertically upward.
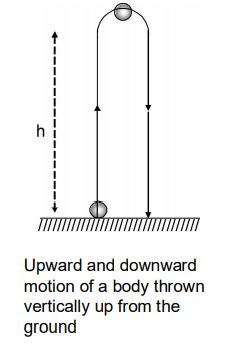
Consider a body thrown vertically upwards. As it goes up, its speed decreases, becomes zero at the highest point and then increases while coming down. The speed-time graph of such a body is shown in figure.
Taking upward direction as the positive direction, the velocity of the body in the upward direction is positive. As the body moves upwards, its velocity decreases, becomes zero at the highest point, and then becomes negative while coming down. The velocity-time graph of such a body is shown in figure.
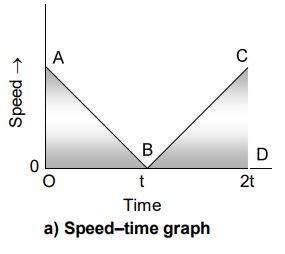
The shaded area gives the distance travelled by the body.
Distance travelled = Area OAB + Area BCD
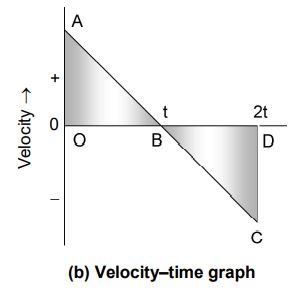
The shaded area in the graph gives the displacement.
Displacement = Area OAB + Area BCD = Area OAB – Area OAB = 0
Speed-time and velocity-time graphs of a body thrown upwards.
It should be noted that the distance travelled by the body is positive while the displacement is zero.
1.11 ACCELERATION – TIME GRAPHS
Figure (i) represents an acceleration–time graph, AB coinciding with time axis. From the figure it is clear that acceleration of the body is zero, and hence, it is moving with a uniform velocity.
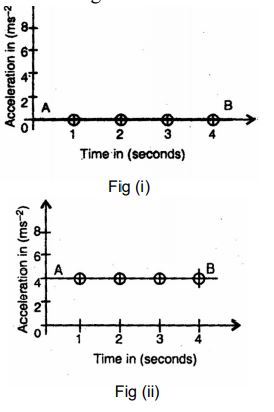
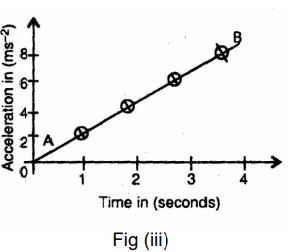
Figure (ii) represents an acceleration–time graph, parallel to time axis. From figure it is clear that as acceleration does not change, therefore body is moving with a uniform acceleration and variable velocity.
The area of graph, i.e., Acceleration × Time gives change in velocity.
Figure (iii) represents an acceleration–time graph moving away from time as well as acceleration axis. From the graph it is clear that the body is moving with variable velocity and variable acceleration. Area of the graph gives change in velocity.