Force and Laws of Motion

2.1 INTRODUCTION
The ice boats fly across the frozen lake at some 96 kmph. Pretty amazing! We could use kinematics to describe a boat’s motion with pictures, graphs, and equations. By defining position, velocity, and acceleration and dressing them in mathematical clothing, kinematics provides a language to describe how something moves. But kinematics would tell us nothing about why the boat accelerates briskly before reaching a top speed. For the more fundamental task of understanding the cause of motion, we turn our attention to dynamics. Dynamics joins with kinematics to form mechanics, the general science of motion.
The theory of mechanics originated in the mid – 1600s when Sir Isaac Newton formulated his laws of motion. These fundamental principles of mechanics explain how motion occurs as a consequence of forces. Newton’s laws are more than 300 years old, but they still form the basis for our contemporary understanding of motion.
2.2 FORCE
Consider a ball lying on the table. The ball remains at rest if nobody disturbs it. If your push the ball, it begins to move in a straight line with a certain speed. From this example, we find that the push acting on the ball has changed the speed of the ball from zero to a certain
value.

Consider a ball rolling over the surface of a floor with a certain speed. Now put your hand in the path of the rolling ball. The hand stops the ball. So, we find that the speed of the ball changes when we apply a push on it.

Place a bat at some angle in the path of an oncoming ball. We find that the direction of motion of the ball changes when it strikes the bat.

Consider a spring whose one end is fixed on a wall. Now pull the spring. The spring is stretched, i.e., the size of the spring changes, when pulled.
From these examples, we see that the push or pull acting on the body changes the speed of the body or direction of motion of the body or shape and size of the body. This pull or push acting on the body is known as force.3
A force is a pull or push acting on the body which changes or tends to change the speed of the body or direction of motion of the body, or the shape and size of the body.

Effects of force
i) Force can cause motion in a stationary object When a force is applied on a stationary object it can make it move. For example, if you push a book placed on a table, it starts moving. When you pull a cart, it starts moving.
However, it is not necessary that a force can always make a stationary body move. For example, if you try to push the wall of your classroom, it will not move. For that matter even if all the boys in your class push the wall, it will not move. The reason being, the force applied by all of you is not sufficient to move the wall. However, your action of push, i.e., the force has at least tried to move the wall. 

ii) Force can stop the moving objects or slow them down
Imagine your friend is riding a bicycle. If you pull his bicycle from behind, it slows down and may stop altogether. It means, if you apply force in the direction opposite to direction of moving body, the body slows down. Similarly, if we apply brakes to a moving bicycle, it first slows down and then stops. We ourselves have to apply force to stop our bodies while running. A cricket fielder stops a ball by applying force in the direction opposite to that of
the ball.
From above examples, it is clear that a force may stop a moving body or may reduce the speed of the moving body.
iii) Force can make a moving object move faster
Imagine a cart-puller pulling a cart up a sloping road slowly. If you push the cart from behind, then the cart will start moving fast. Similarly, when a moving vehicle is accelerated by pressing the accelerator, it starts moving faster. When a football player hits the moving football, the ball starts moving faster. When the horse pulling a tonga applies greater force, the tonga moves faster.
iv) Force can change direction of moving objects
When a cricket player hits the ball with his bat, his force changes the speed as well as the direction of the ball. Similarly, a football player changes the direction of the moving ball by angling his foot. You can change the direction of your moving bicycle by applying force on its handle on the right or left hand side.
v) Force can change the shape of objects
Imagine a spring fixed in a wall with a nail. When we pull the spring, it gets stretched and hence its shape changes. Similarly, when we crumple a piece of plain paper, its shape changes. By applying force, you can shape plasticine in to any form. From the above examples, we are in a position to define force.
Force is an external agent which changes or tends to change the state of rest or uniform motion of a body or changes its direction or shape.

2.3. NEWTON’S FIRST LAW OF MOTION
Let us suppose that a book is lying on a table. It is at rest.
Can the book change its position by itself?
Obviously, no.
The book will not move by itself, unless you push or pull or lift it. Thus, the position of the book can change its position, only when some force is applied.
A person riding a bicycle along a level road does not come to rest immediately after he stops pedalling, unless he applies the brakes. Here, on applying the brakes, the state of motion is changed to a state of rest.
These examples contribute to Newton’s First law of motion.
A body continues to be in the state of rest or of uniform motion along a straight line unless it is compelled by an external force to change its state.

“Objects keep on doing what they are doing, unless they are acted upon by an unbalanced force”.
The of Newton’s First law of motion introduces the concept of inertia and defines force.
Therefore the first law of motion is also known as the law of inertia.
2.4 INERTIA
From Newton’s first law of motion, it is clear that a body is unable to change its state of rest or motion by itself. This property of the body is known as inertia.

Inertia of a body may be defined as the tendency of a body to oppose any change in its state of rest or uniform motion.
For example, a book lying on a table will remain where it is placed unless it is displaced. Similarly, a ball rolling on a horizontal surface keeps on rolling unless the force of friction between the ball and the surface stops it.
Mass and inertia
Inertia is an inherent property of each body by virtue of which it has a tendency to resist the change in its state of rest or state of uniform motion. The property of inertia is due to the mass of a body. The greater the mass, the greater is the inertia of a body.
For example, if a body has a mass of 1kg and another body has a mass of 20 kg, then the body having 20 kg mass will have more inertia since its mass is more.

Types of inertia
Inertia can be divided into three types.
i) Inertia of rest
ii) Inertia of motion
iii) Inertia of direction
Inertia of rest
The tendency of a body by virtue of which it cannot change its state of rest by itself is called inertia of rest.
Examples:
i) A person in a car tends to fall backward when the car starts suddenly: When a person is sitting or standing in a stationary car, both the car and the person are at rest. When the car starts suddenly, the lower part of the person’s body starts moving forward with the car. But the upper part of the body tends to remain in the state of rest due to inertia of rest. As a result, he falls backward.
ii) On shaking or giving jerks to the branches of a tree, the fruits fall down: Initially both the tree and the fruits hanging to its branches are in a state of rest. When the branches of the tree are shaken, it is set into motion while the fruits remain in a state of rest due to the inertia of rest. Thus, the fruits get detached from the branches and fall down due to the pull of gravity.
iii) The carpet is beaten with a stick to remove the dust particles: When the carpet is beaten with a stick, the fibres of the carpet come in motion and hence move forward. On the other hand, the dust particles remain at rest due to inertia of rest. Therefore, they fall down.
Inertia of motion
The tendency of a body by virtue of which it cannot change its state of motion by itself is called inertia of motion.
Examples:
i) A person in a moving car tends to fall forward when the car stops suddenly: When a person is sitting or standing in a moving car, both the car and the person are in the state of uniform motion. When the car stops suddenly, the lower part of the person’s body comes to rest along with the car. The upper part of his body tends to remain in the state of motion due to its inertia of motion. As a result, the person leans forward.

ii) A girl jumping out of a speeding van may fall forward: This is because as the foot of the girl touches the ground, the lower part of her body comes to rest while the upper part of his body remains in motion due to inertia of motion.
iii) A cyclist does not come to rest immediately after she stops pedaling: A cyclist riding along a road does not come to rest immediately after she stops pedaling. The bicycle continues to move forward due to the inertia of motion.

iv) When a rotating fan is switched off it continues to rotate due to inertia of motion.
Inertia of direction
The tendency of a body to oppose any change in its direction of motion by itself is known as inertia of direction.
Examples:
i) When a fast-moving bus negotiates a curve on the road, passengers fall towards the centre of the curved road. This is due to the tendency of the passengers to continue to move in a straight line.
ii) A stone tied to a string and whirled along a circular path flies off tangentially due to inertia of direction, if the string breaks.

iii) While sharpening a knife, sparks fly off tangentially from the grinding stone, due to inertia of direction.
iv) Mud sticking to a cycle tyre flies off tangentially. That is why mud-guards are provided on the front and rear wheels of the cycle.

2.5 LINEAR MOMENTUM
Consider two balls A and B. Let ball A be heavier than ball B. i.e. mass ($m_1$) of ball A is greater than the mass ($m_2$ ) of the ball B. Suppose both balls are moving with
same velocity $\overrightarrow{v}$ .The force required to stop ball A is more than the force required to stop ball B. This shows that the heavier ball has more quantity of motion than the lighter ball. Thus, the quantity of motion of a body is directly proportional to the mass of the body.
Now consider two balls of same mass moving with different velocities. The force required to stop the fast-moving ball is more than the force required to stop the slow-moving ball. So the quantity of motion of the body is directly proportional to the velocity of the ball.
Conclusion: The quantity of motion of the moving body is proportional to
i) mass of the body        ii) velocity of the body.
This quantity of motion possessed by a moving body is known as momentum of the body (or) the total quantity of motion contained in a body is called momentum.
Mathematical expression: Momentum of a body is equal to the product of the mass (m) of the body and the $\text{ velocity }\left(\overrightarrow{\mathrm{v}}\right)\text{ of the body. It is denoted by }\overrightarrow{\mathrm{P}}\text{ . }$

$\boxed{\begin{array}{c}\text{ Thus, momentum }=\text{ mass }\times \text{ velocity }\\ \overrightarrow{\mathrm{P}}=\mathrm{m}\overrightarrow{\mathrm{V}}\\ \mathrm{Momentum} \mathrm{is} \mathrm{a} \mathrm{vector} \mathrm{quantity}\end{array}}$

Note:
i) Momentum is a vector quantity.
ii) The direction of momentum of a body is same as that of the direction of the velocity of the body.
iii)The SI and CGS units of momentum are kg-m/ s and gm-cm/s respectively.
2.6 NEWTON’S SECOND LAW OF MOTION
Newton’s second law gives the quantitative definition of force. In other words, it measures force.
According to Newton, when force is applied upon a body, then acceleration is produced.

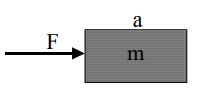
The acceleration produced in a body is
a) directly proportional to the force acting on it $\text{ i.e }\mathrm{a}\propto \mathrm{f} ––––\left(\mathrm{i}\right)$

b) inversely proportional to the mass of the body $\text{ i.e. }\mathrm{a}\propto \frac{1}{\mathrm{m}} –––––\left(ii\right)$

from (i) and (ii) we have $\propto \frac{\mathrm{F}}{\mathrm{m}}\Rightarrow \mathrm{F}\propto \mathrm{ma}\Rightarrow \mathrm{F}=\mathrm{k} \mathrm{m} \mathrm{a} ––––––\left(\mathrm{iii}\right)$

Where k is constant.
Now if F = 1 unit of force
m = 1 unit of mass and
a = 1 unit of acceleration then k = 1 and hence F = ma ________ (iv)
So, Force acting on the body = mass of the body × acceleration produced in the body
Newton’s second law states that: “The magnitude of the resultant force acting on a body is proportional to the product of the mass of the body and its acceleration. The direction of the force is the same as that of the acceleration”.

Newton’s second Law in terms of momentum
The rate of change of momentum of an object is proportional to the net force applied on the object. The direction of the change of momentum is the same as the direction of the net force.
Derivation F = ma
Consider a body of mass m moving with initial velocity u. Let a force F act on the body for time t so that the velocity of the body after time t is v.

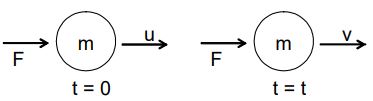
Initial momentum of the body ($P_i$)= m u
Final momentum of the body (${\mathrm{P}}_{\mathrm{f}}$) = m v
Now, change in momentum of the body $={\mathrm{P}}_{\mathrm{f}}-{\mathrm{P}}_{\mathrm{i}}=\mathrm{mv}-\mathrm{mu}=\mathrm{m}(\mathrm{v}-\mathrm{u})$
Time taken for this change in momentum = (t – 0) = t
$\therefore$ Rate of change of momentum $=\frac{\text{ change of momentum }}{\text{ time taken }}$

$=\frac{\mathrm{m}(\mathrm{v}-\mathrm{u})}{\mathrm{t}}=\mathrm{ma}=\mathrm{F}\left(\because \mathrm{a}=\frac{(\mathrm{v}-\mathrm{u})}{\mathrm{t}}\right)$

Note: Newton’s first law of motion is a special case of
Newton’s second law of motion
We know that $\mathrm{F}=\mathrm{ma}=\mathrm{m}\left(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}\right)$

If velocity of the body is constant i.e. u = v, then $F=m\left(\frac{v-v}{t}\right)=0$

Thus, no force is required to move a body with constant velocity or uniform velocity. If u = 0, then v is also zero; it means the body will remain at rest if no external force is applied on the body. This is the first law of motion.
Units of Force

$\begin{array}{l}\text{ S.I unit of force }=\mathrm{kgm}/{\mathrm{s}}^2=\text{ newton }\\ \text{ C. G.S unit of force }=\mathrm{gcm}/{\mathrm{s}}^2=\text{ dyne. }\end{array}$

$\boxed{\begin{array}{r}\therefore 1\text{ newton }\left(\mathrm{N}\right)=1\mathrm{kgm}/{\mathrm{s}}^2\\ 1\text{ dyne }=1\mathrm{gcm}/{\mathrm{s}}^2\end{array}}$

Note:
i) 1 newton is that much force which produces an acceleration of 1 $m/s^2$ in a body of mass 1 kg.
ii) The force is said to be 1 dyne if it produces 1 $cm/s^2$ acceleration in a body of 1g mass.
Relation between newton and dyne

$1\text{ newton }\left(\mathrm{N}\right)=1\mathrm{kgm}/{\mathrm{s}}^2=1000\mathrm{g}\times 100\mathrm{cm}/{\mathrm{s}}^2=100000\mathrm{gcm}/{\mathrm{s}}^2={10}^5\mathrm{gcm}/{\mathrm{s}}^2={10}^5\text{ dyne }$

Gravitational Units of force
Gravitational units of force is the force which produce an acceleration equal to the acceleration due to gravity in a unit mass.
a) Gravitational unit of force in S.I. system is kilogram weight or kilogram force.

$$\begin{gathered} 1\mathrm{kgwt}=1\mathrm{kg}\times 9.8\mathrm{m}/{\mathrm{s}}^2\text{ (on earth) } \\ 1\mathrm{kg}\text{ wt }\left(\mathrm{kgf}\right)=9.8\mathrm{kgm}/{\mathrm{s}}^2=9.8\mathrm{N} (\mathrm{on}earth) \end{gathered}$$

b) Gravitational unit of force in C.G.S. system is 1 gram weight or gram force.

$\begin{array}{l}1\mathrm{gwt}=1\mathrm{g}\times 980\mathrm{cm}/{\mathrm{s}}^2\text{ (on earth) }\\ 1\mathrm{gwt}=980\mathrm{gcm}/{\mathrm{s}}^2=980\text{ dyne (on earth) }\end{array}$

Some applications of Newton’s second law of motion
i) Lowering of hands while catching a ball
We know that force = rate of change of momentum

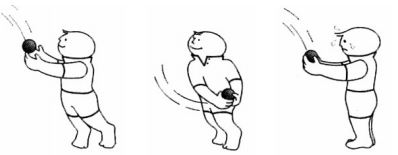
If a player does not lower his hands while catching the ball, the time to stop the ball is very little. So a powerful force has to be applied to change the momentum of the ball. When a player lowers his hands, the time to stop the ball is increased and hence less force has to be applied to cause the same change in the momentum of the ball. Therefore, the hands of the player are not injured.

ii) Cement floor cause more injury than heap of sand:

When a person falls on a cemented floor, the rate of change of momentum is very high
because the person is abruptly stopped i.e. stopped in a very short interval of time. Hence the person gets injured due to the application of a large force on his body due to the floor. On the other hand, when a person falls on a heap of sand, the sand yields under the weight of the person. As a result of this, the person comes to rest in a longer period of time. So the change in momentum takes place in longer interval of time. Hence a small force is exerted on the body of the person when he falls on a heap of sand. Therefore, he does not get injured.
iii) The use of seat belts in cars: These days all the cars are provided with seat belts for passengers to prevent injuries in case of an accident. In a car accident, a fast running car stops suddenly. Due to this the car’s large momentum is reduced to zero in a very short time. The stretchable seat belts worn by the passengers of the car increase the time taken by the passengers to fall forward. Due to longer time, the rate of change of momentum of passengers is reduced and hence less stopping force acts on them. So, the passengers may either not get injured at all or may get less injuries. It is obvious that seat belts reduce the passengers’ momentum more gently and hence prevent injuries.

2.7 IMPULSE
A large force which acts during a small interval of time is called impulsive force.
Impulse of a force is defined as the change in momentum produced by the given force and it is equal to the product of force and the time for which it acts.
According to Newton’s $2^{nd}$ law of motion

$\begin{array}{l}\overrightarrow{\mathrm{F}}=\mathrm{ma}=\mathrm{m}\left(\frac{\overrightarrow{\mathrm{v}}-\overrightarrow{\mathrm{u}}}{\mathrm{t}}\right)=\frac{\mathrm{m}\overrightarrow{\mathrm{v}}-\mathrm{m}\overrightarrow{\mathrm{u}}}{\mathrm{t}}\\ \Rightarrow \overrightarrow{\mathrm{F}}\mathrm{t}=\mathrm{m}\overrightarrow{\mathrm{v}}-\mathrm{m}\overrightarrow{\mathrm{u}}\end{array}$

Impulsive force = change in momentum.
Note: Impulse is a vector quantity, whose direction is same as that of force.
Unit: S. I. unit of impulse = N s or kg m/s
            C.G.S unit of impulse = dyne second or g cm/s
Example:
1) The force with which a hammer strikes a nail.
2) The force with which a bat hits a cricket ball.

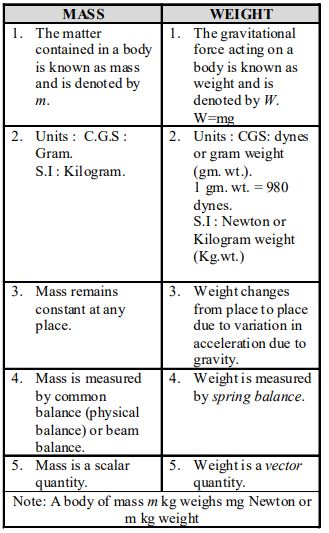
2.8 MASS AND WEIGHT
Mass: The mass of a body is the quantity of matter contained in it.
Weight: Any object dropped from some height always falls towards the Earth because of the gravitational force of the Earth. The force with which the Earth attracts an object towards its centre is known as force of gravitation of the Earth or gravity.
The force due to gravity on a body is known as its weight. Gravity of the Earth depends upon the mass of the Earth and its radius. Since the masses and radii of different planets are different, the gravity of different planets is different. Therefore, the weight of the body changes from one planet to another.
Weight is the force with which the Earth attracts a body. When the Earth attracts a body towards its centre with a force, the body accelerates towards the Earth with acceleration due to gravity.
Thus, the force with which body of mass ‘m’ is attracted by the Earth is given as
F = m × a, W = m × g = mg.
Where, ‘m’ is mass of the body and ‘g’ the acceleration due to gravity. This force is known as weight of the body.
Nature: Weight is a Vector quantity
Units: CGS system: dyne SI system: Newton

Note: Weight on moon $=\frac{1}{6}th$weight on earth.
Weightlessness
An object is said to be weightless when it falls freely under the action of gravity.
Note: A man falling freely under the action of gravity becomes weightless.
$(Asg=0\Rightarrow w=mg=0)$
Example: Let a stone piece be suspended from a spring balance suspended by a finger. The balance shows the actual weight of the stone.
When the balance is released from the fingers, the balance falls freely with the hanging stone piece. The balance shows a zero reading. This proves that the freely falling stone has become weightless.

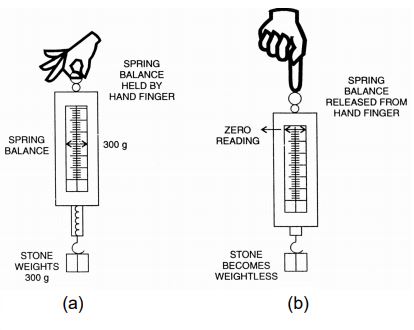
(a) The spring balance shows the weight of stone
(b) Freely falling spring balance with stone shows zero reading

Note:
i) During the state of weightlessness, the force of attraction due to gravity does not become zero. It is the apparent weight of the body which becomes zero during weightlessness.
ii) All freely falling bodies are in a state of weightlessness
Weightlessness in Space
When the astronaut in the spaceship is orbiting the earth, then both the astronaut and the spaceship, are in a continuing state of free fall towards the earth with the same acceleration due to gravity. Since the downward acceleration of the astronaut is the same as that of the
spaceship, he does not exert any force on the sides of the spaceship and appears to be floating “weightlessly”.
Thus, the astronaut is weightless with respect to the spaceship and a weighing machine kept in the space vehicle will show his weight to be zero.

2.9 NEWTON’S THIRD LAW OF MOTION
i) When a player kicks a football, the football moves forward and the foot of the player moves backward.
The force with which the football is kicked by the foot of the player, is known as action. Due to this action force, the football moves forward. On the other hand, the force exerted by the football on the football on the foot of the player, is known as reaction. Due to this reaction force, the foot of the player moves backward.
ii) When a ball falls towards the earth, the earth exerts a force ($F_1$) on the ball, to attract the ball towards its centre. On the hand, the ball exerts a force ($F_2$) onthe earth to move upward.

From these examples, we can conclude that, whenever two bodies collide with each other, they exert equal and opposite forces on each other. Out of these forces, one is known as action force and the other is known as reaction force.
The essence of this observation is tit for tat, also summarized as Newton’s $3^{rd}$ law of motion.
From above examples, we can conclude that “whenever two bodies have influence on each other they exert equal and opposite forces on each other, out of these forces.
One is known as action and other is known as reaction.
Newton’s Third law of motion – Statement
For every action, there is an equal and opposite reaction.
That is, Action = – Reaction
Note: Action and reaction force are equal in magnitude but opposite in direction.
i.e. Action = – Reaction
In other words, whenever two bodies interact with each other, the force exerted by the first body on the second body (called action) is equal and opposite to that exerted by the second body on the first body (called reaction).

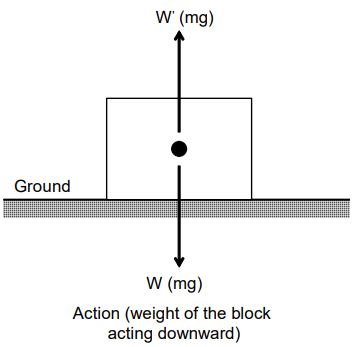
For example, a block when placed on the ground exerts a force acting downwards equal to its weight W (mg) on the ground (due to the attraction by the earth). This is called action. The ground exerts an equal and opposite force W (mg) on the block in the upward direction. This
is called reaction. From the above examples it is clear that,
Note:
i) Both action and reaction are forces [In this case, F = mg]
ii) Action and reaction act simultaneously, but act on different bodies. (In this case the block and the ground are two different bodies on which action and reaction act simultaneously)

iii) Action and reaction act on different bodies. For this reason, they cannot cancel each other.
iv)Action and reaction forces occur in pairs only. (In this case if the block was not placed on the ground, there would be no reaction.)
Action and reaction are always equal and opposite
To show that action and reaction are equal and opposite, set up two similar spring balances as shown in the figure.

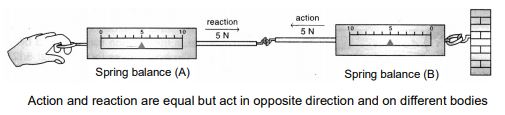
When spring balance A is pulled towards left, it exerts a force (say 5N) on the balance B. As a result, the spring balance B reads 5 N (action). The balance A also reads 5 N. This means the balance B also exerts a force of 5 N on the balance A (reaction). Therefore, we see that action
and reaction are equal but act in the opposite directions.
Examples of Newton’s third law of motion
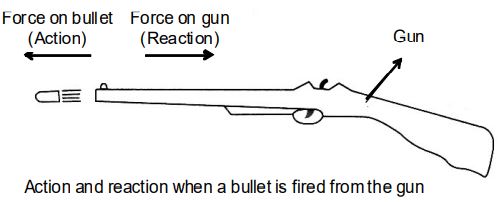
i) Recoiling of a gun: When a gun is fired, the bullet goes out due to the force applied on it through the trigger (this is action). According to Newton’s third law of motion, the gun recoils backwards due to the reaction acting on it in the opposite direction. This gives a backward jerk to the shoulder of the gunman

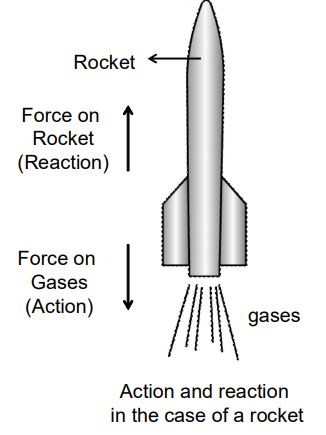
ii) Flying of Jet plane and rocket: In jet engines and rockets, the fuel is burnt to produce a large quantity of hot gases. These hot gases come out of a nozzle (a fine opening) with a great force (this is action). According to Newton’s third law of motion, the equal and opposite reaction pushes the jet aeroplane and rockets forward with a great speed (this is reaction)

iii) Swimming: When a person swims, he pushes the water in the backward direction with his hands (this is action). As the reaction, the water pushes the person in the forward direction with an equal force.

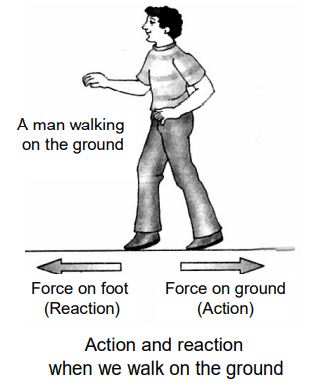
iv) Walking: When we walk on the ground, our foot pushes the ground backwards (this is action). In return, the ground pushes our foot forward with an equal and opposite force, (this is reaction). The forward reaction exerted by the ground on our foot makes us walk forward

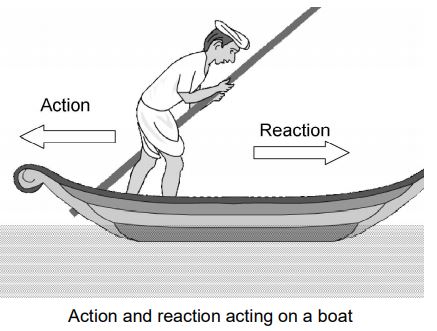
v) Rowing of a boat: When rowing a boat, the boatman pushes the water backwards with the oars (this is action). According to Newton’s third law of motion, the water exerts an equal and opposite push on the boat, which moves forward. (this is reaction). In fact, the harder the boatman pushes back the water with oars (i.e. the greater the action) the greater the reaction (force) exerted by the water and faster the boat moves forward.

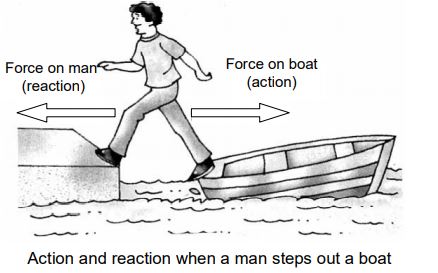
 vi) Tying of a boat: The boatman ties his boat before allowing passengers to disembark, This is due to the fact that when the passengers start disembarking (getting out of the boat), they push the boat backwards with their feet (this is action). The boat exerts an equal and opposite force on the passengers in the forward direction which enables them to move forward (this is reaction). Since the boat is in the water, it moves backward due to the action
(force) exerted by the passengers. So the boatman ties his boat to prevent the boat from sliding back in to the water.

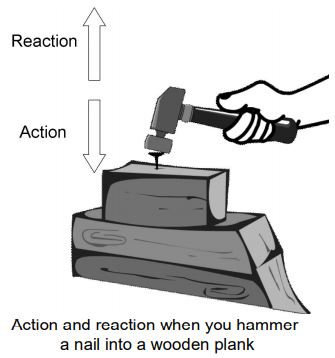
vii) Pain caused during hammering: We feel pain in our hand when we hammer a nail into a wooden plank. While hammering a nail, the force of the hammer on the nail is the action. According to Newton’s third law of motion the nail exerts an equal and opposite force on the hammer (the reaction). Since the hammer is held in our hand firmly, our hand experiences the force due to the reaction, and feels hurt.

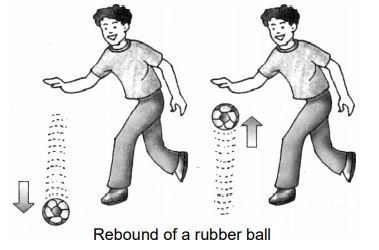
viii) Rebounding of a ball: When we strike a rubber ball against a hard floor, the ball exerts a force (called action) on the floor. According to Newton’s third law of motion, the floor exerts an equal and opposite force (called reaction) on the ball. The rubber ball, being light, rebounds.

ix) Pushing a wall: When we exert a force on a wall by pushing the palm of our hand against it (this is action); then, according to Newton’s third law of motion, the wall exerts an equal and opposite force (called reaction) on our palm, and therefore we feel pain in our hand.

2.10 LAW OF CONSERVATION OF MOME NTUM
According to this law, the total momentum of a system remains constant if no net external force acts on the system.
That is, momentum of a system. $\stackrel{r}{P}$ = constant, if net external force acting on it is zero

$\text{ (i.e. }\left.{\overrightarrow{\mathrm{F}}}_{\text{external }}=0\right)$

Conservation of momentum from third law of motion
If a number of bodies collide with one another, the total momentum of the bodies just before collision is equal to the total momentum just after collision.

Example: Let a moving ball collide with another stationary ball lying on the ground. Observe what happens after collision. The moving ball will slow down
i.e., its velocity decreases after colliding with the stationary ball. On the other hand, the stationary ball begins to move i.e. its velocity increases after collision.
We know, momentum of a body = mass of the body × velocity of the body $\left(i.e \stackrel{r}{P}=m\stackrel{r}{V}\right)$Therefore, the momentum of a moving ball decreases after collision and the momentum of the stationary ball increases after collision. Thus, we find that when two balls collide with
each other, then the moving ball loses momentum and the stationary ball gains momentum. The loss of momentum of one ball is equal to the gain of momentum of the other ball. However, the total momentum of these colliding balls, before and after the collision, remains the same. This is the law of conservation of momentum.
Derivation: Let us consider two marbles A and B having masses $m_1$ and $m_2$ moving with initial velocities, $u_1 and u_{2 }\left(u_1>u_2\right)$

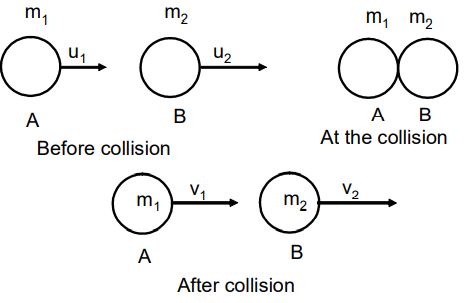
After collision, the two bodies move with velocities $v_1 and v_2$in the same direction, as shown in figure.
Momentum of body A before collision $={\mathrm{m}}_1{\mathrm{u}}_1$

Momentum of body B before collision $={\mathrm{m}}_2{\mathrm{u}}_2$

$\therefore$Total momentum of body A and B before collision$= {\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2$

Similarly:
momentum of body A after collision $={\mathrm{m}}_1{\mathrm{v}}_1$

momentum of body B after collision $=m_2{v}_2$

$\therefore$Total momentum of body A and body B after collision $=m_1{v}_1+m_2{v}_2$

Suppose the two marbles collide with each other for ‘t’ seconds.
The momentum of marble A before and after collision is ${\mathrm{m}}_1{\mathrm{u}}_1\text{ and }{\mathrm{m}}_1{\mathrm{v}}_1$ respectively.

$\Rightarrow$Change of momentum of body A during the collision $=m_1{v}_1-m_1{u}_1$

$\therefore$The rate of change of momentum during the collision of body A will be $=\frac{\text{ change of momentum }}{\text{ Time taken }}$$=\frac{m_1{v}_1-m_1{u}_1}{t}=\frac{m_1\left(v_1-u_1\right)}{t}$

Similarly, the rate of change of momentum of marble B will be $\frac{{\mathrm{m}}_2{\mathrm{v}}_2-{\mathrm{m}}_2{\mathrm{u}}_2}{\mathrm{t}}=\frac{{\mathrm{m}}_2\left({\mathrm{v}}_2-{\mathrm{u}}_2\right)}{\mathrm{t}}$

If the force exerted by marble A on B is $F_1$ and that by B on A is $F_2$ , then according to Newton’s $2^{nd}$ law of motion,

$\begin{array}{r}{\mathrm{F}}_1=\frac{{\mathrm{m}}_1\left({\mathrm{v}}_1-{\mathrm{u}}_1\right)}{\mathrm{t}}–––––\left(1\right)\\ {\mathrm{F}}_2=\frac{{\mathrm{m}}_2\left({\mathrm{v}}_2-{\mathrm{u}}_2\right)}{\mathrm{t}}–––––\left(2\right)\end{array}$

According to Newton’s $3^{rd}$ law of motion, the force exerted by marble A on marble B and marble B on marble A are equal and opposite to each other.

$\therefore F_1=-F_2$

$\begin{array}{l}\Rightarrow \frac{{\mathrm{m}}_1\left({\mathrm{v}}_1-{\mathrm{u}}_1\right)}{\mathrm{t}}=-\frac{{\mathrm{m}}_2\left({\mathrm{v}}_2-{\mathrm{u}}_2\right)}{\mathrm{t}}\\ \Rightarrow {\mathrm{m}}_1{\mathrm{v}}_1-{\mathrm{m}}_1{\mathrm{u}}_1=-{\mathrm{m}}_2{\mathrm{v}}_2+{\mathrm{m}}_2{\mathrm{u}}_2\\ \Rightarrow {\mathrm{m}}_1{\mathrm{v}}_1+{\mathrm{m}}_2{\mathrm{v}}_2={\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2\\ \text{ or, }{\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2={\mathrm{m}}_1{\mathrm{v}}_1+{\mathrm{m}}_2{\mathrm{v}}_2\end{array}$

i,e. total momentum before collision = total momentum after collision.

Note:
If the two bodies stick together after collision, then they move with common velocity v (say), then ${\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2={\mathrm{m}}_1{\mathrm{v}}_{+}{\mathrm{m}}_2\mathrm{v}$

$\Rightarrow v=\frac{m_1{u}_1+m_2{u}_2}{m_1+m_2}$

Examples to illustrate the law of conservation of momentum
i) Recoil of a gun
We have already explained the recoil of a gun, with the help of Newton’s third law of motion. However, the recoil of a gun can also be explained with the help of the law of conservation of momentum.
The bullet inside the gun and the gun itself forms a system. Thus, the system is (gun + bullet). Before firing, the gun and the bullet are at rest; therefore, momentum of the system before firing is zero.
When the bullet is fired, it leaves the gun in the forward direction with certain momentum. Since no external force acts on the system, the momentum of the system (gun + bullet) must be zero after firing. This is possible only if the gun moves backward with a momentum equal to the momentum of the bullet. That is why the gun recoils or moves backward.

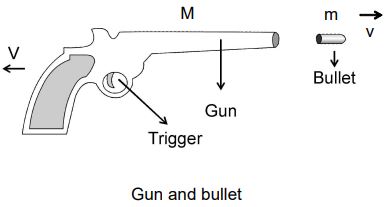
Recoil Velocity: The velocity with which the gun moves backward after firing a bullet is known as recoil velocity.
Calculation of Recoil Velocity of a gun:
Let mass of the bullet = m
velocity of the bullet after firing = $\overrightarrow{V}$

mass of the gun = M
Recoil velocity of the gun after firing = $\overrightarrow{V}$

Since the system is at rest before firing, the momentum of the system (gun + bullet) before
firing = 0
Total momentum of the system (gun + bullet) after firing

= momentum of gun + momentum of bullet 

$=\mathrm{M}\overrightarrow{\mathrm{V}}+\mathrm{m}\overrightarrow{\mathrm{v}}$

According to the law of conservation of momentum,

$\mathrm{M}\overrightarrow{\mathrm{V}}+\mathrm{m}\overrightarrow{\mathrm{v}}=0\Rightarrow \mathrm{M}\overrightarrow{\mathrm{V}}=-\mathrm{m}\overrightarrow{\mathrm{v}}\text{ or }\overrightarrow{\mathrm{V}}=-\left(\frac{\mathrm{m}}{\mathrm{M}}\right)\overrightarrow{\mathrm{v}}$

Negative sign shows that the direction of the velocity of the gun, after firing, is opposite to the direction of the velocity of the bullet.

ii) Movement of a rocket
The movement of a rocket in the upward direction can also be explained with the help of the law of conservation of momentum.

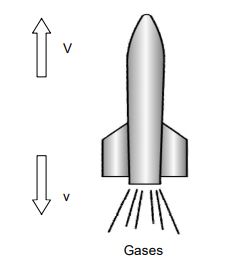
The momentum of a rocket before it is fired is zero. When the rocket is fired, gases are produced in the combustion chamber of the rocket due to the burning of fuel. These gases come out of the rocket with high speed. The direction of the momentum of the gases coming out of the rocket is in the downward direction. To conserve the momentum of the system (rocket + gases), the rocket moves upward with a momentum equal to the momentum
of the gases. The rocket continues to move upward as long as the gases are ejected out of the rocket.

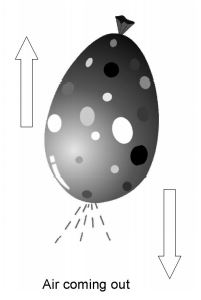
iii) Balloon moves forward when pricked with a pin
The momentum of the inflated balloon before it is pierced with a pin is zero. When it is pierced with a pin, air in it comes out with a speed in the backward direction. To conserve the momentum, the balloon moves in the forward direction.

iv) Man and boat
A man in a boat near a river bank is at rest

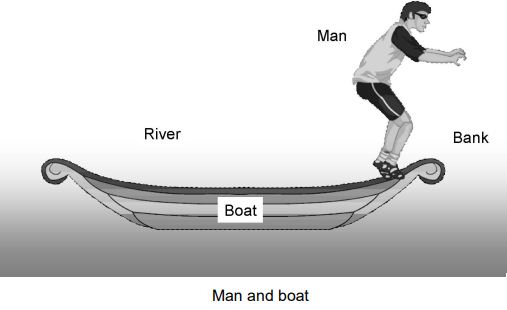
As the man jumps from the boat to the river bank, the boat is pushed behind.
In general, all cases involving action and reaction are an example of law of conservation of
momentum.
Action and reaction, being equal and opposite and acting simultaneously for same duration, have equal and opposite impulses. They produce equal and opposite changes of momentum in the pair of bodies involved. It keeps the total momentum of the two body system constant (conserved)
1. Momentum before collision = momentum after collision i.e ${\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2={\mathrm{m}}_1{\mathrm{v}}_1+{\mathrm{m}}_2{\mathrm{v}}_2$

2. After collision, if the two bodies stick together and move with common velocity v, then $\mathrm{v}=\frac{{\mathrm{m}}_1{\mathrm{u}}_1+{\mathrm{m}}_2{\mathrm{u}}_2}{{\mathrm{m}}_1+{\mathrm{m}}_2}$

3 . If the two bodies approach each other before collision, common velocity after collision is $v=\frac{m_1{u}_1-m_2{u}_2}{m_1+m_2}$

4. In the gun and the bullet system, momentum of bullet = momentum of gun.
Recoil Velocity of a gun can be written as $\mathrm{V}=-\left(\frac{\mathrm{m}}{\mathrm{M}}\right)\mathrm{v}$

where m = mass of the bullet
v = velocity of the bullet after firing
M = mass of the gun

2.11 TYPES OF FORCES
We classify force’s into two basic classes depending on whether the agent touches the object (or) not.
i) Long range force
Forces that act on an object without physical contact. This force is also called Action at a
distance force (or) Non – contact forces.
Example: A magnet attracts iron pins without touching them (Due to magnetic force)
Sun and earth attracts each other from a distance (Due to gravitational force)

Magnetic force and gravitational force are the examples of action-at-a-distance force (or) Non-contact forces.
There are many forces we will deal in further chapters in this section will introduce you to some of them. Many of these forces have specific symbols.

Weight $\left(\overrightarrow{W}\right)$ : The gravitational pull of the earth on an object on (or) near the surface of the earth is called weight.
The agent for weight force is the entire earth pulling on an object.
An objects weight vector always points vertically downwards, no matter how the object is moving.

weight $\overrightarrow{\mathrm{W}}=\mathrm{mg}$, m is mass, g is acceleration due to gravity
Note: weight is not the same thing as mass.
ii) Contact forces
These are the forces that act on an object by touching it at a point of contact.
Example: the bat must touch the ball to hit it.
A string must be tied to an object to pull it. Force exerted by a surface against an object that is pressing against the surface. Here surface is the agent.
Contact forces between two objects is made up of two forces.

a) Normal reaction $\left(\overrightarrow{N}\right)$ :

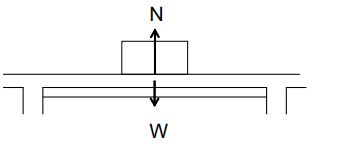
Two bodies in contact exert equal and opposite forces on each other.
The contact force is perpendicular to common surface and known as Normal reaction.
Example: Suppose you place your hand on a wall and lean against it. Does the wall exert a force on your hand? The Answer is yes the wall does exert force on you. It is not hard to see this if you examine your hand as you lean; your hand is slightly deformed and it will be more deformed so the harder you lean. This deformation is the direct evidence of force that the wall exerts on your hand.
Note: We are not using the word normal to imply that the force is “ordinary” force (or) to distinguish it from “abnormal force”. A surface exerts force perpendicular or normal to itself.

b) Force of friction $\left(\overrightarrow{f}\right)$ :

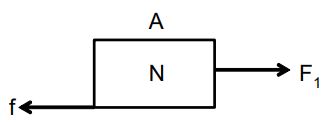
$F_1$ is the applied force, and f is the frictional force Friction, like the normal force, is exerted by a surface unlike the Normal force however, the frictional force is always Parallel to the surface, not perpendicular to it.
Friction is a force that always “opposes the motion” (or) it can be a force that keep an object “stuck” on a surface and prevents its motion.
Example: A rolling (or) sliding object, if not pushed slows down and eventually stop’s, this sort of behaviour is due to friction.
(Note: Details of friction will be dealt in coming chapters)

c) Spring force $\left({\overrightarrow{F}}_{sp}\right)$ :Springs exert one of the most basic contact forces.
A spring can either push (when it is compressed) or pull (when it is stretched).

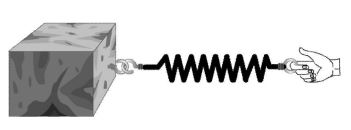
Spring force F = kx where k is spring constant and x is displacement.

d) Tension force $\left(\overrightarrow{T}\right):$ When a string (or) a rope (or) wire pulls an object, it exerts a contact force called Tension force the direction of the tension force is always in the direction of the string (or) rope.
Note: Tension force can only pull in the direction of the string if you try to push with a string, it will go slack and be unable to exert a force.

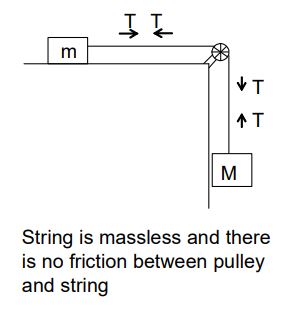
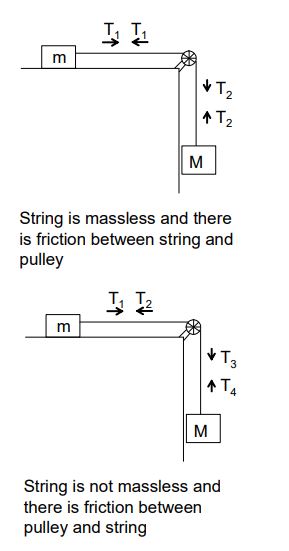
Case 1: If a string is inextensible the magnitude of acceleration of any number of masses connected through string is always same.
Case 2: If string is massless, the tension in it is same everywhere. However, if a string has a mass, tension at different points will be different.
Case 3: If there is friction between string and pulley, tension is different on two sides of the
pulley, but if there is no friction between pulley and string tension will be same on both sides of the pulley. Last two points can be understood in diagrams as follows.

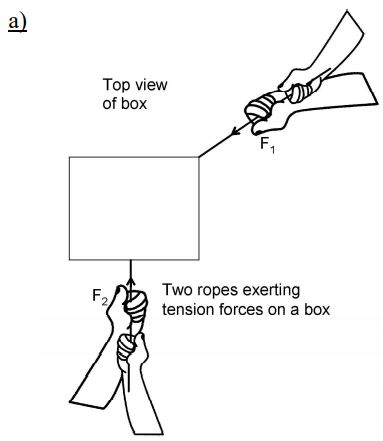
iii) Combining Forces
Figure shows a top view of a box being pulled by two ropes, each exerting a force on the box. How will the box respond? Experimentally, we find that when several forces ${\overrightarrow{F}}_1,{\overrightarrow{F}}_2,{\overrightarrow{F}}_3 .....$are exerted on an object, they combine to form a net force that is the vector sum of all the forces. 

${\overrightarrow{F}}_{\mathrm{net}}={\overrightarrow{F}}_1+{\overrightarrow{F}}_2-{\overrightarrow{F}}_3$

Mathematically, this summation is called a superposition of forces. The net force is sometimes called the resultant force. Figure shows the net force on the box.

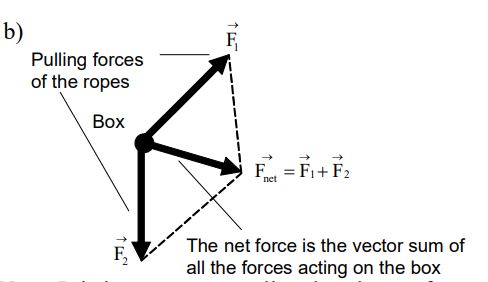
Note: It is important to realize that the net force ${\overrightarrow{F}}_{\mathrm{net}}$ is not a new force acting in addition to the original forces ${\overrightarrow{F}}_1,{\overrightarrow{F}}_2,{\overrightarrow{F}}_3 .....$ Instead, we should think of the original forces being replaced by ${\overrightarrow{F}}_{\text{net }}$.

2.12 IDENTIFYING FORCES
Force and motion problems generally have two basic steps:
1. Identify all of the forces acting on an object.
2. Use Newton’s laws and kinematics to determine the motion.
Understanding the first step is the primary goal of this chapter. We’ll turn our attention to step 2 in the next section.
A typical physics problem describes an object that is being pushed and pulled in various directions. Some forces are given explicitly, while others are only implied. In order to proceed, it is necessary to determine all the forces that act on the object. It is also necessary to avoid including forces that do not really exist. Now that you have learned the properties of forces and seen a catalog of typical forces, we can develop a step-by-step method for identifying each force in a problem. A summary of the most common forces we’ll come across in the next few chapters.

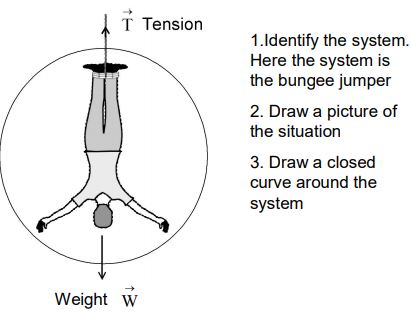
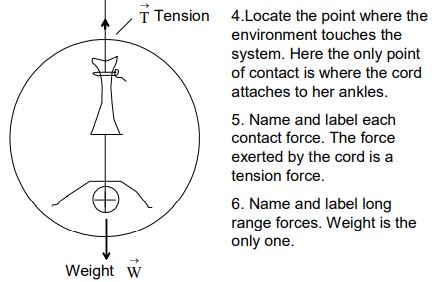
1. Identify “the system” and “the environment”. The system is the object whose motion you wish to study; the environment is everything else.
2. Draw a picture of the situation. Show the object-the system-and everything in the environment that touches the system. Ropes, springs, and surfaces are all parts of the environment.
3. Draw a closed curve around the system. Only the object is inside the curve; everything else is outside.
4. Locate every point on the boundary of this curve where the environment touches the system. These are the points where the environment exerts contact forces on the object.

5. Name and label each contact force acting on the object. There is at least one force at each point of contact; there may be more than one. When necessary, use subscripts to distinguish forces of the same type.
6. Name and label each long-range force acting on the object. For now the only long-range force is weight.
Example: Identifying forces on a bungee jumper:
A bungee jumper has leapt off a bridge and is nearing the bottom of her fall. What forces are being exerted on the bungee jumper?

Free-Body Diagrams
Having discussed at length what is and is not a force, and what forces do to an object, we are ready to assemble our knowledge about force and motion into a single diagram called a free-body diagram. A free-body diagram represents the object as a particle and shows all of the
forces acting on the object. Now that we have forces to consider, we expand our visual overview to include force identification and a free-body diagram. Learning how to draw a correct free-body diagram is a very important skill, in further section of NLM FBD will become a critical part of our strategy for solving motion problems. For now, let’s concentrate on the basic skill of constructing a correct free-body diagram.

Drawing a free body diagram
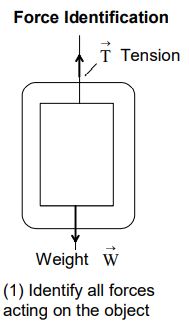
1. Identify all forces acting on the object.
2. Draw a coordinate system. Use the axes defined in your pictorial representation. If those axes are tilled, for motion along an incline, then the axes of the free-body diagram should be similarly tilted.
3. Represent the object as a dot at the origin of the coordinate axes. This is the particle model.
4. Draw and label the net force vector ${\overrightarrow{F}}_{\text{net }}$.Draw this vector beside the diagram, not on the particle. Or, if appropriate, write ${\overrightarrow{F}}_{\text{net }}=\overrightarrow{0}$. Then check that ${\overrightarrow{F}}_{\text{net }}$points in the same direction as the acceleration vector  $\overrightarrow{a}$on your motion diagram.

Examples: a book lying on a horizontal surface.

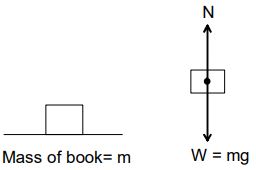
A free body diagram of the book alone would consist of its weight (W = mg) acting through the centre of gravity and the reaction (N) exerted on the book by the surface.
Examples: Forces on an upward-accelerating elevator An elevator, suspended by a cable, speeds up as it moves upward from the ground floor. Draw a free-body diagram of the elevator.

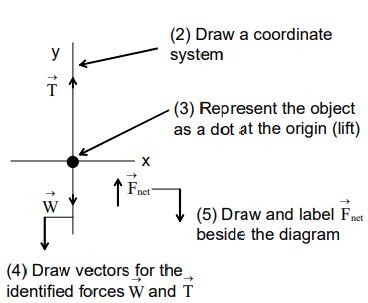
The coordinate axes, with a vertical y-axis, are the ones we would use in a pictorial representation of the motion.
The elevator is accelerating upward, so ${\overrightarrow{F}}_{\text{net }}$must point upward. For this to be true, the magnitude of $\overrightarrow{T}$ must be larger than the magnitude of $\overrightarrow{w}$. The diagram has been
drawn accordingly.
Examples: For inclined plane

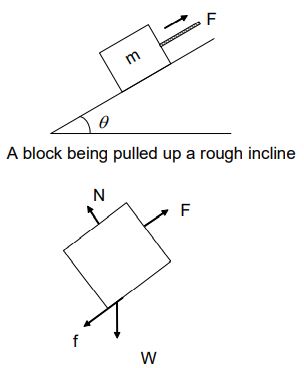
Identifying forces for interacting objects
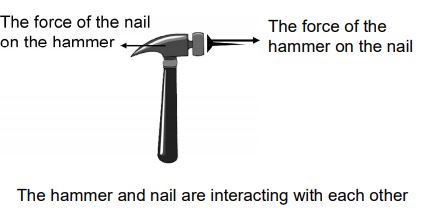
Think about the hammer and nail in Figure. The hammer certainly exerts a force on the nail as it drives the nail forward. At the same time, the nail exerts a force on the hammer. If you are not sure that it does, imagine hitting the nail with a glass hammer. It’s the force of the nail on the hammer that would cause the glass to shatter.

Indeed, if you stop to think about it, any time that object A pushes or pulls on object B, object B pushes or pulls back on object A. As sumo wrestler A pushes on sumo wrestler B, B pushes back on A. (If A pushed forward without B pushing back, A would fall over in the same way you do if someone suddenly opens a door you’re leaning against.) Your chair pushes upward on you (a normal force) while, at the same time, you push down on the chair. These are examples of what we call an interaction. An interaction is the mutual influence of
two objects on each other.
These examples illustrate a key aspect of interactions:
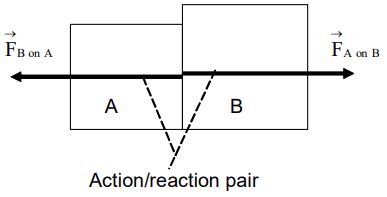
The forces involved in an interaction between two objects always occur as a pair. To be more specific, if object A exerts a force ${\overrightarrow{F}}_{\mathrm{A}\text{ on }\mathrm{B}}$ on object B, then object B exerts a force ${\overrightarrow{F}}_{\mathrm{B}\text{ on }\mathrm{A}}$ on object A. This pair of forces, shown in Figure, is called as action/reaction pair.

Reasoning with Newton’s Third Law
We’ve discovered that two objects always interact via an action/reaction pair of forces. Newton was the first to recognize how the two members of an action/reaction pair of forces are related to each other. Today we know this as Newton’s third law:
Newton’s third law: Every force occurs as one member of an action/reaction pair of forces.
The two members of an action/reaction pair act on two different objects.
The two members of an action/reaction pair point in opposite directions, and are equal in magnitude. 
Each force in the action/reaction pair acts on a different objects :

Example: In order to understand the motion of a single object subject to external forces, we took the object to be the system and everything else to be the environment.
Now we’re interested in the motion of two or more objects that interact with each other, so we’ll expand our system to include all these interacting objects. For example, for a truck pushing a car, we would take the car and truck together as the system, while the road and the earth would make up the environment, as shown in Figure.

$\begin{array}{l}{\overrightarrow{\mathrm{F}}}_{12}=\text{ force on car by truck }\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\overrightarrow{\mathrm{W}}}_{\text{truck }}=\text{ weight of the truck }\\ {\overrightarrow{\mathrm{F}}}_{21}=\text{ force on truck by car }\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\overrightarrow{\mathrm{W}}}_{\mathrm{car}}=\text{ weight of the }\mathrm{car}\end{array}$

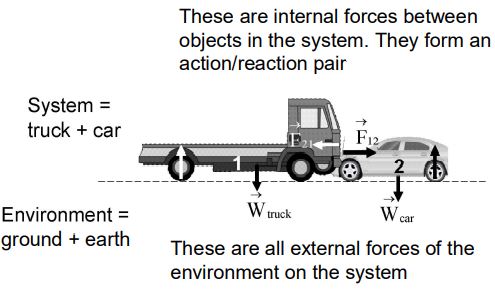
With the system chosen in this way, we can make a distinction between two classes of forces, again shown in Figure External forces are forces on objects in the system that originate from outside the system; that is, they are forces of the environment on the system. For example, the weight forces of the car and truck are external forces because they are the forces of the earth (part of the environment) on the vehicles. Internal forces, on the other hand, are forces between objects in the system. The force that the truck exerts on the car is an internal force between the two objects in this system.
Normally any problem relating to Newton’s laws is solved in following four steps:
Step 1: Decide the system
First of all we decide the system on which the laws of motion are to be applied. The system may be a single particle, a block or a combination of two or more blocks, two blocks connected by a string, etc. The only restriction is that all parts of the system should have the same acceleration.

Step 2: Identify the forces
Once the system is decided, we make the list of all the forces acting on the system. Any force applied by the system on other bodies is not included in the list of the forces.
Step 3: Make a free body diagram (FBD)
Then we make a free body diagram of the system and indicate the magnitude and direction of all the forces listed in step 2 in this diagram.
Step 4: Choose axes and write equations
i) In the last step we choose any two mutually perpendicular axes say x and y in the plane of the forces in case of coplanar forces.
ii) Choose the x-axis along the direction in which the system is known to have or is likely to have the acceleration.
iii) A direction perpendicular to it may be chosen as the y–axis. If the system is in equilibrium, any mutually perpendicular directions may be chosen.
iv) Write the components of all the forces along the x – axis and equate their sum to the product of the mass of the system and its acceleration, i.e., 

This gives us one equation
v) Now, we write the components of the force along the y – axis and equate the sum to zero. This gives us another equation, i.e., $\sum {\mathrm{F}}_{\mathrm{y}}=0$  ……………. (2)
Note:
i) If the system is in equilibrium we will write the two equations as: $\sum {\mathrm{F}}_{\mathrm{x}}=0\text{ and }\sum {\mathrm{F}}_{\mathrm{y}}=0$ii) If the forces are collinear, the second equation, i.e., $\sum {\mathrm{F}}_{\mathrm{y}}=0$ is not needed.

2.13. MOTION OF BODIES IN CONTACT FORCE OF CONTACT
Let us consider the case of two bodies of masses $m_1 and m_2$ in contact placed on a frictionless surface as shown in the figure.
Our aim is to calculate the acceleration produced and the force of contact between the bodies.

$a=\frac{\text{ force }}{\text{ Total mass }}=\frac{F}{m_1+m_2} ...........\left(1\right)$

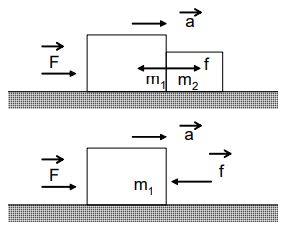
The free body diagram of mass m1 is also shown in fig.
We have $\mathrm{F}-\mathrm{f}={\mathrm{m}}_1\mathrm{a}$

$\text{ or }f=\mathrm{F}-{\mathrm{m}}_1\mathrm{a}=\mathrm{F}-\frac{{\mathrm{m}}_1\times \mathrm{F}}{{\mathrm{m}}_1+{\mathrm{m}}_2} .......\left(2\right)$

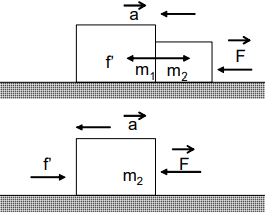
When the force is applied on the body of mass $m_2$ as shown in fig. then we have

$\text{ Acceleration }=\frac{\mathrm{F}}{{\mathrm{m}}_1+{\mathrm{m}}_2}$

The free body diagram of the body of mass $m_2$is also shown in the fig.

Now we have $F=f‘=m_{2}a$ $\text{ or }{f}^{\mathrm{\prime }}=f^{\mathrm{\prime }}-m_{2}a=F-\frac{m_{2}F}{m_1+m_2}$

Motion of Connected Bodies
Let us consider the case of two bodies of masses $m_{1 }and m_2$ connected by a thread and placed n a smooth horizontal surface as shown fig. A force F is applied on the body of mass $m_2$in forward direction as shown. Our aim is to consider the acceleration of the system and the tension T in the thread. The forces acting separately on two bodies are also shown in the figure.

$\begin{array}{r}\text{ From fig. }\mathrm{T}={\mathrm{m}}_1\mathrm{a} ......\left(1\right)\\ \mathrm{F}-\mathrm{T}={\mathrm{m}}_2\mathrm{a}........\left(2\right)\end{array}$

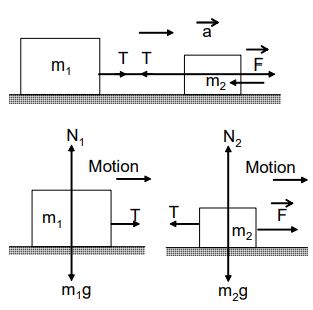
Adding (1) and (2)

$\mathrm{F}=\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)\mathrm{a} \mathrm{or} \mathrm{a}=\frac{\mathrm{F}}{{\mathrm{m}}_1+{\mathrm{m}}_2}$ …….(3)

The acceleration of the system can be calculated from equation (3) and tension in thread by equation (1)