1.1 INTRODUCTION
A table can be moved from one place to another by either pushing it or pulling it
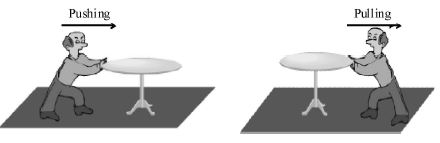
Similarly, you can open a door by either pushing or pulling it. When a ball is thrown with more force, it travels a
longer distance. The shape of a bottle can change when it is squeezed. Also, the direction of a moving ball can
change by striking it.
Have you wondered how the shape of a bottle changes when squeezed? Or how can the direction of a moving ball change by kicking it in different ways?
All the above activities can be associated with pushing or pulling.
Therefore, whenever an object is moved, we can say that it has either been pushed or pulled. This push or pull is known as force. In other words, a body moves whenever a force is applied to it. Therefore, a body cannot move unless a force is applied. Apart from push or pull, force is any action that has the tendency to change the position,
shape, or size of an object. Everyday actions such as pushing, pulling, stretching, lifting, squeezing, and twisting are also examples of force. Let us try to list some examples of everyday force and see if we can classify them as push or pull.
Examples
1. Hitting a cricket ball with a bat
2. Opening a door
3. Plucking a flower
4. Flying a kite
5. Moving a wheel barrow
6. Hitting a tennis ball with a racquet
7. Taking a carrot out of the ground
8. Playing on a swing
9. Picking up a shopping bag
10. Squeezing a toothpaste tube
1.2 INTERACTION BETWEEN FORCES
Have you ever seen an arm wrestling match?
In an arm wrestling match, both the players try to push each other’s hand towards the table. Hands move along the direction of the player who applies a greater force. The player who is able to apply more force wins the match.
A table in your room or a vehicle parked outside your house cannot move unless it is either pushed or pulled. To move a table, you have to either push or pull it.
In cricket, a bat exerts force on the ball. Thus, the ball is able to gain speed and can reach the boundary line. Thus, we can observe that force comes into play when at least two bodies interact with each other. Can you list the two interacting bodies in the cases that we have discussed?
|
Scenario |
Interacting bodies |
|
Arm wrestling Arms of the players Pushing or pulling a table A moving vehicle Bat hitting a ball |
Arms of the players You and the table Vehicle and the road (or the ground) Bat and ball |
1.3 EFFECTS OF FORCE
Force cannot be seen, heard, or tasted. Only its effects can be felt or seen. The various effects of force are:
1. It can move a body initially at rest.
2. It can bring a moving body to rest.
3. It can change the direction of a moving body.
4. It can change the speed of a moving body.
5. It can change the shape of a body.
6. It can change the size of a body.
Let us take an example of a football lying in a field (fig – A). When a player hits the ball, it starts moving, i.e., it starts moving only when we apply force. Thus, force can move a body initially at rest.
Now, if the goalkeeper catches the moving ball (fig – B), then it comes to rest. The goalkeeper applies a force to stop the moving ball. Hence, we can say that force can bring a moving body to rest.
If another player kicks the moving ball in the opposite direction (fig – C), then it starts moving in the direction
towards which it is kicked i.e. the direction of the football changes. The player applies force on the football to change its direction. Hence, force can change the direction of a moving body. Also, if the player hits the ball hard, then the net speed of the ball will also change. Hence, the speed of a moving body can be changed by applying force.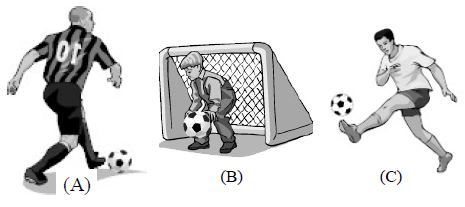
The shape of a deflated football can be changed by inflating it. When you inflate a football, you apply force on the pump. Hence, force can change the shape of an object. Also, if you keep inflating the football, then its size will keep on increasing. Hence, force can change the size of an object.
1.4 CONTACT FORCES
Ramu is cycling on the road. He observes that as he stops pedaling, the cycle stops moving after traveling for some distance. Let us see why this happens?
Forces acting between two bodies can be classified into two broad categories: Contact force and non-contact force.
Contact forces are those that act between two objects, which are in direct contact with each other.The two common examples of contact forces are muscular and frictional.
I. Frictional Force
Earlier you had seen that as Ramu stops pedaling the bicycle, it stops after some time. This happens due to the
external force acting between the road and tyres of the bicycle. This force is known as the frictional force. The force of friction acts between all moving bodies, which are in contact with one another. The force of friction always acts opposite to the direction of motion. The magnitude of this force depends on the nature of the surface in contact.
NOTE
1. Frictional force is a contact force.
2. Frictional force always acts between two moving objects, which are in contact with one another.
3. Frictional force always acts opposite to the direction of motion.
4. Frictional force depends on the nature of the surface in contact.
II. Muscular Force
The force applied by the action of muscles in our body is termed as muscular force.
For example, when you pick up a book placed on the table using your hands, you apply muscular force. For lifting the book from the table using your hands, you had to touch the book. You cannot lift the book without making contact with it. Hence, muscular force is a contact force.
Like humans, animals also use muscular force to perform various activities. For example, birds fly in the air by
flapping their wings.
1.5 NON CONTACT FORCES
Does force act only when two objects are in contact?
To understand, let us perform a small activity. Take a bar magnet and an iron nail. Bring the magnet close to the iron nail, but do not bring them in contact.
What do you observe?
The iron nail moves towards the magnet. This means that there must be a force that is acting between the magnet and the iron nail.
Since the iron piece moves towards the magnet (even when they are not in contact), we can say that the force exerted by the magnet on the iron piece is a non-contact force.
I. Magnetic force
Non-contact forces are those forces that act between two objects, but are not in direct contact with each another.
Examples of non-contact forces include magnetic force, electrostatic force, and gravitational force.
What will happen if you bring the South Pole of a bar magnet close to the North Pole of another bar magnet?
1.5 NON CONTACT FORCES
Does force act only when two objects are in contact?
To understand, let us perform a small activity. Take a bar magnet and an iron nail. Bring the magnet close to the iron nail, but do not bring them in contact.
What do you observe?
The iron nail moves towards the magnet. This means that there must be a force that is acting between the magnet and the iron nail.
Since the iron piece moves towards the magnet (even when they are not in contact), we can say that the force exerted by the magnet on the iron piece is a non-contact force.
I. Magnetic force
Non-contact forces are those forces that act between two objects, but are not in direct contact with each another.
Examples of non-contact forces include magnetic force, electrostatic force, and gravitational force.
What will happen if you bring the South Pole of a bar magnet close to the North Pole of another bar magnet?![]()
The magnets will attract each other. They attract each other with magnetic force.
What will happen if you bring the North Pole of both bar magnets close to each other?![]()
The bar magnets will repel each other. The force with which they repel each other is known as magnetic force.
NOTE
1. Magnetic force can be attractive as well as repulsive.
2. Magnetic force is a non-contact force.
3. Magnetic force acts between two magnets, or between a magnet and a magnetic material (such as iron).
4. Magnetic force depends on the strength of the magnet used.
5. Magnetic force also depends on the distance between the interacting bodies.
II. Electrostatic force
Take a paper and tear it into pieces. Now, rub a plastic scale against dry hair and bring this scale close to the paper pieces. What do you observe?
You will observe that the pieces of paper are attracted towards the scale. This happens because rubbing of the scale against dry hair produces an electrostatic charge. Thus, the scale attracts the pieces of paper by a non-contact force known as electrostatic force.
NOTE
1. Electrostatic force is a non-contact force.
2. Electrostatic force can be attractive as well as repulsive.
3. Electrostatic force is the force that exists either between two charged bodies, or between a charged and uncharged body.
4. Electrostatic force depends on the magnitude of charge present in the bodies.
5. Electrostatic force also depends on the distance between the interacting bodies.
III. Gravitational force
Do you know why apples fall towards the ground from trees? Why does water from a tap flow down?
The Earth attracts everything (that is near or on its surface) towards its centre by a noncontact force known as gravitational force. It is this force that makes an apple fall towards the ground from the tree and makes the water from a tap flow down.
NOTE
1. Gravitational force is a non-contact force.
2. Gravitational force is an attractive force.
3. Gravitational force is the force that is exerted by the earth on every object, which is near or on its surface.
4. Gravitational force depends on the mass of the body.
5. Gravitational force also depends on the distance between the Earth and body.
1.6 ACCELERATION
To develop the idea of acceleration, let us consider a body moving in a straight line with a non-uniform velocity. For example, let a train start from rest at station A. When it starts moving, its velocity increases and after a certain time interval it attains a constant velocity. As the next station approaches, its velocity gradually decreases and finally become zero at the station B.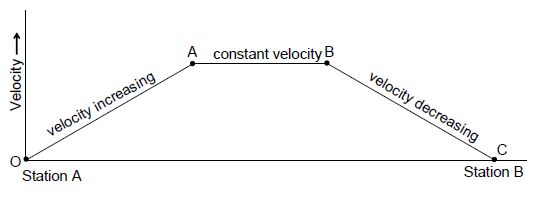
These changes in the velocity of a moving body are described in terms of acceleration. Acceleration is denoted by a, and is defined as follows:
The change in the velocity of a body per unit time is called acceleration.
Acceleration =
If, Velocity of a body at and, Velocity of a body at
Then, Change in velocity =
and, Time interval =
As per definition, the acceleration of the body over the time interval to is given by,
The acceleration given by the above equation is actually the average acceleration over the time interval to .
However, if the time interval is very small, then acceleration obtained is called acceleration at time .
The rate of change of velocity of a body is called its acceleration. The change in the velocity may be due to a change in its speed or direction of motion or both.
But when a body moves in a straight line, its direction does not change. So, for bodies travelling along a straight line, the acceleration is due to the change in its speed during its motion. However, when a body moves along a circular path at a constant speed, the acceleration in the body is due to the change in its direction. These aspects shall be discussed in detail in higher classes.
Acceleration of a body in terms of its initial and final velocities
Acceleration =
Where:
u = Initial velocity of the body
v = Final velocity of the body
t = Time interval
a = Acceleration of the body
Units of acceleration. Acceleration is given by,
The SI unit of acceleration is, .
Some other (non-SI) units of acceleration which are used often are, centimetre per second squared, or cm
kilometre per hour squared, km/ or km
Positive Acceleration
Acceleration is described by the equation,
Acceleration,
If the final velocity of a moving body is greater
than the initial velocity, i.e., v > u, then
Acceleration,
= A positive quantity
Thus, the acceleration of a moving body is positive if its final velocity is greater than the initial velocity. In other
words, when the velocity of a body increases with time, its acceleration is positive. In common practice, positive
acceleration is simply called acceleration.
Example: A body dropped from a certain height gains velocity as it falls down towards the earth. So, a body falling towards the earth has positive acceleration.
Note: Acceleration is taken to be positive if it acts in the direction of velocity, and negative when in the direction
opposite to the direction of velocity.
Negative Acceleration (or retardation)
We know, Acceleration,
If the final velocity of a moving body is less than the initial velocity , i.e., v < u, then
Acceleration,
Thus, the acceleration of a moving body is negative when its final velocity is less than the initial velocity. In other
words, when the velocity of a body decreases with time, its acceleration is negative.
Example: When a ball (or stone) is thrown vertically upwards, its velocity decreases with time. So, the acceleration of a ball thrown vertically upwards is negative.
The velocity of a ball rolling on the floor keeps on decreasing until it stops. So, the acceleration of a ball rolling on the floor is negative.
Negative acceleration is also called deceleration or retardation.
So, when the velocity of a body decreases with time, it is said to be under retardation.
For a body undergoing retardation, the final velocity is less than initial velocity. Thus, retardation is actually acceleration with a negative sign. For example, if a body has an acceleration of – 5 m/, then the retardation of the body is +5 m/
Units of Retardation
Retardation (or negative acceleration) has the same units as acceleration. Thus, the SI unit of retardation is metre per second squared (m/ or )
What is meant by uniform acceleration?
When a moving body has the same acceleration throughout its motion, it is said to have uniform acceleration. The
uniform acceleration is also called constant acceleration.
Acceleration is defined as the rate of change of velocity. So, uniform acceleration may be defined as follows:
When a body travels in a straight line and its velocity changes by equal amounts in equal intervals of time, it is said to have a uniform acceleration.
The motion of a body with uniform acceleration is called uniformly accelerated motion.
Examples
a) A body falling freely under gravity has uniform acceleration.
b) A ball moving down an inclined plane has uniform acceleration.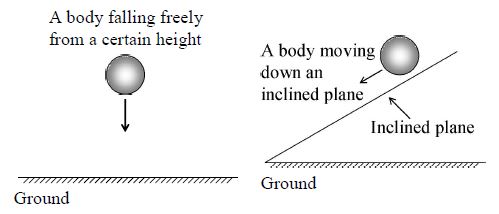
Non-Uniform Acceleration
Non-uniform acceleration is also called variable acceleration. When a moving body has different accelerations at
different points of time during its motion, it is said to have non-uniform acceleration, or variable acceleration.
Acceleration is defined as the rate of change of velocity. So, the non-uniform acceleration may be defined as follows:
When the velocity of a body changes by unequal amounts in equal intervals of time, it is said to have a non-uniform acceleration.
Example: An auto/car driven on a crowded city-road with frequent application of brakes has a non-uniform acceleration.
1.7 CALCULATION OF FORCE
Consider a body of mass ‘m’ acted upon by a force ‘F’ to produce an acceleration ‘a’ . Then mathematically, force is
defined as the product of mass and acceleration.
Force = Mass × Acceleration
F = m × a = ma
(or) F = ma =
Units of Force
S.I unit of force = kg m/ = newton
C.G.S unit of force = g cm/ = dyne.
Note :
i) 1 newton is that much force which produces an acceleration of 1 m/ in a body of mass 1 kg.
ii) The force is said to be 1 dyne if it produces 1 cm/ acceleration in a body of 1g mass.
Relation between newton and dyne
1 newton (N) = 1 kg m/s2 = 1000 g × 100 cm/s2
= 100000 g cm/s2 = 105 gcm/s2 = 105 dyne
1.8 FREE FALL
The motion of a body towards the earth when no other force except the force of gravity acts on it is called a free fall.
Thus all the freely falling bodies, lighter or heavier, fall towards the earth with the same acceleration.
According to Galileo Galilei, if there were no air, all the bodies having different masses when dropped simultaneously from the same height would hit the ground at the same time.
Later Robert Boyle proved this experimentally. He placed a coin and a feather in a long glass tube and removed its air with the help of vacuum pump. When the tube was inverted both the coin and the feather fell to the bottom of the tube at the same time. Thus the acceleration produced in all the freely falling bodies is the same, and does not depend upon the mass of the falling body.
1.9 ACCELERATION DUE TO GRAVITY
The earth attracts every other body lying near or on its surface towards its centre. The origin of this force between the earth and a body is due to interaction between their masses.
The force of attraction exerted by the earth on a body is called gravitational pull or gravity.
We know that when force acts on a body, it produces acceleration. Therefore, a body under the effect of gravitational pull must accelerate.
The acceleration produced in the motion of a body under the effect of gravity is called acceleration due to gravity. It is denoted by g.
The value of acceleration due to gravity near the surface of the earth is 9.8ms–2.
The value of acceleration due to gravity does not depend upon, whether the body falling under gravity is a light one or a heavy one i.e., the value of g is independent of the mass of the body.
1.10 MASS AND WEIGHT
Mass
Quantity of matter possessed by a body, is called the mass of the body. It is represented by the symbol m. It is a scalar quantity.
Nature : A body with more mass, needs a greater effort (force) to move it from rest or stopping it from motion. The body exhibits inertia. Thus, mass offers inertia. This mass is called inertial mass (m1). A body never has a zero mass.
Measurement of mass :
Mass of a body is measured by a beam balance by comparing the mass with bodies of known mass. At one place, bodies of same mass have same pull of gravity on them.
A beam balance works on the principle of moments (Bodies of equal masses, having equal weights, have equal and
opposite moments about fulcrum of the balance, when suspended at equal distances from the fulcrum, and made the beam horizontal).
Weight
The force with which a body is attracted towards the centre of the earth, is called the weight of the body. It is represented by the symbol W.
It is a vector quantity having direction towards the centre of the earth.
Expression for weight
If mass of a body = m
Acceleration due to gravity of the earth = g
Then from relation , Force = Mass × Acceleration i.e., W = mg
Nature :
As W = mg, the weight of a body will vary from place to place due to variation in value of g. A body has zero weight at the centre of the earth (where g = 0). On the surface of earth, the value of g is 9.8 m/s2.
g value at poles is greater than at equator.
Measurement of weight :
Weight of a body is measured by a spring balance.
Difference between Mass and Weight
|
Mass |
Weight |
|
Mass is quantity of matter possessed by a body |
Weight is the force with which a body is attracted towards the centre of the earth. |
|
It is a scalar quantity. |
It is a vector quantity. |
|
Its SI units is kilogram (kg.) |
Its SI unit is newton (N). |
|
Mass of a body remains constant at all places |
Weight of the body changes from place to place. |
|
Mass of a body is never zero. |
Weight of a body becomes zero at the centre of the earth. |
|
Mass is measured by a beam balance. |
Weight is measured by a spring balance. |
1.11 NEWTON’S FIRST LAW OF MOTION
Let us suppose that a book is lying on a table. It is at rest. Can the book change its position by itself?
Obviously, no.
The book will not move by itself, unless you push or pull or lift it. Thus, the position of the book can change its position, only when some force is applied.
A person riding a bicycle along a level road does not come to rest immediately after he stops pedaling, unless he applies the brakes. Here, on applying the brakes, the state of motion is changed to a state of rest.
These examples contribute to Newton’s First law of motion.
A body continues to be in the state of rest or of uniform motion along a straight line unless it is compelled by an external force to change its state.
“Objects keep on doing what they are doing, unless they are acted upon by an unbalanced force”.
The of Newton’s First law of motion introduces the concept of inertia and defines force.
Therefore the first law of motion is also known as the law of inertia.
1.12 INERTIA
From Newton’s first law of motion, it is clear that a body is unable to change its state of rest or motion by itself. This property of the body is known as inertia.
Inertia of a body may be defined as the tendency of a body to oppose any change in its state of rest or uniform motion.
For example, a book lying on a table will remain where it is placed unless it is displaced. Similarly, a ball rolling on a horizontal surface keeps on rolling unless the force of friction between the ball and the surface stops it.
Mass and inertia : Inertia is an inherent property of each body by virtue of which it has a tendency to resist the
change in its state of rest or state of uniform motion. The property of inertia is due to the mass of a body. The greater the mass, the greater is the inertia of a body.
For example, if a body has a mass of 1kg and another body has a mass of 20 kg, then the body having 20 kg mass will have more inertia since its mass is more.
Types of inertia
Inertia can be divided into three types.
i) Inertia of rest
ii) Inertia of motion
iii) Inertia of direction
Inertia of rest : The tendency of a body by virtue of which it cannot change its state of rest by itself is called inertia of rest.
Examples:
i) A person in a car tends to fall backward when the car starts suddenly : When a person is sitting or standing in a stationary car, both the car and the person are at rest. When the car starts suddenly, the lower part of the person’s body starts moving forward with the car . But the upper part of the body tends to remain in the state of rest due to inertia of rest. As a result, he falls backward.
ii) On shaking or giving jerks to the branches of a tree, the fruits fall down : Initially both the tree and the fruits hanging to its branches are in a state of rest. When the branches of the tree are shaken, it is set into motion while the fruits remain in a state of rest due to the inertia of rest. Thus, the fruits get detached from the branches and fall down due to the pull of gravity.
iii) The carpet is beaten with a stick to remove the dust particles : When the carpet is beaten with a stick, the fibres of the carpet come in motion and hence move forward. On the other hand, the dust particles remain at rest due to inertia of rest. Therefore, they fall down.
Inertia of motion : The tendency of a body by virtue of which it cannot change its state of motion by itself is called inertia of motion.
Examples:
i) A person in a moving car tends to fall forwardwhen the car stops suddenly: When a person is sitting or standing in a moving car, both the car and the person are in the state of uniform motion. When the car stops suddenly, the lower part of the person’s body comes to rest along with the car. The upper part of his body tends to remain in the state of motion due to its inertia of motion. As a result, the person leans forward.
ii) A girl jumping out of a speeding van may fall forward: This is because as the foot of the girl touches the ground, the lower part of her body comes to rest while the upper part of his body remains in motion due to inertia of motion.
iii) A cyclist does not come to rest immediately after she stops pedaling: A cyclist riding along a road does not come to rest immediately after she stops pedaling. The bicycle continues to move forward due to the inertia of motion.
iv) When a rotating fan is switched off it continues to rotate due to inertia of motion.
Inertia of direction : The tendency of a body to oppose any change in its direction of motion by itself is known
as inertia of direction.
Examples:
i) When a fast-moving bus negotiates a curve on the road, passengers fall towards the centre of the curved road.
This is due to the tendency of the passengers to continue to move in a straight line.
ii) A stone tied to a string and whirled along a circular path flies off tangentially due to inertia of direction, if the
string breaks.
iii) While sharpening a knife, sparks fly off tangentially from the grinding stone, due to inertia of direction.
iv) Mud sticking to a cycle tyre flies off tangentially. That is why mud-guards are provided on the front and rear
wheels of the cycle.
1.13 LINEAR MOMENTUM
Consider two balls A and B. Let ball A be heavier than ball B. i.e. mass (m1) of ball A is greater than the mass (m2) of the ball B. Suppose both balls are moving with same velocity . The force required to stop ball A is more than the force required to stop ball B. This shows that the heavier ball has more quantity of motion than the lighter ball. Thus, the quantity of motion of a body is directly proportional to the mass of the body.
Now consider two balls of same mass moving with different velocities. The force required to stop the fast- moving
ball is more than the force required to stop the slow-moving ball. So the quantity of motion of the body is directly
proportional to the velocity of the ball.
Conclusion: The quantity of motion of the moving body is proportional to
i) mass of the body
ii) velocity of the body.
This quantity of motion possessed by a moving body is known as momentum of the body (or) the total quantity of
motion contained in a body is called momentum.
Mathematical expression: Momentum of a body is equal to the product of the mass (m) of the body and the velocity
of the body. It is denoted by .
Note :
i) Momentum is a vector quantity.
ii) The direction of momentum of a body is same as that of the direction of the velocity of the body.
iii) The SI and CGS units of momentum are kg-m/s and gm-cm/s respectively.
1.14 NEWTON’S SECOND LAW OF MOTION
Newton’s second law gives the quantitative definition of force. In other words, it measures force.
According to Newton, when force is applied upon a body, then acceleration is produced.
The acceleration produced in a body is
a) directly proportional to the force acting on it
i.e. a f ________ (i)
b) inversely proportional to the mass of the body
i.e. __________ (ii)
from (i) and (ii) we have
________ (iii)
Where k is constant.
Now if F = 1 unit of force
m = 1 unit of mass and
a = 1 unit of acceleration then k = 1
and hence F = ma ________ (iv)
So, Force acting on the body = mass of the body × acceleration produced in the body
Newton’s second law states that: “The magnitude of the resultant force acting on a body is proportional to the
product of the mass of the body and its acceleration. The direction of the force is the same as that of the acceleration”.
Newton’s second Law in terms of momentum
The rate of change of momentum of an object is proportional to the net force applied on the object. The direction of the change of momentum is the same as the direction of the net force.
Derivation F = ma
Consider a body of mass m moving with initial velocity u. Let a force F act on the body for time t so that the velocity of the body after time t is v.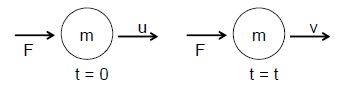
Initial momentum of the body () = m u
Final momentum of the body () = m v
Now, change in momentum of the body
= = mv – mu = m (v – u)
Time taken for this change in momentum
= (t – 0) = t
Rate of change of momentum
Note : Newton’s first law of motion is a special case of Newton’s second law of motion
We know that
If velocity of the body is constant i.e. u = v, then
Thus, no force is required to move a body with constant velocity or uniform velocity. If u = 0, then v is also zero; it
means the body will remain at rest if no external force is applied on the body. This is the first law of motion.
Units of Force :
S.I unit of force = kg m/s2 = newton
C.G.S unit of force = g cm/s2 = dyne.
Note :
i) 1 newton is that much force which produces an acceleration of 1 m/s2 in a body of mass 1 kg.
ii) The force is said to be 1 dyne if it produces 1 cm/s2 acceleration in a body of 1g mass.
Relation between newton and dyne :
1 newton (N) = 1 kg m/s2 = 1000 g × 100 cm/s2
= 100000 g cm/s2 = 105 gcm/s2 = 105 dyne
Acceleration Due To Gravity
The earth attracts every other body lying near or on its surface towards its centre. The origin of this force between the earth and a body is due to interaction between their masses.
The force of attraction exerted by the earth on a body is called gravitational pull or gravity.
We know that when force acts on a body, it produces acceleration. Therefore, a body under the effect of gravitational pull must accelerate.
The acceleration produced in the motion of a body under the effect of gravity is called acceleration due to gravity. It is denoted by g.
The value of acceleration due to gravity near the surface of the earth is 9.8ms-2.
The value of acceleration due to gravity does not depend upon, whether the body falling under gravity is a light one or a heavy one i.e., the value of g is independent of the mass of the body.
If ‘g’ is acceleration due to gravity, ‘m’ is the mass of a body; then the gravitational force on the body is ‘mg’ and is called the weight of the body.
weight = mass × acceleration due to gravity
i.e. W = mg.
Gravitational Units of force : Gravitational units of force is the force which produces an acceleration equal to the acceleration due to gravity in a unit mass.
a) Gravitational unit of force in S.I. system is kilogram weight or kilogram force.
1 kg wt = 1 kg × 9.8 m/s2 (on earth)
1 kg wt (kgf) = 9.8 kg m/s2 = 9.8 N (on earth)
b) Gravitational unit of force in C.G.S. system is 1 gram weight or gram force.
1 g wt = 1g × 980 cm/s2 (on earth)
1 g wt = 980 g cm /s2 = 980 dyne (on earth)
Some applications of Newton’s second law of motion
i) Lowering of hands while catching a ball
We know that force = rate of change of momentum
If a player does not lower his hands while catching the ball, the time to stop the ball is very little. So a powerful
force has to be applied to change the momentum of the ball. When a player lowers his hands, the time to stop the
ball is increased and hence less force has to be applied to cause the same change in the momentum of the ball.
Therefore, the hands of the player are not injured.
ii) Cement floor cause more injury than heap of sand: When a person falls on a cemented floor, the rate of change of momentum is very high because the person is abruptly stopped i.e. stopped in a very short interval of
time. Hence the person gets injured due to the application of a large force on his body due to the floor. On the
other hand, when a person falls on a heap of sand, the sand yields under the weight of the person. As a result of
this, the person comes to rest in a longer period of time. So the change in momentum takes place in longer
interval of time. Hence a small force is exerted on the body of the person when he falls on a heap of sand.
Therefore, he does not get injured.
iii) The use of seat belts in cars: These days all the cars are provided with seat belts for passengers to prevent
injuries in case of an accident. In a car accident, a fast running car stops suddenly. Due to this the car’s large
momentum is reduced to zero in a very short time. The stretchable seat belts worn by the passengers of the car
increase the time taken by the passengers to fall forward. Due to longer time, the rate of change of momentum of
passengers is reduced and hence less stopping force acts on them. So, the passengers may either not get injured
at all or may get less injuries. It is obvious that seat belts reduce the passengers’ momentum more gently and
hence prevent injuries.
1.15 NEWTON’S THIRD LAW OF MOTION
i) When a player kicks a football, the football moves forward and the foot of the player moves backward. The force with which the football is kicked by the foot of the player, is known as action. Due to this action force, the football moves forward. On the other hand, the force exerted by the football on the football on the foot of the player, is known as reaction. Due to this reaction force, the foot of the player moves backward.
ii) When a ball falls towards the earth, the earth exerts a force () on the ball, to attract the ball towards its centre. On the hand, the ball exerts a force () on the earth to move upward.
From these examples, we can conclude that, whenever two bodies collide with each other, they exert equal and opposite forces on each other. Out of these forces, one is known as action force and the other is known as reaction force.
The essence of this observation is tit for tat, also summarized as Newton’s 3rd law of motion.
From above examples, we can conclude that “whenever two bodies have influence on each other they exert equal and opposite forces on each other, out of these forces. One is known as action and other is known as reaction.
Newton’s Third law of motion – Statement
For every action, there is an equal and opposite reaction. That is, Action = – Reaction
Note : Action and reaction force are equal in magnitude but opposite in direction.
i.e. Action = – Reaction
In other words, whenever two bodies interact with each other, the force exerted by the first body on the second body (called action) is equal and opposite to that exerted by the second body on the first body (called reaction).
For example, a block when placed on the ground, exerts a force acting downwards equal to its weight W (mg) on the ground (due to the attraction by the earth). This is called action. The ground exerts an equal and opposite force W (mg) on the block in the upward direction. This is called reaction. From the above examples it is clear that,
Note:
i) Both action and reaction are forces [In this case, F = mg]
ii) Action and reaction act simultaneously, but act on different bodies. (In this case the block and the ground are two different bodies on which action and reaction act simultaneously)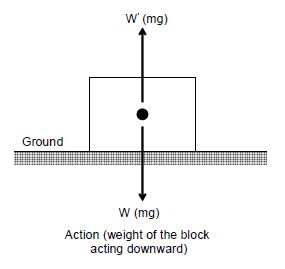
iii) Action and reaction act on different bodies. For this reason, they cannot cancel each other.
iv) Action and reaction forces occur in pairs only. (In this case if the block was not placed on the ground, there would be no reaction.)
Action and reaction are always equal and opposite
To show that action and reaction are equal and opposite, set up two similar spring balances as shown in the figure.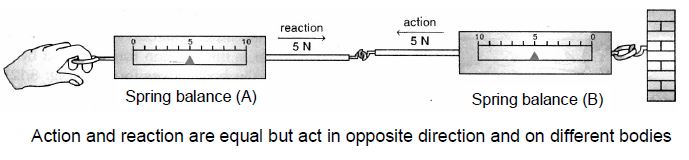
When spring balance A is pulled towards left, it exerts a force (say 5N) on the balance B. As a result, the spring
balance B reads 5 N (action). The balance A also reads 5 N. This means the balance B also exerts a force of 5 N on the balance A (reaction). Therefore, we see that action and reaction are equal but act in the opposite directions.
Examples of Newton’s third law of motion
i) Recoiling of a gun: When a gun is fired, the bullet goes out due to the force applied on it through the trigger (this is action). According to Newton’s third law of motion, the gun recoils backwards due to the reaction acting on it in the opposite direction. This gives a backward jerk to the shoulder of the gunman
ii) Flying of Jet plane and rocket: In jet engines and rockets, the fuel is burnt to produce a large quantity of hot gases. These hot gases come out of a nozzle (a fine opening) with a great force (this is action). According to
Newton’s third law of motion, the equal and opposite reaction pushes the jet aeroplane and rockets forward with
a great speed (this is reaction)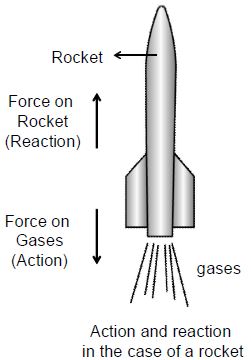
iii) Swimming : When a person swims, he pushes the water in the backward direction with his hands (this is action). As the reaction, the water pushes the person in the forward direction with an equal force.
iv) Walking: When we walk on the ground, our foot pushes the ground backwards (this is action). In return, the ground pushes our foot forward with an equal and opposite force, (this is reaction). The forward reaction
exerted by the ground on our foot makes us walk forward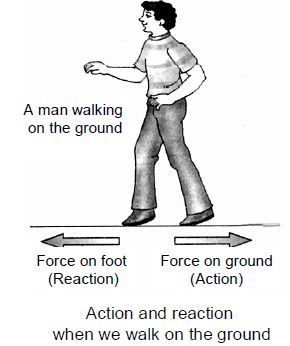
v) Rowing of a boat : When rowing a boat, the boatman pushes the water backwards with the oars (this is action). According to Newton’s third law of motion, the water exerts an equal and opposite push on the boat, which moves forward. (this is reaction). In fact, the harder the boatman pushes back the water with oars (i.e. the greater the action) the greater the reaction (force) exerted by the water and faster the boat moves forward.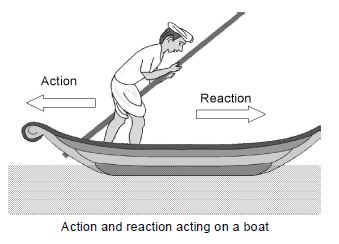
vi) Tying of a boat: The boatman ties his boat before allowing passengersto disembark, This is due to the fact that when the passengers start disembarking (getting out of the boat), they push the boat backwards with their feet (this is action). The boat exerts an equal and opposite force on the passengers in the forward direction which enables them to move forward (this is reaction). Since the boat is in the water, it moves backward due to the action (force) exerted by the passengers. So the boatman ties his boat to prevent the boat from sliding back in to the water.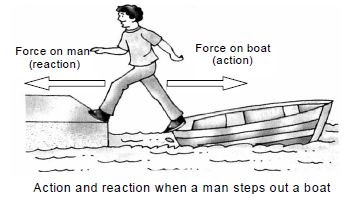
vii) Pain caused during hammering: We feel pain in our hand when we hammer a nail into a wooden plank, while hammering a nail, the force of the hammer on the nail is the action. According to Newton’s third law of motion the nail exerts an equal and opposite force on the hammer (the reaction). Since the hammer is held in our hand firmly, our hand experiences the force due to the reaction, and feels hurt.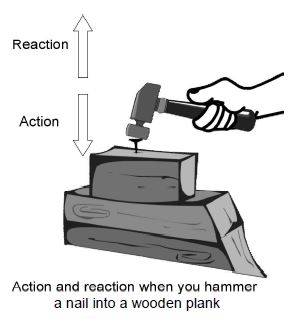
viii) Rebounding of a ball: When we strike a rubber ball against a hard floor, the ball exerts a force (called action) on the floor. According to Newton’s third law of motion, the floor exerts an equal and opposite force (called reaction) on the ball. The rubber ball, being light, rebounds.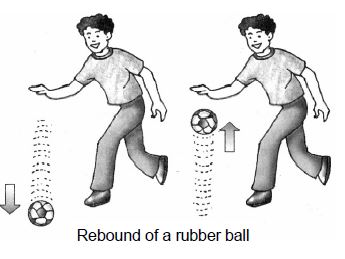
ix) Pushing a wall: When we exert a force on a wall by pushing the palm of our hand against it (this is action); then, according to Newton’s third law of motion, the wall exerts an equal and opposite force (called reaction) on our palm, and therefore we feel pain in our hand.
PRESSURE
1.16 INTRODUCTION
- Have you ever thought of these:
- How does a glider move in the air?
- Why a sudden outbreak of sand storm blew off the tops of the tents in desert.
- Why the paste comes out from the front end when it is pressed from the rear end?
- Why a camel moves faster than a horse in the desert?
- Why a sharp knife can cut easily in contrast to a blunt knife.
- How could we empty a cool drink bottle using a straw?
The answers for these questions can be answered from this topic.
1.17 THRUST
All bodies have a certain weight and a certain base area. When a body rests on a surface, it exerts a force equal to its weight, normal to its surface.
This force is called thrust.
Thrust is the total force or total weight acting normal to the surface.
Weight of the body is the product of mass and acceleration due to gravity
i.e., W = mg (where ‘g’ is acceleration due to gravity)
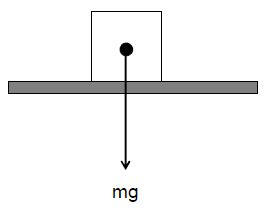
The value of acceleration due to gravity (g) is 9.8 ms-2 in S.I. system and 980 cm s2 in C.G.S. system. This is considered to be constant on the earth’s surface.
Units: Since thrust is defined as the total force or weight, its units are the same as force and weight.
|
Unit of thrust |
System of units |
Absolute units |
Gravitational units |
|
|
S.I |
Newton |
Kg.wt (or) kgf |
|
|
C.G.S. |
Dyne |
g.wt. (or) gf |
Kilogram weight (or) kilogram force
The weight of one kilogram object is called kilogram weight (or) the force exerted by one kilogram body on its
resting surface is called kilogram force. It is represented by kg wt (or) kgf.
Gram weight (or) Gram force
Weight of one gram object is called gram weight (or) the force exerted by one gram object on its resting surface is
called gram force. It is represented by g wt (or) gf respectively.
1.18 PRESSURE
Let us try understand the same from the following activity.
Try to fix a nail into the wall (i)with its tip pointing towards the wall (ii) with its head pointing towards the wall with same amount of force.
What do you observe?
In first case, the nail moves easily into the wall and in second case, it is almost impossible to fix the nail.
What is the reason for the above result?
In first case, thrust (force) applied is transmitted to the wall over a small area of contact and in second case thrust is transmitted to the wall over a large area of contact.
What can be concluded out of this?
The effect on the wall depends on both thrust and area of contact.
By changing either thrust or area of contact, the effect on the wall can be changed. This effect is called pressure.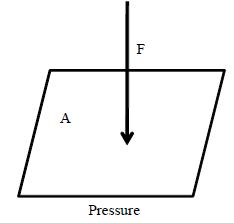
Units:
C.G.S. units: dyne/cm2 or g.wt/cm2
S.I. units: N/m2 or kg.wt/m2
Note:
i) The S.I. unit N/m2 is also known as Pascal. It is denoted by ‘Pa’.
ii) The other units of pressure are bar, torr, cm of Hg and mm of Hg.
iii) 1 atm = 105 Pascal = 105 N/m2
= 106 dyne /cm2 = 76 cm of Hg
= 760 mm of Hg = 760 torr
iv) Pressure on a body can be exerted from any direction. Hence, it has a no particular direction and is considered as a scalar quantity.
Applications of Pressure
i) Design of Wheels of different vehicles:
Depending on the requirement, wheels of different vehicles are designed accordingly. Two illustrations are cited here under:
Double wheel at rear end
In general, the weight (force) is more at the rear end of the trucks, buses etc.
This results in the development of greater pressure between the tyres and the road.
If the pressure is more, the rate of damage is more and it may lead to accidents.

Decreasing the force (weight) is practically not feasible, but the pressure can be decreased by increasing the area of contact between the tyres and the road.
This is done by using double tyres in the case of lorries and buses.
Broad chains for tankers
Army tankers are much heavier than the ordinary vehicles.
If they are provided with tyres, they cannot withstand the weight of the tanker and may result in the bursting of tyres.
In addition to this, the tankers have to move through deserts, forests and hill places.

To satisfy all these conditions and make the usage of tankers effective, wheels are designed with broad chains.
These broad chains occupy more area than the tyres, thereby exerting less pressure on the ground. This enables an easy movement.
This is done by using double tyres in the case of lorries and buses.
ii) Easy walking of camels in deserts
Animals like camels walk easily in deserts as compared to horses or donkeys because they have broad feet.
Broad feet exert less pressure on sandy ground.
iii) Usage of flat and long skies to slide: The skiers use flat and long skies to slide on the snow because the larger the area of cross-section, the less is the pressure on the snow.
Hence, a skier can easily slide over snow without sinking his feet in the ground.
It is for the same reason that sledges are never provided with wheels because the wheels increase pressure on snow.
iv) Sharpening of cutting edge of knives, blades and axes:
The cutting edge of knives, blades and axes are sharpened. As the cutting edge is sharpened, the area of contact
decreases and hence pressure exerted by it increases. Thus, they can easily penetrate a given surface.
v) Wide foundations for high-rise buildings:
Foundations of high-rise buildings are kept wide so that they exert less pressure on the ground and do not sink in due to the extremely high pressure of the building.
1.19 FLUID PRESSURE
A substance which can flow from one point to another is called fluid. Since liquids and gases can flow, so they are
known as fluids.
A fluid exerts three types of pressure
1. Downward Pressure
2. Upward Pressure
3. Lateral Pressure
1. Downward Pressure of Water: Consider a vessel (V) containing some water of weight (W), say 500 gm. wt. Let the area of its base (A) be 100 cm2. Then the weight of water (W) is the thrust acting on the base of area 100 cm2. This shows that liquids exert downward pressure.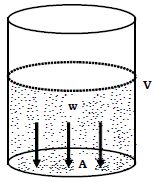
2. Lateral Pressure of Water: Take a long cylindrical vessel containing water and puch a hole (H) on its wall as shown in the given figure. The water comes out with a speed and falls at distance. This proves that liquid has lateral pressure.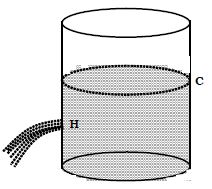
3. Upward Pressure of Water: Take a football and immerse it in water in a vessel (V) and leave it. The ball immediatly comes up and floats on water. This shows that water (or fluid) exerts pressure in the upward direction.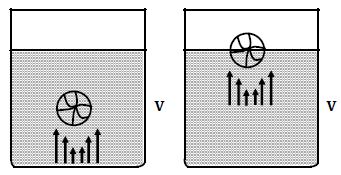
Hydrometer
A direct-reading instrument used for measuring the density or relative density of a liquid is called hydrometer.
Principle of hydrometer
(i) Hydrometer is based on the principle of floatation, i.e., the weight of the liquid displaced by the immersed portion of the hydrometer is equal to the weight of the hydrometer.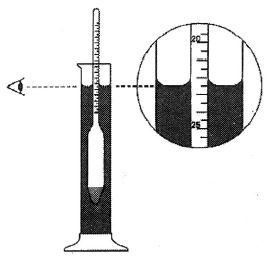
(ii) Hydrometer is a glass instrument. It consists of a cylindrical bulb having a spherical bulb at its lower end and a long stem (narrow tube) at its upper end.
The lower spherical bulb is partially filled with lead shots. This helps hydrometer to float (or stand) vertical in liquids. The stem has markings so that relative density of a liquid can be read off directly. The hydrometer is placed in the liquid taken in a glass jar. The reading against the level of liquid gives the relative density of the
liquid.
Mathematical Expression for Pressure in Fluids
Consider a beaker filled with a liquid of density d. Now imagine a cylindrical column of the liquid of height h and cross-sectional area A.
The force acting on the base of this imaginary cylindrical column of liquid is equal to the weight of the liquid contained in this column of liquid.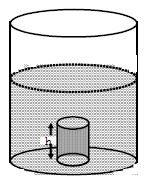
i.e, F = weight of liquid in cylindrical column of liquid F = mg —————- (1)
Now, mass of liquid in the cylinder column of liquid.
m = volume of cylindrical column × density of liquid = Area of cross section × length of cylindrical
column × density of liquid
m = A h d
weight of liquid in cylindrical column of liquid = mg = Ah d g
Putting this value in equation (1) we get F = Ah d g
pressure exerted by liquid at depth ‘h’
Does Fluid Pressure depend on Size, Shape and Area ?
You might be surprised to know that fluid pressure does not depend on size shape and area.
You have learnt earlier that pressure depends on area. This is true only in the case of solids.
But, when it comes to fluids (liquids and gases), the pressure exerted is independent of area. Let us understand it from the following activity.
Consider five containers A, B, C, D and E containing the same liquid of the same height from the bottom.
The shape, size and area of the containers are different from each other.
Do they exert the same (or) different pressure.
Let us check: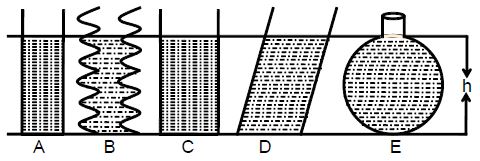
We know that the pressure exerted by the liquid depends on the height of the liquid, the density of the liquid and the acceleration due to gravity.
Pressure = height (depth) × density of liquid × acceleration due to gravity
Pressure = hdg
‘h’ is same in all the cases ( fluid level is same), ‘d’ is same in all the cases ( liquid is same) and ‘g’ is constant at a given place.
Thus, fluid pressure is the same in all the cases and it is independent of the shape, size and area of the container.
Liquids seek their own level
The apparatus in the figure above, shows five tubes of various shapes which are connected to each other by a horizontal pipe.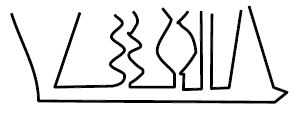
Fix the apparatus and pour water through any one of the vertical tubes.
It is observed that the level of the water is same in all the tubes though they have different shapes and areas of cross section.
Note: Fluids (Liquids and gases) move from a region of high pressure to that of low pressure.
Use: As we know water seeks its own level. When we open the tap, the water in the tap tries to maintain the same
level as the water in the tank.
But taps are kept below the level of the tank, so water comes out through the tap. Similarly, large water tanks are
constructed at a higher level and supplied to the locality.
1.20 PASCAL’S LAW
This law is also known as ‘the principle of transmission of fluid-pressure’.
This law states that ‘The pressure exerted at any point in an enclosed and incompressible liquid is transmitted equally in all 4 directions’.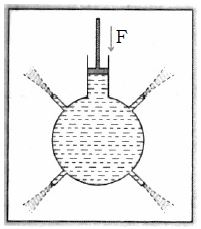
Example : Take a round bottom flask with a number of narrow openings on its sides, provided with an air-tight piston in its mouth. Fill it to the brim with water. Now push the piston down. Water will come out in jets with equal force from all the openings. This shows that the pressure exerted at one point is transmitted equally in all directions.
Explanation: Consider a vessel full of water and filled with air tight piston in different positions as shown in the diagram.
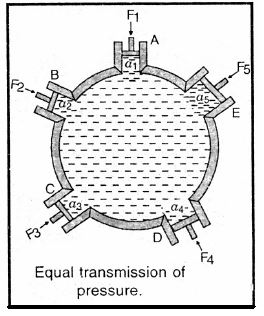
Let the piston at A be pushed down with a force . Pressure P on the piston is
Where ‘’ is the area of cross-section of piston at A. It will be observed that to hold pistons at B, C, D and E we have to apply forces on them such that
where are the areas of cross-section of pistons at B, C, D and E respectively. This indicates that pressure is transmitted equally in all directions as stated by Pascal’s law.
Application of Pascal’s Law
Pascal’s law is used to multiply force in machines such as the hydraulic press or Bramah press, hydraulic lift and
hydraulic brake.
Principle of a Hydraulic Machine
(Hydraulic Press or Bramah Press)
Hydraulic press works on the principle of Pascal’s law.
Construction : It consists of two cylindrical vessels X and Y of different cross sections. Let the cross sectional area of X be ‘A1’ and that Y be ‘A2’
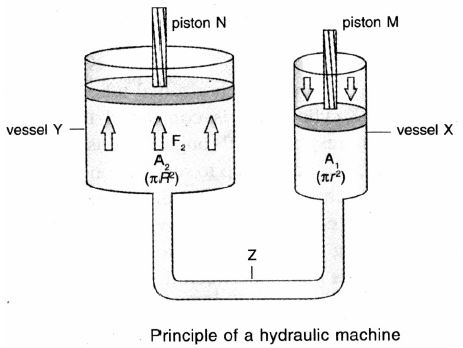
The vessels contain a liquid. The vessel X is provided with water tight piston M. The vessel X has smaller diameter than vessel Y. The vessel Y is provided with watertight piston N. r and R are the radii of vessel X and vessel Y respectively. Let the area of crosssection of vessel X with a smaller diameter be A1 and that of vessel Y be A2. So A2 > A1.
A weight is placed on piston M of the vessel X. It exerts a force F1 on the piston M. Therefore, the pressure applied on piston M in the downward direction is .
According to Pascal’s law, the pressure exerted on the piston M is transmitted by the liquid to the piston N.
The upward pressure exerted on the piston N is .
Hence, the upward force (F2) exerted on piston N is
F2 = Pressure on the piston N × Area [Since force = pressure × area ]
or
Since therefore
Thus a small force F1 applied on the smaller piston M can be used to exert a large force F2 on the bigger piston N. This is the principle of a hydraulic machine
Note: Applying the principle of hydraulic machines, we get :
Mechanical advantage =
Note :
i) Larger piston is generally referred as press plunger
ii) Smaller piston is referred as pump plunger
Uses of Hydraulic Press
1. It is used for compressing the cotton bales and straw.
2. It is used for extracting oil from oil seeds.
3. It is used for punching holes in metals.
4. It is used for giving specific shapes to metal sheets.
5. It is used for servicing automobiles in service stations.
1.21 ATMOSPHERIC PRESSURE
The atmosphere is a mixture of gases. Above the ground, the Earth’s atmosphere extends to a few hundred kilometers in height.
Very close to the Earth’s surface, we find millions of gas molecules in every cubic centimeter.
It is calculated that roughly around molecules per cubic centimeter are present.
These molecules are all zipping around in different directions, colliding into each other and rebounding.
They make an impact on each and every object by bombarding their surface resulting in pressure.
The weight of the atmosphere also exerts force resulting in pressure. This pressure is known as Atmospheric pressure.
The weight of thrust of air exerted on unit area of earth’s surface is called Atmospheric pressure.
It is to be noted that the atmospheric pressure decrease as the altitude increases.
The reason being that the number of molecules present at a higher altitude is less than the number of molecules
present at the sea level.
So, as the number of air molecules decreases with increases in altitude, the air pressure also decrease.
Measurement of Atmospheric Pressure
Atmospheric pressure is measured by using a barometer. It was invented by Torricelli in 1643.
“The Mercury Barometer”
Measurement of Atmospheric Pressure using Barometer
Atmospheric pressure (P) can be obtained by a barometer, using the formula.
P = h × d × g
Where, ‘h’ is the height of liquid column,
‘d’ is the density of the barometeric liquid and ‘g’ is the acceleration due to gravity.
If ‘h’ is expressed in meters, ‘d’ in Kg/m3 and ‘g’ in m/s2, the pressure obtained by this formula is in terms of
‘Newton/m2 or ‘dyne/cm2.
Pressure measured in this way is called Absolute pressure. In the formula ‘P = hdg’, the terms ‘d’ and ‘g’ for a given barometer are constant and the atmospheric pressure is proportional to the height of the mercury column.
1 atm is the pressure exerted by a vertical column of mercury of 76 cm (or 760 mm) height.
1 atm = 76 cm × 13.6 g cm-3 × 9.8 ms–2 (using hdg for pressure exerted by a liquid)
= 0.76 m ×13.6 × 103 kg m-3 × 9.8 ms–2
= 101292.8 N m-2 =1.013×105 Pa
Other units usually used in measurement of pressure are torr and bar
1 torr = 1 mm of Hg, 1 bar = 105 Pa
1.22 BUOYANCE
A four – year child was questioned. ‘How do you wash your hands’ ?
He promptly answered, ‘With the water form the tap’.
A twelve – year boy was questioned: How do you get water in your tap ?
He answered, ‘We have a storage tank the upstairs, which gets filled up when we switch on the motor’.
Okay! This is how, in this modern age, we get water effortlessly. But in most of the villages the situation is entirely
different.
Even agricultural fields are watered by manual drawing, from wells, leave alone the domestic purpose.
For their daily requirements, village people draw water from wells with the help of a bucket tied to a rope.
When the bucket is released into the well, it gets filled up with water and then sinks to a certain depth in water.
Now, try to pull out the rope and observe.
While drawing water form a depth to the surface, we feel that the bucket of water is very light or almost weightless, but when we draw the water from the surface to the required height, we feel some heaviness or weight of water.
From this act, it is clear that an object can be raised or lifted easily inside water.
Heave you ever thought, what makes this raising or lifting easy ?
This is due to the invisible force that is exerted by the liquid on the body in an upward direction.
This upward force is called Buoyant force.
From the above activity, it is very clear that some invisible force acts in upward direction when the body is immersed in water.
This force makes the weight of the body (bucket) less than its actual weight.
The loss in weight is caused due to the upward force acting on the body. It is called buoyant force and the property is called buoyancy.
The upward force which is acting on a body when it is completely or partially immersed in a fluid is called up thrust or the buoyant force, and the phenomenon is known as buoyancy.
Examples of Buoyant Force
1. When we lift a stone in air, we feel it heavier but inside the liquid we feel it to be lighter because water exerts
and invisible force (upthrust) on the body, which decreases the weight of the body.
That is why we feel it lighter inside the water than in the air.
2. When a swimmer jumps into water from a height, he finds himself being pushed towards the surface of the
water without any effort on his part.
3. A stone which is dropped, falls down with an acceleration of 9.8 ms–2 in the air. The same stone (density = 5 g cm-3) moves down in water with an initial acceleration of 7.8 ms–2 due to upward buoyant force.
Cause of Buoyant Force
We know that a liquid contained in a vessel exerts pressure at all points and in all directions.
According to Pascal’s law, the direction of pressure is normal (perpendicular) to the surface of the body.
The pressure at a given point depends on the depth (h) of the point inside the liquid. (P = hdg) Now, consider a body ABCD inside the liquid, as shown in the figure.
i) Side – wise Pressure :
Consider two points ‘x’ and ‘y’ on the sides AD and BC respectively at the same depth as shown in the figure.
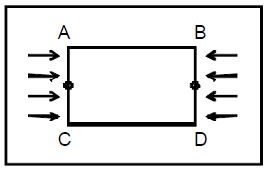
As the depth of these two points is same from the surface, equal thrust acts on them in an opposite direction.
Since the forces are equal in magnitude and acting in the opposite direction they get neutralized.
So, the resultant sidewise pressure is zero on the body. If any resultant force acting on the body is the resultant of the upward and downward pressure.
ii) Upward and Downward Pressure :
The downward pressure acts on the upper surface of the body and an upward pressure acts on its lower surface.
The lower face is at a greater depth than the upper face.
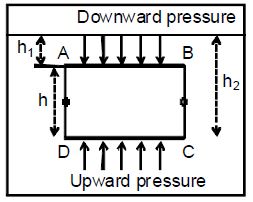
Hence, the upward pressure on the lower face is more than the downward pressure on the upper face.
So, the resultant pressure is in the upward direction.
Therefore, the difference in the upward and downward pressure results in a buoyant force acting upwards.
Result of Buoyant Force
We know that the feeling of easiness to lift an object in water is due to buoyant force.
This is because, the buoyant force neutralizes some downward force acting on the body.
That is, there is a loss in the weight (downward force) of a body due to buoyancy.
1.23 ARCHIMEDES’ PRINCIPLE
Two thousand years ago there lived a Greek philosopher, Archimedes’. He was a scientist in the court of a king. The king had a doubt about the purity of gold with which his crown was made.
So he asked Archimedes to invent a method of testing the purity of gold without spoiling the crown. One day,
Archimedes noticed that when he had entered a fully filled bath tub, some water overflowed. Furthermore, he noticed that he felt considerably lighter in bath the tub. He reasoned that the loss in weight of his body in water must have some connection with the amount of water displaced by his body. He performed a simple experiment and came out with the relation between the apparent loss of weight and the weight of water displaced.
This relation is called Archimedes’ principle.
Let us understand it form the following
Take a spring balance and suspend 200 g stone to it. The weight of the stone in air is found to be 200 gf.
Now, take an empty jar and fill it with water, till the water is one the verge of overflowing.
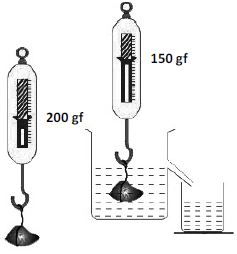
Gently lower the stone, suspended from spring balance, into water, in the jar, till the whole solid is completely immersed. It is observed that the spring balance records less value of weight equal to 150 gf.
This loss of weight is due to buoyant force.
The metal block experiences buoyant force, due to which it loses its weight.
The loss of weight = weight in air – weight in water.
The liquid displaced by the metal block is collected in a beaker and its weight is obtained. Let it be W gf.
It is observed that the weight of the liquid displaced is equal to the loss of weight of the object.
Weight of liquid displaced (W) = loss of weight
We also know,
Loss of weight = Buoyant force ________ (2) (1) = (2)
Hence, we can say that buoyant force is equal to the weight of the liquid displaced.
Thus, we can conclude that
“Whenever a body is partly or wholly immersed in a fluid, it experiences an upward buoyant force which is equal to weight of the liquid displaced by the body”.
This is known as Archimedes’ principle, which, in short, is
Buoyant force = weight of liquid displaced
Calculation of Buoyant Force
We know that buoyant force is equal to the weight of the liquid displaced.
Let the weight of the liquid displaced be ‘mg’.
Buoyant force (mg) = V × d × g
( mass = volume × density)
_____ (1)
If the body is inside the liquid, then the volume of the liquid displaced is equal to the volume of the body, Now the
equation changes as
Buoyant force = _____ (2)
i) Buoyant Force and Volume of Body
Dip an iron block and a thermocol sheet of the same mass into the water.
in which case do you feel the Buoyant force more?
We know, buoyant force =
As they are dipped in the same liquid and at the same place, and g are constants.
Let us check their volumes.
Volume of a body (V)
As mass is same for both the bodies,
As the density of thermocol is less than that of iron, volume of thermocol is more and therefore, it displaces more volume of water.
Therefore, buoyant force is more on the thermocol sheet.
Conclusion: If two bodies of the same mass are immersed in water, then the body with greater volume or less
density experiences more buoyant force.
In other words, the loss of weight is more for the body with greater volume.
ii) Buoyant Force and Density of Liquid
Take two beakers, one filled with water and the other with oil. Try to observe the loss of weight by immersing
the body completely in water and oil separately.
In which case do you feel more loss of weight ?
The loss of weight can be found out, if buoyant force is known.
We know, buoyant force
As the same body is immersed at a given place, and g are constant.
Let us check the densities of water and oil.
As the density of oil is less than the density of water, buoyant force is more for water.
Conclusion: If a body is immersed in water and oil, as the liquid with greater density produces more buoyant force, here, water with greater density produces more buoyant force.
iii) Buoyant Force and Gravity
Take a body of volume ‘V”, and immerse it in a liquid of density dliquid on the surface of the earth and on the
surface of the moon respectively.
In which case do you feel the buoyant force more?
We know, buoyant force =
As the body and liquid are the same on both the surfaces, are constant.
Acceleration due to gravity on the earth is six times greater than the acceleration due to gravity on the moon. So,
buoyant force is more on the earth than on the moon.
Conclusion: A body in a given liquid experiences greater buoyant force at a place with greater value of ‘g’.
Planets on which a body experiences highest and least Buoyant Force
Of all the planets, the value of ‘g’ is least for Pluto and the planet with greater value of ‘g’ is Jupiter.
So, buoyant force for a body in a liquid is the least on Pluto and greater on jupiter.
The value of ‘g’ on Saturn is almost equal to that on earth.
Hence, buoyant force experienced by a body in a given liquid on Saturn is the same as that on the earth.
1.24 FLOATATION
Consider the following cases:
Case-1: Stone in water
A stone in water is acted upon by two forces as shown.

In the case of a stone, the downward weight is greater than the upward buoyant force and
hence, the stone sinks down.
Case- 2: Air balloon in water
An air balloon in water is acted upon by two forces as shown.
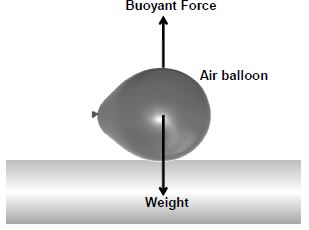
In the case of a hydrogen balloon, the upward buoyant force is more than the downward weight and hence, the balloon moves up.
Case-3: Wood in Water
What happens if the weight of the body is equal to the buoyant force ?
If the weight of the body is equal to the buoyant force, the body neither sinks like the stone nor moves up like the balloon. But it floats.
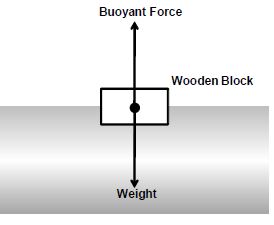
So, floating is an equilibrium state, where the buoyant force acting upwards on a body is equal to its weight acting downwards.
Conditions
1. Sinking of a Body
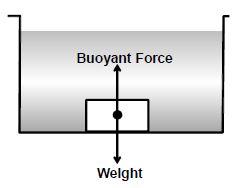
A body sinks if Weight of body > Buoyant force
A body sinks if its density is more than that of the liquid.
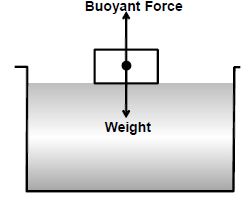
2. Flotation of a Body
A body floats if Weight of body = Buoyant force.
A body floats if its density body is equal to that of the liquid.
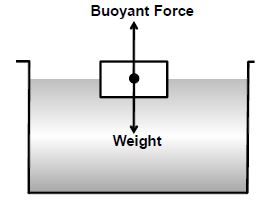
3. Upward Motion of a Body
A body will move up in a fluid if Weight of body < Buoyant force.
.
A body floats over the surface in a fluid if density of the body is less than that of the liquid.
1.25 RELATIVE DENSITY
Density
Density of a substance is defined as its mass per unit volume,
i.e.,
The SI unit of density is kg m-3. Its CGS unit is gcm-3.
Let us consider mercury of density 13.6 g cm-3, alcohol of density 0.8 g cm-3 and aluminium of density 2.7 g cm-3.
If you compare the densities of mercury and aluminium, aluminium has less density than mercury, whereas if you
compare aluminium and alcohol, aluminium is denser than alcohol.
In this way, any substance can be heavier or lighter when compared to the other substance.
To avoid this confusion, another term is devised, which is called relative density.
In relative density, the density of a substance is compared to the density of water at 4 °C.
The relative density of a substance is the ratio of the density of the
substance to the density of water at 4°C.
Relative density of a substance
_____ (1)
Note:
i) Relative density is also known as specific gravity.
ii) Relative density is the ratio of densities. So, it has no unit, but is a pure number.
Significance of Relative Density
Relative density of a substance tells us how many times a substance is denser than water.
Example: If the relative density of a substance is ‘6’, it means that the substance is 6 times denser than water.
Relative Density in terms of Weight of Body and Weight of Water displaced by the Body
We know, Relative density =
Relative Density =
If the volume of a substance is equal to the volume of the water, then,
Relative density
Multiplying the numerator and the denominator by ‘g’, then, we get,
Relative density
_____ (2)
We know that the weight of equal volume of water is equal to the loss of weight of the body in water.
Loss of weight in water = Weight in air – Weight in water = Weight of water displaced _________ (3)
Using (2) and (3), we can write
Relative density of a body _________ (4)
Relative density of a body = _________ (5)
Determination of Specific Gravity or Relative Density of Liquids
Take a body which sinks in both the liquid and the water. Determine its weight in air, let it be .
Now, determine its weight in the given water and liquid with a spring balance. Let it be and respectively.
The body displaces the liquid equal to its volume(V)
Loss of weight of the body in water = Weight of the body in air – Weight of the body in water
=
Loss of weight of the body in the given liquid = weight of the body in air – weight of the body in liquid =
Relative density of liquid =
But, we know that the weight of V volume of liquid = loss of weight of the body in liquid.
Similarly, weight of ‘V’ volume of water = loss of weight of the body in water.
Relative density =
Relative density =
By substituting the measured values of , the relative density of the liquid can be determined.








