16.1. INTRODUCTION
Dealing with numbers has been quite interesting. There are many tricks and puzzles of numbers that we may like to solve. In this Chapter, by using algebra, we shall learn how such tricks and puzzles can be scientifically worked out.
16.2. NUMBERS IN GENERALISED FORM
We have learned to write a number in the expanded form. For example, we can write.
76 as 70 + 6 = 10 × tens digit + one digit
213 as 200 + 10 + 3 = 100 × hundreds digit + 10 × tens digit + ones digit
2498 as 2000 + 400 + 90 + 8 = 1000 × thousands digit + 100 × hundreds digit + 10 × tens digit + ones digit Thus,
A 2-digit number whose tens digits is ‘a’ and ones digit is ‘b’ can be written as 10a + b, where a( 0) and b are whole numbers from 0 to 9.
Similarly, we can write a 3-digit or a 4-digit number as follows
1. A 3-digit number with hundreds digit ‘a’; tens digit ‘b’ and ones digit ‘c’ is written as 100a + 10b + c, where a0 (in short, as abc)
2. A 4-digit number with thousands digit ‘a’; hundreds digit ‘b’, tens digit ‘c’ and ones digit ‘d’ is written as 1000a + 100b + 10c + d (in short, as abcd).
Example 1 : What is the general form of the following numbers ?
(a) 375
(b) 901
(c) ps
(d) 5z7
Solution : (a) General form of 375 = 300 + 70 + 5 = 100 × 3 + 10 × 7 + 5
(b) General form of 901 = 900 + 0 + 1 = 100 × 9 + 10 × 0 + 1
(c) General form of ps = 10 × p + s = 10p + s
(d) General form of 5z7 = 500 + 10z + 7 = 100 × 5 + 10 × z + 7
Example 2 : Write the following expressions in their usual form.
1. 100 × x + 10 × z+ r
2. 100 × 7 + 10 × 2 + 0
Solution : (a) Usual form of 100 × x + 10 × z + r = 100x + 10z + r = xzr
(b) Usual form of 100 × 7 + 10 × 2 + 0 = 700 + 20 + 0 = 720
16.3. GAMES WITH NUMBERS
Let us enjoy some games with numbers.
1. Reversing the digits – 2-digit number
Property 1 :
| The sum of a two-digit number and the number obtained by reversing its digits is always divisible 11. |
Think of any 2-digit number, say : 47
Reverse its two digits and get a new number : 74
Add the two numbers : 47 + 74, i.e., 121
Divide the sum by 11 : 121 11, i.e., 11
How does it work ?
Let the 2-digit number be ab.
Then, ab + ba = (10a + b) + (10b + a)
= 11a + 11b = 11(a + b)
(ab + ba) 11 = 11(a + b) 11 = a + b.
Property 2 :
| The difference between a two-digit number and the number obtained by reversing its digits is always divisible by 9. |
Think of any 2-digit number say : 38
Reverse its two digits and get a new number : 83
Subtract the smaller number from the greater : 83 – 38, i.e., 45
Divide the difference by 9 : 45 9, i.e., 5
How does it work ?
Let the 2-digit number be ab.
Then, ab – ba = (10a + b) – (10b + a)
= 9a – 9b = 9(a – b)
(ab – ba) 9 = 9(a – b) 9 = a – b.
Property 3 :
Reversing the digits – 3-digit number
| The difference between a three digit number and the number obtained by reversing its digits is always divisible by 99. |
Think of a 3-digit number, say : 249
Reverse its three digits and get a new number : 942
Subtract the smaller number from the greater number : 942 – 249, i.e., 693
Divide the difference by 99. 693 99 i.e., 7
How does it work ?
Let the 3-digit number be abc.
Then, abc – cba = (100a + 10b + c) (100c + 10b + a)
= 99a – 99c
= 99 (a – c)
So, (abc – cba) 99 = 99 (a – c) 99 = a – c
Property 4
If a three digit number has the same digit in its hundreds and one’s places, then the difference between the number and the number formed by reversing its digit is always zero.
abc = 100a + 10b + c
cba = 100c + 10b + a
abc – cba = 0, when a = c, a – c = 0
Forming 3-digit number, with given three digits.
Property 5 :
The sum of three or more three-digit numbers obtained by re-arranging the digits of a three digit number is always divisible by 37 & 3, whatever be the values of a, b, c.
Let three digit numbers abc.
Then, abc = 100a + 10b + c
cab = 100c + 10a + b
bca = 100b + 10c + a
Sum of these three number we can get 111a + 111b + 111c = 3 × 37 (a + b + c)
16.4. LETTERS FOR DIGITS
We all are familiar with puzzles in books, magazines, newspapers etc. Here, we introduce a new type of puzzle where you will need to find some missing numbers using the basic properties of mathematics. Let us look at the following puzzle.
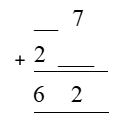
How can we find the missing numbers ?
In the first column, the sum of 7 and another digit cannot be 2, as 2 is less than 7. Hence, it is logical that the number may be 12 as 7 + 5 = 12.
Thus, in the first column the missing number is 5.
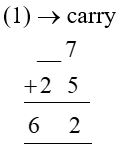
The second column has a carryover value of 1.
Thus, it becomes 1 + 2 + ___ = 6
Now, it is clear that the missing number is 3.
Therefore, we can write
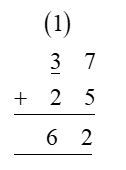
We can also write the same problem as
Here, the digits are denoted by the letters of the English alphabet and only one digit is denoted by one letter.
For example, let us try to find the value of A in the following example.
Here, we add a digit three times and get the same digit at the units place.
Such digits are 0 and 5.
If we take A as 0, then the addition of three 0s equals 0. However, we cannot get any number in the tens place. In the problem, we can see that the sum has 1 in its tens place. Let us now take the digit 5 as the value of A.
If A = 5, then
Therefore, the value of A is 5.
Example 3 : Find the values of the letters in the following puzzles :
(i)
(ii)
(iii)
Solution :
(i) We have
Here, the sum of A and 2 is 6.
Thus, A can be 4.
On replacing letter A with its value i.e., 4, the puzzle becomes
We can see that the sum of B and B is 6.
Thus, B can be 3
Hence, the value of A is 4 and the value of B is 3.
(ii) We have
Here, the ones digit of A × 3 = A.
Thus, A must be 0 or 5.
If we take A = 0, then the puzzle becomes
But 30 × 3 = 90 ≠ 100
Therefore, we take A = 5.
This gives us the correct product, as given in the puzzle.
Hence, the answer is A = 5.
(iii) We have
In the puzzle, we have 6 × Q = Q at the units place.
Hence, Q may be 0, 2, 4, 6, or 8.
If we take Q = 0, then the puzzle becomes
This can only be possible if P = 0.
Since P and Q are different numbers, this answer is not acceptable.
Let us now take Q = 2.
On doing so, the puzzle becomes
We know that 37 × 6 = 222. However, this is not our answer because 2 is not at the units place in the number 37.
Let us now take Q = 4.
On doing so, the puzzle becomes
We know that 74 × 6 = 444. Hence, the value of P is 7.
If we take Q = 6, then the puzzle becomes
However, 111 × 6 = 666
This cannot be our answer because 6 is not at the units place of 111 and 111 is a three-digit number.
If we take Q = 8, then the puzzle becomes
However, 148 × 6 = 888
This cannot be our answer because 148 is a three-digit number. Replace A, B, C by suitable numerals.
16.5. TESTS OF DIVISIBILITY
Hotel Grand Mansion has 432 rooms and 10 floors. Surbhi, who went to the hotel for the first time with her sister Shweta, was quite amazed by the numbers. She asked Shweta if she could tell whether each of the floors had the same number of rooms. Shweta replied that this is not possible as 432 is not exactly divisible by 10.
Surbhi wanted to check if what Shweta said was true. She quickly divided the numbers as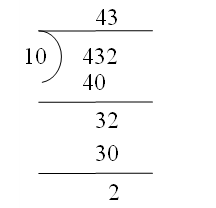
She found that since the remainder is 2, 432 is not exactly divisible by 10.
Shweta had also said that the number 432 is not divisible by 10.
There is a rule to check if a number is divisible by 10.
We can save the time used in division by applying this rule.
The rule to check whether a number is divisible by 10 or not is as follows :
| A number is said to be divisible by 10 if the digit at the units place is 0. |
For example,25690 is divisible by 10 as the digit at its units place is 0, whereas 759 is not divisible by 10 as the digit at its units place is 9.
Using this method, one can check the divisibility of a number by 10 without doing the actual division.
Divisibility of a Number by 5
In a school, there were 495 students in Grade 8. The students had to be divided among the 5 houses of the school. The school’s principal asked the students whether they will be divided equally among the five houses or will there be some houses with more students than the other houses. Dinesh, the topper of Grade 8, instantly said that the 495 students could be equally divided into 5 houses. While Ashish, Dinesh’s rival, did the following. 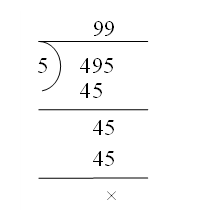
Ashish said that when 495 is divided by 5, the remainder is 0. Hence, 495 is divisible by 5.
We can see that although both Ashish and Dinesh gave the same answer, Ashish took more time to give the answer.
Dinesh used the divisibility rule of 5. This rule saved him the time that he would have otherwise used in actual division.
The rule to check whether a number is divisible or not is as follows :
| A number is said to be divisible by 5 if the digit at its units place is 0 or 5. |
For example, numbers such as 14365, 256030, 1720, 985, 3685 etc. are divisible by 5 as the digits at the units places of these numbers are either 0 or 5. However, numbers such as 7586, 6523, 458 etc. are not divisible by 5 as the digits at the units places of these numbers are neither 5 nor 0.
We use this method to check the divisibility of a number by 5 without performing the actual division.
Divisibility of a Number by 2
Ashok was standing with his friend Nikhil at a bus stop. The first bus that came was of route 432. Ashok looked at it and said to Nikhil that the route number of the bus was divisible by 2. Nikhil wanted to verify what Ashok had said and started calculating in his notebook. This is what he did
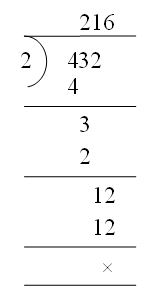
Although he verified what his friend had said, Nikhil was amazed at Ashok’s quick calculation. He asked Ashok how he did it.
Ashok said he used a trick to check the divisibility of 432 by 2.
Ashok used the following rule :
| A number is said to be divisible by 2 if the digit at its units place is 2, 4, 6, 8, or 0. |
For example, numbers such as 4782, 69120, 5736, 9218, 724 etc. are divisible by 2 as the digits at the units places of the numbers are 2, 4, 6, 8, or 0, whereas numbers such as 817, 1221, 5693, 625, 8569 etc. are not divisible by 2 as the digits at the units places of these numbers are not 2, 4, 6, 8, or 0.
We use this method to check the divisibility of a number by 2 without performing the actual division.
Divisibility of a Number by 3 and 9
Imagine if you had to check if numbers such as 27, 18, or 33 were divisible by 3 and 9. You will obviously check it mentally and give the answer without performing any long division. But what if you are asked to check if the number 123456789 is divisible by 3 and 9? You will take a lot of time calculating the divisibility of the number with both 3 and 9 before you give the answer.
A teacher asked the students in a class to check whether 624 is divisible by 3 and 9. Mayank said that 624 is divisible by 3 but not divisible by 9 by just looking at the number. Shikhar, another student, started performing the divisions.
This is what Shikhar did.
Although Shikhar and Mayank gave the same answer, Mayank took very little time to give the answer, while Shikhar had to perform the division.
Mayank used two rules of divisibility to get the answer. These can be stated as follows :
| A number is said to be divisible by 3 if the sum of its digits is divisible by 3. |
| A number is said to be divisible by 9 if the sum of its digits is divisible by 9. |
For example, we can say that444 is divisible by 3 without performing the division.
Here is what we can do.
Sum of digits = 4 + 4 + 4= 12
12 is divisible by 3.
Hence, 444 is divisible by 3.
Similarly, we can say that 234 is divisible by 9 without performing the division.
Here is what we can do.
2 + 3 + 4 = 9
9 is divisible by 9. Hence, 234 is divisible by 9.
Let us once again look at the number Mayank and Shikhar were working on.
Sum of the digits of the number 624 = 6 + 2 + 4 = 12
12 is divisible by 3 but not by 9. Hence, 624 is divisible by 3 but not by 9.








