Factorizations

14.1 INTRODUCTION
In earlier classes, we have learnt about prime factorization of natural number.
For example, 600 = 2³ × 3 × 5²
In algebra too, we can express an algebraic expression as a product of simpler expressions. For example,
5x (x + 3) = 5 × x × (x + 3)
Here, the factor 5, x and (x + 3) are irreducible factors of 5x (x + 3).
The process of expressing an algebraic expression as a product of its irreducible factors is called factorization.
In this chapter, we study about the process of factorization of several kinds of algebraic expressions. Depending on the given expression, there are many ways to do factorization. Let us study them one by one.
14.2. FACTORIZATION OF ALGEBRAIC EXPRESSIONS
You know about the prime factorization of numbers. Let us revise the method of prime factorization by taking the example of the number 210.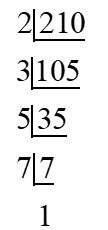

We can write 210 as a product of 2, 3, 5, and 7.
Hence, 210 = 2 × 3 × 5 × 7
Here, 2, 3, 5, and 7 are the prime factors of 210. In the same way, we can factorize any expression, i.e., we can write any expression as a product of its factors.
For example, 2xyz = 2 × x × y × z
Here, 2, x, y, and z are the factors of 2xyz, and we cannot further reduce them.
Thus, we say that 2, x, y, and z are the irreducible factors of 2xyz.
(a) Method of common factors
Let us try to find the factors of 2x + 4.
We shall write each term as a product of irreducible factors;
2x = 2 × x
4 = 2 × 2
Hence 2x + 4 = (2 × x) + (2 × 2)
Notice that factor 2 is common to both the terms.
Observe, by distributive law
2 × (x + 2) = (2 × x) + (2 × 2)
Therefore, we can write
2x + 4 = 2 × (x + 2) = 2 (x + 2)
Thus, the expression 2x + 4 is the same as 2 (x + 2). Now we can read off its factors they are 2 and (x + 2). These factors are irreducible.
Next, factorise 5xy + 10x.
The irreducible factor forms of 5xy and 10x are respectively,
5xy = 5 × x × y
10x = 2 × 5 × x
Observe that the two terms have 5 and x as common factors. Now,
5xy + 10x = (5 × x × y) + (5 × x × 2) = (5x × y) + (5x × 2)
We combine the two terms using the distributive law,
(5x × y) + (5x × 2) = 5x × (y + 2)
Therefore, 5xy + 10x = 5 x (y + 2). (This is the desired factor form.)
Let us discuss some more examples.
Example 1 : Find the common factors of the terms 6pq, 8p², and 4pq².
Solution : Write the factors of each term.
6pq = 2 × 3 × p × q
8p² = 2 × 2 × 2 × p × p
4pq² = 2 × 2 × p × q × q
Here, 2 and p are the common factors of the given terms 6pq, 8p², and 4pq²
Example 2 : Factorize the following expressions :
(i) 7x² + 14x
(ii) 4a²bcx²y³z⁴ − 5ab²cx³y⁴z² + 7abc²x⁴y²z³
(iii) −4a² + 3p³ − 5b
Solution : (i) Write the factors of each term.
7x² = 7 × x × x
14x = 2 × 7 × x
Here, 7 and x are the common factors.
7x² + 14x = 7 × x × x + 2 × 7 × x
= 7 × x (x + 2) = 7x (x + 2)
(ii) Write the factors of each term.
4a² bcx² y³z⁴ = 2 × 2 × a × a × b × c × x × x × y × y × y × z × z × z × z
− 5ab² cx³ y⁴ z² = − 5 × a × b × b × c × x × x × x × y × y × y × y × z × z
7abc² x⁴ y² z³ = 7 × a × b × c × c × x × x × x × x × y × y × z × z × z
Here, a, b, c, x, x, y, y, z, and z are the common factors of given terms.
Hence, 4a² bcx² y³ z⁴ – 5ab² cx³ y⁴ z² + 7abc² x⁴ y² z³

^{$=a\times b\times c\times x^2\times y^2\times z^2\left\{\begin{array}{l}2\times 2\times a\times y\times z\times z–5\times b\times x\times y\times y\\ +7\times c\times x\times x\times z\end{array}\right\}$}
= abcx² y² z² (4ayz² – 5bxy² + 7cx² z)
(iii) Write the factors of each term.
−4a² = −2 × 2 × a × a
3p³ = 3 × p × p × p
−5b = −5 × b
There is no common factor of these terms other than 1.
(b) Factorisation by regrouping terms
Look at the expression 2xy + 2y + 3x + 3. You will notice that the first two terms have common factors 2 and y and the last two terms have a common factor 3. But there is no single factor common to all the terms. How shall we proceed ?
Let us write (2xy + 2y) in the factor form :
2xy + 2y = (2 × x × y) + (2 × y)
= (2 × y × x) + (2 × y × 1)
= (2y × x) + (2y × 1) = 2y (x + 1)
Similarly, 3x + 3 = (3 × x) + (3 × 1)
= 3 × (x + 1) = 3 (x + 1)
Hence, 2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x +1)
Observe, now we have a common factor (x + 1) in both the terms on the right hand side.  
Combining the two terms,
2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x + 1) = (x + 1) (2y + 3)
The expression 2xy + 2y + 3x + 3 is now in the form of a product of factors. Its factors are (x + 1) and (2y + 3). Note, these factors are irreducible.
Example 3 : Factorize the following expressions :
(i) 2x + ax − 2y – ay
(ii) 2a + 3b − 2 − 3ab
Solution : (i) The given expression is 2x + ax − 2y − ay.
We can factorize this expression as
2x + ax − 2y − ay = (2x − 2y) + (ax − ay)
=2 (x − y) + a (x − y)
= (x − y) (2 + a)
= (x − y) (2 + a)
(ii) The given expression is 2a + 3b − 2 − 3ab.
We can factorize this expression as
2a + 3b − 2 − 3ab = (2a − 2) + (−3ab + 3b)
= 2 (a − 1) + (−3b) (a − 1)
= 2 (a − 1) − 3b (a − 1)
= (a − 1) (2 − 3b)
14.3. FACTORISATION USING IDENTITIES
(a) Factorisation of Algebraic Expressions Using Identities (a + b)², (a − b)², and a² − b²
We know the identities
(i) a² + 2ab + b² = (a + b)²
(ii) a² − 2ab + b² = (a − b)²
(iii) a² − b² = (a + b) (a − b)
We can use these identities to factorise algebraic expressions as well. Let us discuss each identity one by one.
(i) Application of the identity a² + 2ab + b² = (a + b)² to factorise an algebraic expression
Let us factorise the expression x² + 6x + 9.
This expression, the first term is the square of x, the last term is the square of 3, and the middle term is positive and is twice the product of x and 3.
Thus, x² + 6x + 9 can be written as
x² + 6x + 9 = (x)² + 2 × x × 3 + (3)²
The right hand side of this expression is in the form of a² + 2ab + b², where a = x and b = 3.
We know the identity a² + 2ab + b² = (a + b)².
$\therefore$ (x)² + 2 × x × 3 + (3)² = (x + 3)²
Thus, x² + 6x + 9 = (x + 3)².
(ii) Application of the identity a² − 2ab + b² = (a − b)² to factorise an algebraic expression
Let us factorise the expression 9y² − 12y + 4.
In this expression, the first term is the square of 3y, the last term is the square of 2, and the middle term is negative and is twice of the product of 3y and 2.
Thus, 9y² − 12y + 4 can be written as
9y² − 12y + 4 = (3y)² − 2 × 3y × 2 + (2)²
The right hand side of this expression is in the form of a² − 2ab + b², where a = 3y and b = 2.
We know the identity a² − 2ab + b² = (a − b)².
$\therefore$ (3y)² − 2 × 3y × 2 + (2)² = (3y − 2)²
Thus, 9y² − 12y + 4 = (3y − 2)².
(iii) Application of the identity a² − b² = (a + b) (a − b) to factorise an algebraic expression
We use this identity when an expression is given as the difference of two squares.
Let us factorise the expression x² − 25.
We can write it as x² − 25 = (x)² − (5)²
The right hand side of this expression is in the form of a² − b², where a = x and b = 5
On using the identity a² − b² = (a + b) (a − b), we obtain
x² − 25 = (x + 5) (x − 5)
Thus, (x + 5) and (x − 5) are the factors of x² − 25.
To factorize an algebraic expression, we have to observe the given expression. If it has a form that fits the left-hand side of one of the identities mentioned in the beginning, then the expression corresponding to the right-hand side of the identity gives the desired factorization.
Let us discuss some more examples based on what we have discussed so far.
Example 4 : Factorise the given expressions.
1. 25x²+ 40xy + 16y²
2. 81x³ + x − 18x²
3. (p + 1)² − (p − 1)²
4. 16a²− 25b² + 60bc − 36c²
5. al² − bm² − am² + bl²
6. 81x⁴ − 256 y⁴
7. 16x⁴− (3a + 5c)⁴
Solution :
(1) The given expression is 25x² + 40xy + 16y².
25x² + 40xy + 16y² = (5x)² + 2 × 5x × 4y + (4y)²
= (5x + 4y)² [a² + 2ab + b² = (a + b)²]
$\therefore$ 25x² + 40xy + 16y² = (5x + 4y)²
(2) The given expression is 81x³ + x − 18x².
Here, x is a factor common to all terms in the expression.
$\therefore$ 81x³ + x − 18x² = x (81x² + 1 − 18x)
= x [(9x)² + (1)² − 2 × 9x × 1]
= x [9x − 1]² [a² − 2ab + b² = (a − b)²)
$\therefore$ 81x³ + x − 18x² = x (9x − 1)²
(3) The given expression is (p + 1)² − (p − 1)².
On using the identity a² − b² = (a + b) (a − b), we obtain
(p + 1)² − (p − 1)² = {(p + 1) + (p − 1)} {(p + 1) − (p − 1)}
= (p + 1 + p − 1) (p + 1 − p + 1) = (2p) (2) = 4p
$\therefore$ (p + 1)² − (p − 1)² = 4p
(4) The given expression is 16a² − 25b² + 60bc − 36c².
16a² − 25b² + 60bc − 36c²
= 16a² − (25b² − 60bc + 36c²)
= (4a)² − {(5b)² − 2 (5b) (6c) + (6c)²}
= (4a)² − (5b − 6c)² [Using the identity a² − 2ab + b² = (a − b)²]
= {(4a) + (5b − 6c)}{(4a) − (5b − 6c)}[Using the identity a² − b² = (a + b) (a − b)]
 = (4a + 5b − 6c) (4a − 5b + 6c)
(5) The given expression is al² − bm² − am² + bl².
al² − bm² − am² + bl²
= al² − am² + bl² − bm² {Regrouping the terms}
= a (l² − m²) + b (l² − m²)
= (l² − m²) (a + b)
= (l + m) (l − m) (a + b) [Using the identity a² − b² = (a + b) (a − b)]
(6) The given expression is 81x⁴ − 256y⁴.
81x⁴ − 256y⁴   
= (9x²)² – (16y²)²
= (9x² + 16y²) (9x² – 16y²) [Using the identity a² – b² = (a + b) (a – b)]
= (9x² + 16y²) {(3x)² – (4y)²}
= (9x² + 16y²) (3x + 4y) (3x – 4y) [Using the identity a² – b² = (a + b) (a – b)]         
(7) The given expression is 16x⁴ − (3a + 5c)⁴.
16x⁴ − (3a + 5c)⁴
= (4x²)² – [(3a + 5c)²]²
= {4x² + (3a + 5c)²}{4x² – (3a + 5c)²} [a² – b² = (a + b) (a – b)]
= (4x² + 9a² + 30ac + 25c²){(2x)² – (3a + 5c)²}
= (4x² + 9a² + 30ac + 25c²) {(2x) + (3a + 5c)} {(2x) – (3a + 5c)}
[a² – b² = (a + b) (a – b)]
= (4x² + 9a² + 30ac + 25c²) (2x + 3a + 5c) (2x – 3a – 5c)
(b) Factorisation of Algebraic Expressions Using the Identity (x+a) (x+b) = x² + (a + b)x + ab
How can we factorise the algebraic expression x² + 8x + 15 ?
Note that we cannot express this expression as (a + b)² since 15 is not the square of any natural number. What do we do in such a case ?
In this case, we can use the identity x² + (a + b) x + ab = (x + a) (x + b).
If we compare x² + 8x + 15 with x² + (a + b) x + ab, then we obtain a + b = 8 and ab = 15.
Hence, we need to find two numbers, a and b, such that their sum is 8 and their product is 15.
The only numbers that fulfill these two conditions are 3 and 5.
Hence, we can write x² + 8x + 15 as
 x² + 8x + 15 = x² + (5 + 3) x + 5 × 3
= x² + 5x + 3x + 5 × 3
= (x² + 5x) + (3 × x + 5 × 3) = x(x + 5) + 3(x + 5)
= (x + 5) (x + 3) {Taking a common factor from each group}
Let us practice some more questions based on this concept.
Example 5 : Factorise the expression x² − x − 42.
Solution : On comparing x² − x − 42 with x² + (a + b) x + ab, we obtain a + b = −1 and ab = −42.
Here, we have to find two numbers, a and b, such that their sum is −1 and their product is −42.
Since the product (−42) of the numbers a and b is negative and their sum (−1) is also negative, we have to choose two numbers such that the bigger number is negative and the smaller number is positive.
The numbers that fulfill these conditions are −7 and 6.
Thus, obtain a + b = −1 and ab = −42.
Hence, x² − x − 42 = x² − 7x + 6x − 42 = x (x − 7) + 6 (x − 7) = (x − 7) (x + 6)
Example 6 : Factorise the expression y² − 13y + 36.
Solution : On comparing the expression y² − 13y + 36 with y² + (a + b) y + ab, we obtain
a + b = −13 and ab = 36.
Since the product (36) of the numbers a and b is positive and their sum (−13) is negative,  
we have to choose two negative numbers.
The numbers that fulfill these conditions are −9 and −4.
$\therefore$ y² − 13y + 36 = y² − 4y − 9y + 36 = y (y − 4) − 9 (y − 4) = (y − 4) (y − 9)
14.4. DIVISION OF ALGEBRAIC EXPRESSIONS
(a) Division of a monomial by another monomial
Division is exactly the opposite of multiplication. For example, if 4 × 5 = 20, then it is also correct to say that 20 ÷ 5 = 4 and 20 ÷ 4 = 5.
We can use the same concept to divide algebraic expressions.
Let us try to divide the expression 3x by 3 and x.
We can factorize 3x as 3 × x.
This means that 3x is a product of 3 and x.
$\therefore$ 3x ÷ 3 = x and 3x ÷ x = 3
Each of the expressions i.e., 3, x, and 3x is a monomial. Hence, these were examples of division of monomials by monomials.
When we divide a monomial by another monomial, we first need to factorise each monomial.      
Next, we divide the monomial by cancelling the common factors.
(b) Division of a polynomial by a monomial   
Let us consider the division of the trinomial 4y³ + 5y² + 6y by the monomial 2y.
 4y³ + 5y² + 6y = (2 × 2 × y × y × y) + (5 × y × y) + (2 × 3 × y)
(Here, we expressed each term of the polynomial in factor form) we find that 2 × y is common in each term. Therefore, separating 2 × y from each term.
We get 4y³ + 5y² + 6y = 2 × y × (2 × y × y) + 2 × y ×$\left(\frac{5}{2}\times y\right)$+2 × y × 3
$=2y\left(2y^2\right)+2y\left(\frac{5}{2}y\right)+2y\left(3\right)$
$=2y\left(2y^2+\frac{5}{2}y+3\right)$ (The common factor 2y is shown separately.
Therefore, (4y³ + 5y² + 6y) $÷$ 2y
$=\frac{4{\mathrm{y}}^3+5{\mathrm{y}}^2+6\mathrm{y}}{2\mathrm{y}}=\frac{2\mathrm{y}\left(2{\mathrm{y}}^2+\frac{5}{2}\mathrm{y}+3\right)}{2\mathrm{y}}=2{\mathrm{y}}^2+\frac{5}{2}\mathrm{y}+3$
Alternatively, we could divide each term of the trinomial by themonomial using the cancellation method.
$\left(4y^3+5y^2+6y\right)÷2y=\frac{4y^3+5y^2+6y}{2y}$
$=\frac{4y^3}{2y}+\frac{5y^2}{2y}+\frac{6y}{2y}=2y^2+\frac{5}{2}y+3$
Let us discuss some more examples.
Example 7 : Divide the following expressions :
(i). 27x²y²z ÷ 27xyz
(ii). 144pq²r ÷ (−48qr)
Solution : (i) 27x²y²z ÷ 27xyz
Dividend = 27x²y²z
= 3 × 3 × 3 × x × x × y × y × z
Divisor = 27xyz
= 3 × 3 × 3 × x × y × z
$\Rightarrow \frac{27{\mathrm{x}}^2{\mathrm{y}}^2{\mathrm{z}}^2}{27\mathrm{xyz}}=\frac{3\times 3\times 3\times \mathrm{x}\times \mathrm{x}\times \mathrm{y}\times \mathrm{y}\times \mathrm{z}}{3\times 3\times 3\times \mathrm{x}\times \mathrm{y}\times \mathrm{z}}=xy$
$\therefore$ 27x²y²z ÷ 27xyz = xy
(ii) 144pq²r ÷ (−48qr)
Dividend = 144 pq²r
= 2 × 2 × 2 × 2 × 3 × 3 × p × q × q × r
Divisor = −48 qr
= −2 × 2 × 2 × 2 × 3 × q × r
$\Rightarrow \frac{144{\mathrm{pq}}^2\mathrm{r}}{–48\mathrm{qr}}=\frac{2\times 2\times 2\times 2\times 3\times 3\times \mathrm{p}\times \mathrm{q}\times \mathrm{q}\times \mathrm{r}}{–2\times 2\times 2\times 2\times 3\times \mathrm{q}\times \mathrm{r}}$
= −3 × p × q
= −3 pq
$\therefore$ 144pq²r ÷ (− 48qr) = −3pq
Example 8 : Carry out the following divisions :
(i) (x³y⁶ − x⁶y³) ÷ x³y³ 
(ii) 26xy (x + 5) ÷ 13xy
(iii) 27 (−a²bc + ab²c − abc²) ÷ (−3abc)
Solution :
(i) (x³y⁶ − x⁶y³) ÷ x³y³
Dividend = x³y⁶ − x⁶y³= x³y³ (y³ − x³)
Divisor = x³y³

$\Rightarrow \frac{x^3{y}^6–x^6{y}^3}{x^3{y}^3}=\frac{x^3{y}^3\left(y^3–x^3\right)}{x^3{y}^3}=y^3–x^3$
Another method of simplifying this expression is

^{$\frac{x^3{y}^6–x^6{y}^3}{x^3{y}^3}=\frac{x^3{y}^6}{x^3{y}^3}–\frac{x^6{y}^3}{x^3{y}^3}=y^3–x^3$}
$\therefore$ (x³y⁶ − x⁶y³) ÷ x³y³ = y³ − x³
(ii) Dividend = 26xy (x + 5)
= 2 × 13 × x × y × (x + 5)
Divisor = 13xy
= 13 × x × y
$\therefore \frac{26\mathrm{xy}(\mathrm{x}+5)}{13\mathrm{xy}}=\frac{2\times 13\times \mathrm{x}\times \mathrm{y}\times (\mathrm{x}+5)}{13\times \mathrm{x}\times \mathrm{y}}$
= 2 (x + 5)
= 2x + 10
$\therefore$ 26xy (x + 5) ÷ 13xy = 2x + 10
(iii). 27 (−a²bc + ab²c − abc²) $÷$ (−3abc)

$=\frac{27\left(–a^{2}bc+a{b}^{2}c–ab{c}^2\right)}{(–3abc)}$

$=\frac{–27{\mathrm{a}}^2\mathrm{bc}+27{\mathrm{ab}}^2\mathrm{c}–27{\mathrm{abc}}^2}{–3\mathrm{abc}}$

$=\left(\frac{–27a^{2}bc}{–3abc}\right)+\left(\frac{27a{b}^{2}c}{–3abc}\right)+\left(\frac{–27ab{c}^2}{–3abc}\right)$

= 9a – 9b + 9c
(c) Division of Polynomials by Polynomials
 Consider (7x² + 14x) $÷$ (x + 2)
We shall factorise (7x² + 14x) first to check and match factors with the denominator :
7x² + 14x = (7 × x × x) + (2 × 7 × x)
= 7 × x × (x + 2) = 7x(x + 2)
Now (7x² + 14x) $÷$ (x + 2) = $\frac{7x^2+14x}{x+2}$
= $\frac{7x(x+2)}{x+2}$ = 7x  (Cancelling the factor (x + 2))
Let us discuss some more examples.
Example 9 : Factorise the following expressions and divide as directed.
(i). 6ab (9a² − 16b²) ÷ 2ab (3a + 4b)
(ii). (x² − 14x − 32) ÷ (x + 2)
(iii). 36abc (5a − 25) (2b − 14) ÷ 24(a − 5) (b − 7)
Solution : (i) We can factorise the given expressions as
6ab (9a² − 16b²) = 2 × 3 × a × b [(3a)² − (4b)²]
= 2 × 3 × a × b [(3a + 4b) (3a − 4b)] [a² − b² = (a + b)(a − b)]
And, 2ab (3a + 4b) = 2 × a × b × (3a + 4b)
$\Rightarrow \frac{6ab\left(9a^2–16b^2\right)}{2ab(3a+4b)}=\frac{2\times 3\times a\times b\times (3a+4b)\times (3a–4b)}{2\times a\times b\times (3a+4b)}$
= 3 × (3a − 4b)
= 9a − 12b
$\therefore$ 6ab (9a² − 16b²) ÷ 2ab (3a + 4b) = 9a − 12b
(ii) We can factorise the given expression as
x² − 14x − 32   = x² − (16 − 2) x – 32
 = x² − 16x + 2x – 32
= x (x − 16) + 2 (x − 16)
= (x − 16) (x + 2)
$\Rightarrow \frac{x^2–14x–32}{x+2}=\frac{(x–16)(x+2)}{(x+2)}=x–16$
= x – 16
$\therefore$ (x² − 14x − 32) ÷ (x + 2) = (x − 16)
(iii) We can factorise the given expression as
36abc (5a – 25) (2b – 14) = 2 × 2 × 3 × 3 × a × b × c (5 × a – 5 × 5) (2 × b – 2 × 7)
= 2 × 2 × 3 × 3 × 5 × a × b × c (a – 5) (2 × b – 2 × 7)
= 2 × 2 × 2 × 3 × 3 × 5 × a × b × c (a – 5) (b – 7)
$\therefore \frac{36abc(5a–25)(2a–14)}{24(a–5)(b–7)}$

$=\frac{2\times 2\times 2\times 3\times 3\times 5\times \mathrm{a}\times \mathrm{b}\times \mathrm{c}(\mathrm{a}–5)(\mathrm{b}–7)}{2\times 2\times 2\times 3(\mathrm{a}–5)(\mathrm{b}–7)}=3\times 5\times \mathrm{a}\times \mathrm{b}\times \mathrm{c}=15\mathrm{abc}$
Hence, 36abc (5a − 25) (2b − 14) ÷ 24(a − 5) (b − 7) = 15abc
14.5. CORRECTING ERRORS IN RELATIONS AND SOLUTIONS OF EQUATIONS
Rajan and Sneha were asked to solve the equation 2(x − 3) = 3x + 4.
However, both of them solved the equation using different methods.
Rajan solved the equation as 2(x − 3) = 3x + 4
2x − 3 = 3x + 4
2x − 3x = 4 + 3
−x = 7
x = −7
On the other hand, Sneha solved the same equation as 2(x − 3) = 3x + 4
2x − 3x = 4 + 6
−x = 10
x = −10
Who solved the equation in the correct manner ? To find the answer, we need to check if both Rajan and Sneha attempted all the steps correctly or not.
Actually, Sneha solved the equation correctly. Rajan made a mistake in the second step, where he multiplied the expression (x − 3) with 2. He solved the second step as 2(x − 3) = 2x − 3.
We know that when an expression is multiplied with a constant or a variable, each term of the expression has to be multiplied with the constant or the variable.
However, Rajan only multiplied the term x with 2 and did not multiply the other term i.e., 3 with 2. This is the reason why his solution was incorrect.
Now, we will study some common errors that we make in Algebra.
Let us first look at the following table. In the two given columns, the same expression has been solved using two different methods. Out of the two columns containing the two methods, can you find out the correct method of solving each of the given expressions ?

Let us now look at the solution of each expression one by one.
In (i), we were required to find the value of the expression 4x, when x = −1.
4x is the product of 4 and x. Thus, we need to perform the multiplication operation on 4 and the value of x. This should not be confused with the addition or subtraction operations.
Thus, as shown in column B, when x = −1, 4x = 4(−1) = − 4.
In (ii), we were required to square the monomial 5x.
We know that we need to ensure that we square each factor of the monomial while squaring a monomial.
Thus, as shown in column A, (5x)² = (5)² × (x)² = 25x².
In (iii) and (iv), we were required to square the binomials (x − 2) and (x + 6).
We know that we should use the identities (a + b)² = a² + 2ab + b² or (a − b)² = a² − 2ab + b² while squaring a binomial.
Thus, as shown in column B, (x −2)² = (x)² − 2 × x × 2 + (2)² = x² − 4x + 4
Also, as shown in column B, (x + 6)² = (x)² + 2 × x × 6 + (6)² = x² + 12x + 36
In (v), we were required to multiply the binomials (3a − 4) and (a + 2).
We know that when we multiply two expressions, each term of the first expression has to be multiplied with each term of the second expression.
Thus, as shown in column B,
(3a − 4) (a + 2) = 3a × a + 3a × 2 − 4 × a − 4 × 2
= 3a² + 6a − 4a – 8
= 3a² + 2a – 8
In (vi), we were required to divide the expression (4x + 7) by 4.
We know that when we divide a polynomial by a monomial, we divide each term of the polynomial by the monomial.
Thus, as shown in column B, $\frac{4x+7}{4}=\frac{4x}{4}+\frac{7}{4}=x+\frac{7}{4}$
The errors that we just saw are common errors made in algebraic expressions and they should be avoided by keeping in mind the rules that we have discussed above.
Let us try and solve the following examples by eliminating the above mentioned errors.
Example 10 : Find and correct the error in the expression 2x + x + 4x = 6x.
Solution : The coefficient of the middle term (x) is 1. However, it is not shown in the expression. It should be noted that when we add the three given terms, then we also need to include the coefficient of the middle term (x).
Hence, the expression will be written as 2x + 1x + 4x = 7x.
Example 11 : Check if substituting x = −2 in x² + 2x + 6 gives (−2)² + 2 − 2 + 6 = 4 + 2 − 2 + 6 = 10.
Solution : We should use brackets while substituting a negative value.
x² + 2x + 6 = (−2)² + 2(−2) + 6 = 4 − 4 + 6 = 6
Example 12 : Find and correct the errors in the following mathematical expressions :
(i) $\frac{11{\mathrm{x}}^2}{11{\mathrm{x}}^2}=0$
(ii) (y + 8)² = y² + 64
(iii) (x + y) (x + 2y) = x² + 2y²
(iv) $\frac{12x+9}{9}=12x+1$
(v) (4x)² + 7 = 4x² + 7
(vi) 4a + 2a = 6a²
(vii) (−1)² + 4(−1) = − 1 − 4 = − 5
Solution : (i) When the dividend and the divisor are the same, the quotient is always 1.
$\frac{11x^2}{11x^2}=1$
(ii) We can find the square of a binomial using (a + b)² = a² + 2ab + b².
(y + 8)² = (y)² + 2 × y × 8 + (8)² = y² + 16y + 64
(iii) The correct expression for this problem is
(x + y) (x + 2y) = x × x + x × 2y + y × x + y × 2y = x² + 2xy + xy + 2y²
= x² + 3xy + 2y²
$\therefore$ (x + y) (x + 2y) = x² + 3xy + 2y²
(iv) When dividing a polynomial by a monomial, we divide each term of the polynomial by the monomial.
$\frac{12x+9}{9}=\frac{12x}{9}+\frac{9}{9}$
$=\frac{4\mathrm{x}}{3}+1$
$\therefore \frac{12x+9}{9}=\frac{4x}{3}+1$
(v)  The correct expression is represented as (4x)² + 7 = 16x² + 7
(vi) The correct expression is represented as 4a + 2a = 6a
(vii) The correct expression is represented as (−1)² + 4(−1) = 1 − 4 = − 3
The square of a negative number is always a positive number.