Exponents and Powers

12.1 INTRODUCTION
Exponent
If a certain number a is multiplied m times in succession, then the continued product so obtained is called the $m^{th}$ power of a and is written as $a^m$ (read as, a to the power m).
Thus, $a^m$ = a × a × a × a…….. to m factors.
Here, a is called the base of $a^m$ and m is called the index or exponent of $a^m$.
Examples
i) $x^5=x.x.x.x.x$
ii) (–3)⁶ = (–3)(–3)(–3)(–3)(–3)(–3)
Note
In particular, a² is called the square of a (or, $a^2$) and a³ is called the cube of a (or $a^3$)
Root
If a and x are two real numbers and n is a positive integer such that aⁿ = x, then a is called the $n^{th}$ root of x and is written as $a=\sqrt[n]{x} or a=x^{1/n}$
Clearly, $n^{th}$ root of x (i.e., $\sqrt[n]{x}$) is such a number whose $n^{th}$ power is equal to x i.e., $(\sqrt[n]{x}{)}^n=x$.
i) In particular, if $a^2=x$, then a is called the second root or square root of x and is written as $a=\sqrt[2]{x} or a=x^{1/2} \text{ or simply }a=\sqrt{x}$
ii) If a³ = x, then a is called the third root or cube root of x and is written as $a=\sqrt[3]{x} or a=x^{1/3}$
Examples
i) Square Root of 25 is 5 i.e., $\sqrt{25}=5 \left(\because 5^2=25\right)$
ii) Cube Root of 27 is 3 i.e., 3 $\sqrt[3]{27}=3 \left(\because 3^3=27\right)$
iii) Sixth Root of 64 is 2 i.e., 6 $\sqrt[6]{64}=2 \left(\because 2^6=64\right)$
Example
Since $5^2=25 \therefore \sqrt{25}=5$
Again, ${\left(–5\right)}^2=25 \therefore \sqrt{25}=–5$
Therefore, it is evident that both 5 and (–5) are square roots of 25.
Hence, by the Square root of a real positive number x we mean $\pm \sqrt{x}(\text{ i.e., }+\sqrt{x}\text{ or }–\sqrt{x})$
Note
i) If x > 0 and n is any positive integer, then $\sqrt[n]{x}$ is positive.
ii) If x < 0 and n is any odd integer, then $\sqrt[n]{x}$ is negative.
iii) If x < 0 and n is any positive even integer, then $\sqrt[n]{x}$ does not exist in the set of real numbers.
12.2. LAWS OF EXPONENTS
I) Multiplication property :
$a^m\times a^n=a^{m+n}\left(m, n\in z^{+}\right)$ (Fundamental Index Law)
For multiplying the power of same base, powers are added.
Proof :

$a^m\times a^n=(a\times a\times a\times \dots \dots .\text{ to }m\text{ factors})$

$\times (a\times a\times a\times a\dots \dots \text{ . to }n\text{ factors})$

$=(a\times a\times a\times a\dots ..\text{ to }(m+n\left)\text{ facors}\right)$

$\therefore a^m\times a^n=a^{m+n}$

Examples :

$\left(i\right) 2^3\times 2^4=2^{3+4}\left[\because a^m\times a^n=a^{m+n}\right]$

$\therefore 2^3\times 2^4=2^7$

$\left(ii\right) (x+y{)}^2\times (x+y{)}^3=(x+y{)}^{2+3}$

$\left[\because a^m\times a^n=a^{m+n}\right]$

$\therefore (x+y{)}^2\times (x+y{)}^3=(x+y{)}^5$

II) Division property property :

$a^m÷a^n=a^{m–n}\left(m,n\in z^{+}\right)$

For dividing the powers of same base, we subtract the indices.

Proof :

$a^m÷a^n=\frac{a^m}{a^n}=\frac{a\times a\times a\times \dots ..\text{ to }m\text{ factors }}{a\times a\times a\times \dots ..\text{ to }n\text{ factors }}$

Case – 1 : If $m>n$

$\frac{a^m}{a^n}=a\times a\times a\times a\dots \dots (m–n)\text{ factors }$

$\therefore \frac{a^m}{a^n}=a^{m–n}$

Example : $3^5÷3^2=\frac{3^5}{3^2}=3^{5–2}=3^3\left(\because \frac{a^m}{a^n}=a^{m–n}\right)$

Case –2 : If $m<n$

$\frac{a^m}{a^n}=\frac{1}{a\times a\times a\times \dots \dots (n–m)\text{ factors }}$

$\frac{a^m}{a^n}=\frac{1}{a^{(n–m)}}$

Example : $3^2÷3^5=\frac{3^2}{3^5}=\frac{3\times 3}{3\times 3\times 3\times 3\times 3}=\frac{1}{3\times 3\times 3}$

$3^2÷3^5=\frac{1}{3^3}$

III) Power of a power property :

${\left(a^m\right)}^n=a^{mn}\left(m,n\in z^{+}\right)$

Proof : ${\left(a^m\right)}^n=a^m\times a^m\times a^m\times \dots \dots \text{ to n factors }=a^{m+m+m+\dots \dots }\text{ to }n\text{ factors }$

${\left(a^m\right)}^n=a^{mn}$

Examples

i) ${\left(5^3\right)}^2=5^{3\times 2}=5^6 \left(\because {\left(a^m\right)}^n=\left(a^{mn}\right)\right)$

ii) ${\left(y^2\right)}^4=y^{2\times 4}=y^8$

$\therefore {\left(y^2\right)}^4=y^8$

IV) Power of a product property :

$a^m·b^m=(ab{)}^m \left(m,n\in z^{+}\right)$

Proof :

$a^m\times a^m=(a\times a\times a\times \dots ..\text{ to }m\text{ factors})\times (b\times b\times b\times \dots ..\text{ to }m\text{ factors})$

$=\left(ab\right)\times \left(ab\right)\times \left(ab\right)\times \dots \dots \text{ to }m\text{ facors}$

$\therefore a^m\times b^m=(ab{)}^m$

Example : $x^3·y^3=(x\times x\times x)\times (y\times y\times y)$

$=\left(xy\right)\times \left(xy\right)\times \left(xy\right)=(xy{)}^3$

$\therefore x^3.y^3=(xy{)}^3$

V) Power of a divison property :

$\frac{a^m}{b^m}={\left(\frac{a}{b}\right)}^m \left(m,n\in z^{+}\right)$

Proof : $\frac{a^m}{b^m}=\frac{a\times a\times a\times \dots \text{ to }m\text{ factors }}{b\times a\times b\times \dots \dots \text{ to }m\text{ factors }}=\frac{a}{b}\times \frac{a}{b}\times \frac{a}{b}\times \dots ..\text{ to }m\text{ factors}$

$\therefore \frac{a^m}{b^m}={\left(\frac{a}{b}\right)}^m$

all the above laws are defind for $\mathrm{m}, \mathrm{n}\in {\mathrm{z}}^{+}$ only.
12.3. NUMBERS WITH NON-INTEGER EXPONENTS
Numbers with non-integer exponents
What if m is not a positive integer ?
If m is not a positive integer, then there exist four cases.
Case-1 : either m = 0
Meaning of a° (a $\ne$ 0)
We know the Fundamental Index law being true for all indices hence,

$a°·a^m=a^{\circ +m}=a^m$

Now Dividing both sides by $a^m$ we get,

$a°=\frac{a^m}{a^m}=1(\because a\ne 0)$

Note : a° has no meaning when a = 0 i.e., 0° has no meaning.
Case-2 : Either $m=\frac{p}{q}$ where p and q are positive integers.
Meaning of $a^{p/q}$, where p and q are positive integer
Since q is a positive integer, hence,

${\left(a^{p/q}\right)}^q=a^{p/q}·a^{p/q}·a^{p/q}\dots \dots ..\text{ to q factors }$

$=a^{p/q+p/q+p/q\dots \text{ to }q\text{ factors }}=a^{p/q·q}=a^p$

$\therefore a^{p/q}=\sqrt[q]{a^p}$

Thus, $a^{p/q}$ is the $q^{th}$ root of $a^p$.
Case-3 : Either m is a negative number
Meaning of ${\mathrm{a}}^{–m}$ , where m is a positive real number and $a\ne 0$
Since the fundamental index law is true for all indices, hence,

$a^{–m}·a^m=a^{–m+m}=a°=1$

$\to a^{–m}=\frac{1}{a^m}\text{ and }\frac{1}{a^{–m}}=a^m$

Thus $a^{–m}$ is the reciprocal of $a^m$.

Case-4 : Either $m=–\frac{p}{q}$ where, p and q are positive integers.
We have, $a^{–p/q}=\frac{1}{a^{p/q}}=\frac{1}{\sqrt[q]{a^p}}$

Equations and identities involving Indices

If a, m, n are three real numbers and $a^m=a^n,\text{ then }m=n(a\ne 0,1,\infty )$
Proof : Since $a^m=a^n\text{ and }a\ne 0,1,\infty \text{ hence, }\frac{a^m}{a^n}=1\text{ or }{a}^{m–n}=a°$

$\therefore m–n=0\Rightarrow m=n\text{ proved}$

12.4. RATIONAL EXPONENT

I) Rational Number

The fraction $\frac{p}{q}$where p and q are integers, $q\ne 0$ is called a rational number.

II) Positive Rational Exponent

Let a be a positive real number and n a positve fraction equal to $\frac{p}{q},\text{ i.e., }n=\frac{p}{q}$ where p and q are positive integers, the equation $x^q=a^p$ has one and only positive solution for x, given by $x=a^{\frac{p}{q}}=\sqrt[q]{a^p}=q^{th}\text{ root of }{a}^p$.

III) Negative Rational Exponent

If n is a negative rational, i.e. $n=–\frac{p}{q}$, where $q\ne 0$ and a is a positive real number, then $a^n=a^{\frac{p}{q}}=\frac{1}{a^{\frac{p}{q}}}$

Consider, $x^{–\frac{p}{q}}=\frac{1}{x^{\frac{p}{q}}}\left[\because x^{–m}=\frac{1}{x^m}\right]={\left(\frac{1}{x}\right)}^{\frac{p}{q}}$

$x^{–\frac{p}{q}}\text{ is the reciprocal of }{x}^{\frac{p}{q}}$

$\text{Thus, if }x=\frac{r}{s}\left(r,s>0\right),\text{ then }{\left(\frac{r}{s}\right)}^{\frac{p}{q}}={\left(\frac{s}{r}\right)}^{\frac{p}{q}}$

$\therefore {\left(\frac{r}{s}\right)}^{–m}={\left(\frac{s}{r}\right)}^m\text{ where }m\in Q$

IV) Also, all the laws of indices applicable for integral index are also applicable for rational index.
i.e., if a is a positive real number and m, n are rational numbers, then,

i) $a^m\times a^n=a^{m+n}$

ii) ${\left(a^m\right)}^n=a^{mn}$

iii) $(ab{)}^m=a^m{b}^m$

12.5. RADICAL AND RADICAND

We know that if $y>0\text{ and }{y}^{\frac{1}{q}}=x,$ then we can write it as $x= \sqrt[q]{y}$

Here, $\sqrt[q]{\mathrm{y}}$ y is called ‘Radical form’ of $y^{\frac{1}{q}}$

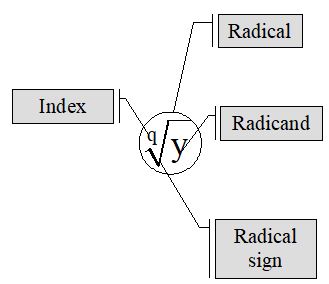
i) In $\sqrt[q]{y}, \sqrt{}$ is called Radical Sign
ii) $\sqrt[q]{y}$ is called a Radical
iii) q is called Index of the radical
iv) y is called the Radicand
Note : Index of a radical is always positive
Important Results
i) $\sqrt[n]{a^n}=a$
ii) $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$
iii) $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
iv) $\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
v) $\sqrt[n]{a^{–m}}=a^{–\frac{m}{n}}$