11.1 INTRODUCTION
We have learnt that for a closed plane figure, the perimeter is the distance around its boundary and its area is the region covered by it. We found the area and perimeter of various plane figures such as triangles, rectangles, circles etc. We have also learnt to find the area of pathways or borders in rectangular shapes.
In this chapter, we will try to solve problems related to perimeter and area of other plane closed figures like quadrilaterals. We will also learn about surface area and volume of solids such as cube, cuboid and cylinder.
11.2 BASIC CONCEPTS
Closed Figure
A figure with no open ends is a closed figure.
Regular closed figures: A closed figure in which all the sides and angles equal.
Perimeter
Perimeter is the distance covered along the boundary forming a closed figure when we go round the figure once. The concept of perimeter is widely used in real life.
Example
• For fencing land.
• For building a compound wall around a house.
The perimeter of a regular closed figure is equal to the sum of its sides.
Perimeter of a Rectangle
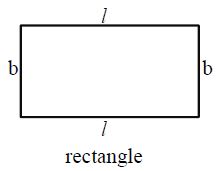
= Length (l) + Breadth (b) + Length (l) + Breadth (b) = 2(l + b)
Perimeter of a Square
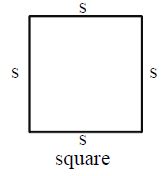
= s + s + s + s
= 4 × s
Equilateral Triangle
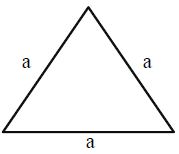
A triangle with all its sides and angles equal is called an equilateral triangle.
The perimeter of an equilateral triangle with the side ‘a’ = a + a + a
= 3 × a
Area
The amount of surface enclosed by a closed figure is called its area. The following conventions are to be adopted while calculating the area of a closed figure using a squared or graph paper.
1. Count the fully-filled squares covered by the closed figure as one square unit or unit square each.
2. Count the half-filled squares as half a square unit.
3. Count the squares that are more than half-filled as one square unit.
4. Ignore the squares filled less than half.
For example, the area of this shape can be calculated as shown: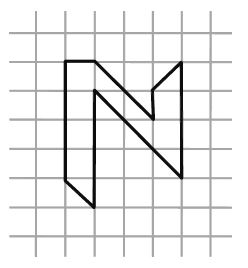
|
Covered area |
Number |
Area estimate (sq. units) |
|
Fully filled squares |
6 |
6 |
|
Half-filled squares |
6 |
|
|
Squares filled more than half |
0 |
0 |
|
Squares filled less than half |
0 |
0 |
Area covered by full squares = 6 × 1 = 6 sq. units Area covered by half squares = 7 × ½ = 7/2= 3 ½ sq. units
Total area of the given shape = 6 + 3 ½ sq. units Thus, the total area of the given shape = 9 ½ sq. Units
Area of a rectangle can be obtained by multiplying length by breadth. Area of the square can be obtained by multiplying side by side.
Perimeter and Area of Some specific Triangles and Quadrilaterals
Triangle
The closed figure obtained by joining three non collinear points is called a triangle.
Let a, b, c lengths of sides triangle then s = a + b + c is a perimeter of triangle, is called semi perimeters of the triangle
Equilateral Triangle
A triangle which is having equal sides is called an equilateral triangle.
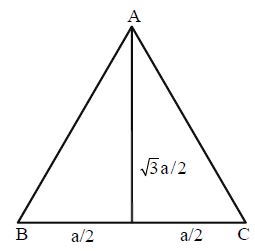
Let the side of an equilateral triangle be ‘a’ then height of equilateral triangle
Perimeter of equilateral triangle = 3a units.
Right Angle Triangle
In a triangle ABC if one angle is , then it is called a right angled triangle
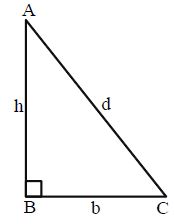
Note: If ABC is a Right Angled Triangle then by Pythagoras Theorem
(Hypotenuse)2 = (Side)2 + (Side)2
Perimeter of right angled triangle = b + h + d
Acute-Angle Triangle
The triangle which is having all angles less than is called an acute angle triangle.
Obtuse Angled Triangle
In a triangle one angle is above , then it is called an obtuse angle triangle.
Quadrilaterals
Rectangle
The quadrilateral which is having pair of equal and parallel opposite sides and one angle is .
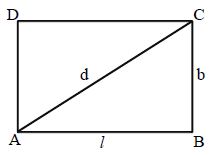
Let ABCD be a rectangle of length = l units, breadth = b units, diagonal = d units.
• Perimeter of the rectangle = 2(l + b) units
• Area = l × b units
• Area (A) =
• Diagonal (d) =
Square
The rectangle which is having all sides equal, all angles are right angles is called Square.
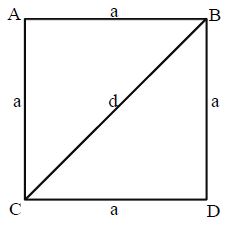
Let the side length of a square be ‘a’ units, then
• Perimeter of square = 4a units
• Diagonal of the square = units
• Area of the square = a2 sq.units
• Area of the square = × (diagonal )2 = d2 sq.units, where ‘d’ is length of diagonal
• Side of square = units
|
Length Units |
Area Units |
|
1 cm = 10 mm |
1 cm2 = (10 × 10)mm2 = 100 mm2 |
|
1 m = 100 cm |
1 m2 = (100 × 100)cm2= 1000 cm2 |
|
1 dam= 10 m |
1 dam2 = (10 × 10)m2 = 100 m2 = 1 Are |
|
1 hm = 100 m |
1 hm2 = (100 × 100)m2 = 10000 m2 =1hectare |
Rectangular paths
The path obtained between outer rectangular and inner rectangular fields is called Rectangular path.
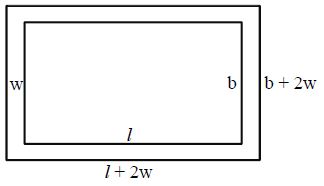
If ‘l’, ‘b’ are length and breaths of inner rectangle and ‘w’ be width of path then
• Length of outer rectangle = l + 2w
• Breadth of outer rectangle = b + 2w
• Area of inner rectangle = lb
• Area of outer rectangle = (l + 2w) (b + 2w)
• Area of path = (l + 2w) (b + 2w) – lb = 2(l + b)w + 4w2
Perimeter and Area of Circle
A circle is defined as a collection of points on a plane that are at an equal distance from a fixed point on the plane. The fixed point is called the centre of the circle.
Circumference
The distance around a circular region is known as its circumference.
Diameter
Any straight line segment that passes through the centre of a circle and whose end points are on the circle is called its diameter.
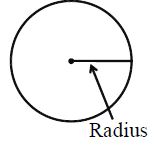
Radius
Any line segment from the centre of the circle to its circumference.
Circumference of a circle = 2r , Circumference of a circle = d, where r is the radius of the circle or, where d is the diameter of the circle.
is an irrational number, whose value is approximately equal to 3.14.
Circumference = Diameter x 3.14
Diameter(d) is equal to twice radius(r): d = 2r
Circles with the same centre but different radii are called concentric circles.
The area of a circle is the region enclosed in the circle.
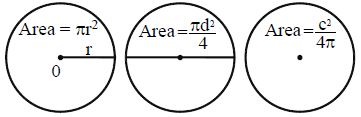
The area of a circle can be calculated by using the formula:
r2 , if radius r is given
, if diameter D is given ( )
, if circumference C is given
11.3 AREA OF TRAPEZIUM
Let ABCD be a trapezium.
Base: Each of the two parallel sides of trapezium is called a base of the trapezium
Altitude (or) height: The distance between the two parallel sides (bases) is called Altitude or height.
In the figure, diagonal AC divides the trapezium ABCD into ABC and ADC
Area of trapezium = (Area of ABC) + (Area of ADC) ________ (1)
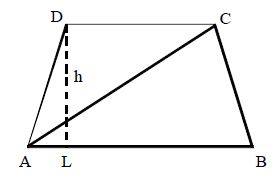
Area of ABC =
Area of ACD =
Area of trapezium ABCD
(sum of parallel sides)(distance of parallel sides)
Perimeter of trapezium = sum of all the sides = (AB + BC + CD + DA) cm.
11.4 AREA OF A GENERAL QUADRILATERAL
Let ABCD be an quadrilateral.
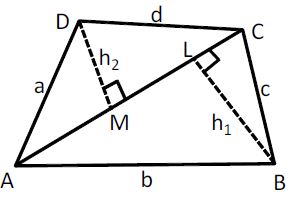
BL = = Altitude (perpendicular)
DM = = Altitude (perpendicular)
Area of Quadrilateral
(length of diagonal) (sum of lengths of perpendiculars)
Area of special quadrilaterals
Let ABCD be a rhombus.
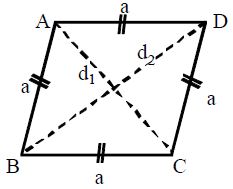
AB = BC = CD = DA = a cm
AC = cm = diagonal
BD = cm= diagonal
Area of Rhombus = (product of diagonals)
Perimeter of Rhombus = sum of all the sides
= a + a + a + a = 4a cm
11.5 AREA OF A POLYGON
1. Area of a Regular Polygon
Case-1: Area of regular polygon in terms of its side and radius of the inscribed circle.
Let ‘G’ and ‘H’ be any two vertices of a regular polygon
Let ‘O’ be the centre of the inscribed circle.
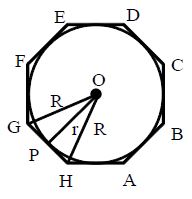
OG and OH be the bisectors and OP be the perpendicular drawn from O to GH, Then OP = r (in-radius) We will also get the polygon divided into n equal triangles like OGH.
Area of polygon = Area of OGH × Number of sides of the polygon
(each side = a units)
sq.units
Area of regular polygon
= perimeter × in-radius ( perimeter of a polygon of n sides, each of length a units = na)
= (na)r.unit
Case-2: Area of regular polygon in terms of the radius of the circumscribed circle.
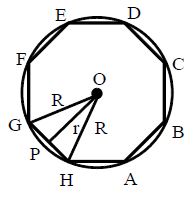
From the figure, we have OP = r and circum radius = OA = R,
let GH = a units.
From the right-angled triangle POH, we have
(OH)2 = (OP)2 + (PH)2 [ by Pythagoras theorem)
Area of the polygon = sq. units
2. Area of a Regular Hexagon
Case-1: Let ABCDEF be a regular Hexagon with OP as its in-radius (r) and the length of each side = a.
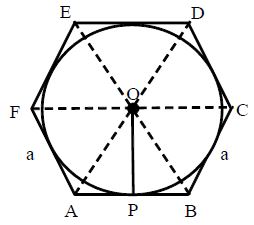
Area of the Hexagon = 6 × area of ?OAB
(DOAB is an equilateral triangle)
Case-2:
Let ABCDEF be the hexagon with OA = r as radius and length of each side = a.
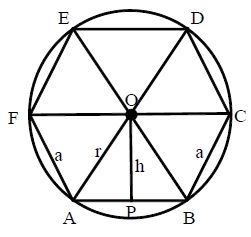
Let OP = b be the perpendicular drawn from centre O to AB.
From equilateral triangle AOB,
Area
Area of hexagon = = 3ah sq. units.
3. Area of an Octagon
Let ABCDEFGH be the given Octagon, O the in- centre, and OP = r and length of each side = a.
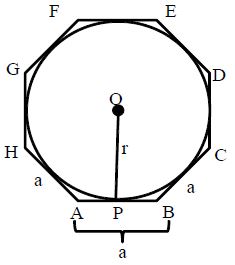
The area of a regular Octagon
11.6 SOLID SHAPES
Wherever we look, we usually see solids. So far, in all our study, we have been dealing with figures that can be easily drawn on our notebooks or blackboards. These are called plane figures. We have understood what rectangles, squares and circles are, what we mean by their perimeters and areas, and how we can find them. We have learnt these in earlier classes. It would be interesting to see what happens if we cut out many of these plane figures of the same shape and size from a cardboard sheet and stack them up in a vertical pile. By this process, we shall obtain some solid figures (briefly called solids) such as a cuboid, a cylinder, etc. In the earlier classes, you have also learnt to find the surface areas and volumes of cuboids, cubes and cylinders. We shall now learn to find the surface areas and volumes of cuboids and cylinders in details and extend this study to some other solids such as cones, spheres, prisms, pyramids.
Before, go into details, let us know what are solids.
The bodies that have three dimensions in space are called solids. For example, a block of wood which has three dimensions – length, breadth and height – is a solid. The space occupied by a solid body is called its volume.
The common units of volume are cubic centimetres (cm3) or cubic metre (m3). The different solids that we are going to know in this chapter are:
11.7 VOLUME AND SURFACE AREA OF CUBE AND CUBOID
A solid bounded by six rectangular plane faces is called cuboid.
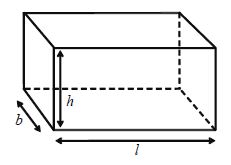
Let the Dimensions of cuboid be length = ‘l’ units, breath = ‘b’ units, height = ‘h’ units, then
• Diagonal of cuboid = units
• Total surface Area of cuboid
= 2(lb + bh + lh) sq units
• Lateral surface Area of cuboid
= 2 (l × b)× h sq. units
• Volume of cuboid = lbh cubic units
• Area of 4 walls of room = 2 (l × b)× h sq.units
Volume and Surface area of Cube
The cuboid whose length breath and height are equal is called a cube.
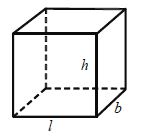
Let the edge of a cube be ‘a’ units then
• Diagonal of cube = a units
• Total surface Area of cube = 6a2 square units
• Lateral surface Area of cube = 4a2 square units
• Volume of cube = a3 cubic units.
11.8 VOLUME AND SURFACE AREA OF CYLINDER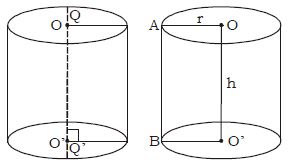
1. A solid like measuring jars, circular pillars, circular pipes etc., is called a cylinder.
2. Cylinders have a curved (also called lateral) surface with congruent circular ends.
3. The line joining the centres of the circular ends of a cylinder is called its axis.
4. If it is perpendicular to the circular ends, then it is called a right circular cylinder.
Here, by the word cylinder we will mean the right circular cylinder.
A right circular cylinder, may also be considered as a solid generated by the revolution of a rectangle about one of its sides. Thus, if a rectangle OO ‘ BA revolves about its side OO ‘ and completes one revolution to arrive at its initial position, a right circular cylinder will be generated whose axis is OO ‘ and radius AO = BO ‘ = r(say). The length of the axis OO ‘ between the centres is called the length or the height (h) of the cylinder.
Area of Curved Surface of Cylinder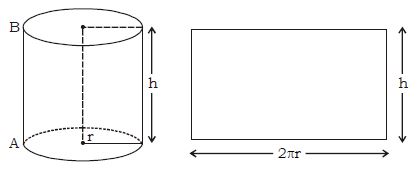
This cylinder has a circular base of radius r cm and a height of h cm. Its surface area is made up of the curved surface area plus the areas of the circular top and base.
If it is a paper cylinder and you cut it through the line AB, and spread this paper on a plane you will get a rectangle whose length will be equal to the circumference of the base of the cylinder, i.e., 2r and width equal to AB, i.e., h
Area of the curved surface = area of the rectangle = 2rh
The area of the circular base and top are both equal to r2. So the combined area of the top and base is 2r2.
So the total surface area of the cylinder = 2rh + 2r2
Lateral Surface of a Hollow Cylinder
Let be external radius and internal radius then
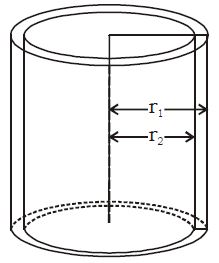
Curved surface of the hollow cylinder
= sum of the curved surface of both the cylinders
Total surface area of the hollow cylinder
= curved surface of the hollow cylinder + sum of the areas of the rings at the ends
= =
=
=
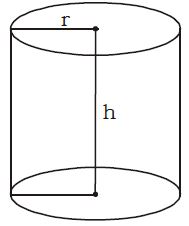
Volume of a Cylinder
Volume of a cylinder = (Area of the base) = height = (r2 )h
Volume of a cylinder = r2h
Volume of the Material of a Hollow Cylinder
If the outer and inner radii of a hollow cylinder of height h volume of the material composing the cylinder arc R and r respectively, then the volume of the material composing the cylinder.
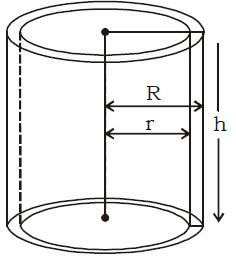
= External volume – Internal volume
= R2h – r2h – h(R2 – r2 )
=








