Symmetry

1. REFLECTION SYMMETRY OR LINEAR SYMMETRY
Consider the following figures 

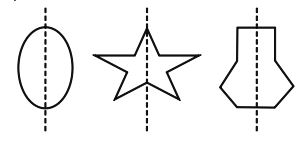
Clearly, if each of these figures is folded along the dotted line, then the pair of the figure on one side of the dotted line falls exactly over the other part i.e., in each figure, the dotted line divides the figure into two coincident parts called the mirror images of each other. Such figures are said to posses linear symmetry or reflection symmetry.

Thus, we define: If a line divided a given figure into two coincidental parts, then we say that the figure is symmetrical about the line and the line is called the axis of symmetry or line of symmetry.
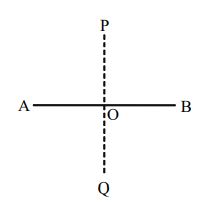
Eg: A line segment (say AB) is symmetrical about its perpendicular bisector (say PQ) as shown in the below figure

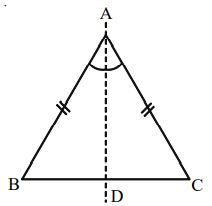
An isosceles triangle ABC is symmetrical about the bisector AD of the angle included between the equal sides

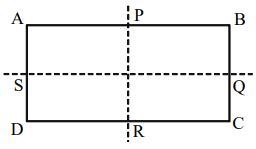
A rectangle has two lines of symmetry, each one of which is the line joining the mid-points of opposite sides. In the figure, the rectangle ABCD is symmetrical about the lines PR&QS

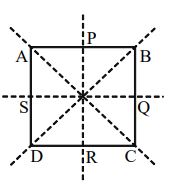
A square has four lines of symmetry- its two diagonals and the line joining the mid-points of its opposite sides.

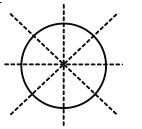
A circle has an infinite number of lines of symmetry- each one of its diameter is a line of symmetry.

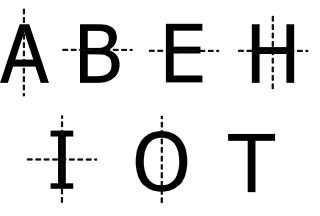
Note: The following letters of the English alphabet have one or more line of symmetry:

2. POINT SYMMETRY
A figure is said to be symmetric about a point ‘O’ called the centre of symmetry. If corresponding to each point ‘P’ on the figure, there exists a point ‘P’ on the other side of centre, which is directly opposite to the point ‘P’ and lies on the figure.
Note: A figure that possess a point symmetry regains its original shape even after being rotated through ${180}^0$.
Eg: The capital letter ‘S’ of the English alphabet also possesses a point symmetry as shown: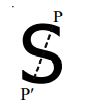

Clearly, for any point ‘P’ on the figure, there exists a point P’ on the figure, which lies directly opposite to ‘P’ such that $\mathrm{OP}={\mathrm{OP}}^{\mathrm{\prime }}$. Also the figure retains its original shape when rotated through ${180}^0$.

3. ROTATIONAL SYMMETRY
A figure is said to possess a rotational symmetry if it fits onto itself more than once while being rotated through ${360}^0$ . If $A^0$ is the smallest angle by which a particular figure has to be rotated so that its rotated from fits onto the original form, then the order of rotational symmetry is given by $\frac{{360}^0}{A}$.
For a figure to possess a rotational symmetry, we must have ${\mathrm{A}}^{\circ }\le {180}^{\circ }$. Thus, the order of rotational symmetry of a figure may be defined as the number of times the figure fits onto itself in the process of rotational through ${360}^0$.
Eg: While rotating the following figure through ${360}^0$ about the point ‘O’(mid-point of BC), it attains the original form twice (upon rotating through ${180}^0$ and ${360}^0$) as shown below:

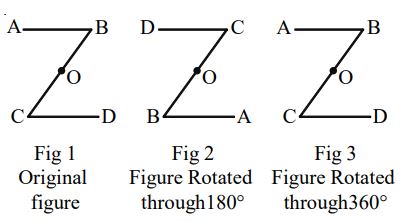
Clearly, the above figure (fig. 1) possesses rotational symmetry of order 2.
If an equilateral triangle ABC is rotated through ${360}^0$ about the point ‘O’ (point of intersection of angle bisectors), it attains the original form three time (upon rotation through ${120}^{\circ },{240}^{\circ }\text{ and }{360}^{\circ }$) as shown below:

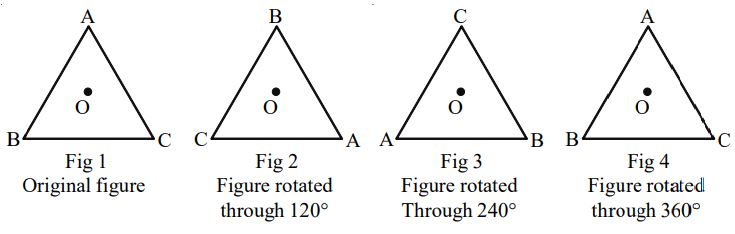
Clearly, the above figure (Fig. 1) possesses a rotational symmetry of order 3.

4. THREE TYPES OF SYMMETRIES FOR VARIOUS GEOMETRICAL FIGURES
A Line Segment AB

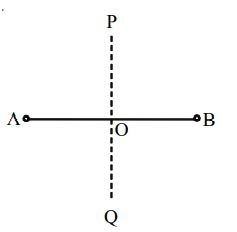
Linear Symmetry: One line of symmetry i.e., the perpendicular bisector PQ of the line segment.
Point Symmetry: Possesses a point symmetry having the midpoint ‘O’ of the line segment as the center of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 2 about the mid-point ‘O’ of the line segment.
An Angle AOB having equal Arms OA and OB

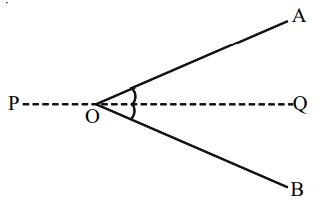
Linear Symmetry: One line of symmetry i.e., the bisector PQ of the angle.
Point Symmetry: No point symmetry
Rotational Symmetry: No rotational symmetry
An Equilateral Triangle ABC

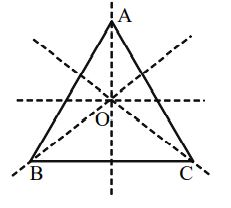
Linear Symmetry: Three lines of symmetry i.e. the bisector of the three interior angles.
Point Symmetry: No point symmetry
Rotational Symmetry: Possesses a rotational symmetry of order 3 about the point of intersection ‘O’ of the bisector of the interior angles.
An Isosceles Triangle ABC having AB = BC

Linear Symmetry: One line of symmetry i.e., the bisector PQ of the angle included between equal sides.
Point Symmetry: No point symmetry
Rotational Symmetry: No rotational symmetry
A Scalene Triangle ABC

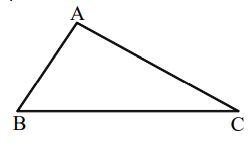
Linear Symmetry: No linear symmetry
Point Symmetry: No point symmetry
Rotational Symmetry: No rotational symmetry
A Square ABCD

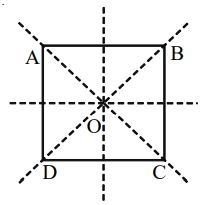
Linear Symmetry: Four lines of symmetry i.e., its two diagonals and the two lines each joining the midpoint of the opposite sides of the square.
Point Symmetry: Possesses a point symmetry with the point of intersection ‘O’ of its diagonals as the centre of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 4 about the point of intersection ‘O’ of its diagonals.
A Rhombus ABCD

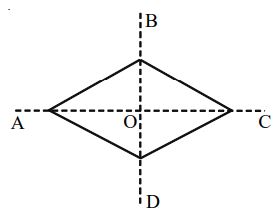
Linear Symmetry: Two lines of symmetry i.e., its two diagonals
Point of Symmetry: Possesses a point symmetry with the point of intersection ‘O’ of its diagonals as the centre of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 2 about the point of intersection ‘O’ of its diagonals.
A Rectangle ABCD

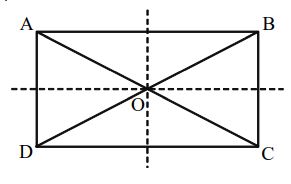
Linear Symmetry: Two lines of symmetry each of which is a line joining the mid-points of two opposite sides of the rectangle.
Point of Symmetry: Possesses a point of symmetry with the point of intersection ‘O’ of its diagonals as the centre of symmetry
Rotational Symmetry: Possesses a rotational symmetry of order 2 about the point of intersection ‘O’ of its diagonals.
A Parallelogram ABCD

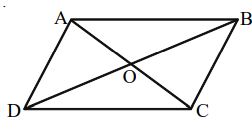
Linear Symmetry: No linear symmetry
Point of Symmetry: Possesses a point of symmetry with the point of intersection ‘O’ of its diagonals as the center of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 2 about the point of intersection ‘O’ of its diagonals.
An Isosceles Trapezium ABCD in which BC = DA and AB || DC

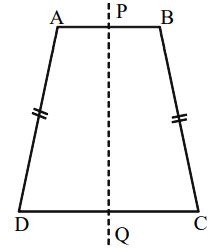
Linear Symmetry: One line of symmetry i.e., line PQ joining the mid-points of the parallel sides AB and DC of the trapezium.
Point Symmetry: No point symmetry.
Rotational Symmetry: No rotational symmetry.
A Kite ABCD in which AB = BC and CD = DA

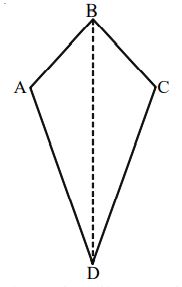
Linear Symmetry: One line of symmetry i.e., the diagonal BD.
Point Symmetry: No point symmetry.
Rotational Symmetry: No rotational symmetry.
A Semi-Circle having diameter AB

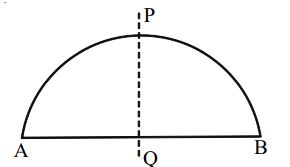
Linear Symmetry: One line of symmetry i.e., the perpendicular bisector of the diameter AB.
Point Symmetry: No point symmetry.
Rotational Symmetry: No rotational symmetry.
A Regular Pentagon

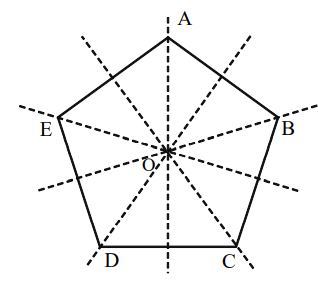
Linear Symmetry: Five lines of symmetry each being the perpendicular bisector of a side of the pentagon.
Point Symmetry: No point symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 5 about the point ‘O’ of intersection of the perpendicular bisectors of the sides of the pentagon.
A Regular Hexagon

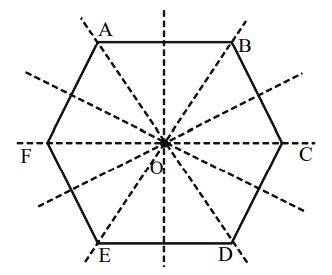
Linear Symmetry: Six lines of symmetry i.e., three diagonals passing through the centre ‘O’ and three lines joining the mid-points of the opposite sides of the hexagon.
Point Symmetry: Possesses a point symmetry with the centre ‘O’ of the hexagon as the centre of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of order 6 about the centre ‘O’ of the hexagon.
A Circle with Centre ‘O’

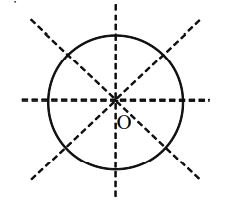
Linear Symmetry: An infinite number of lines of symmetry i.e., all possible diameter of the circle.
Point Symmetry: Possesses a point symmetry with its centre ‘O’ as the centre of symmetry.
Rotational Symmetry: Possesses a rotational symmetry of an infinite order about the centre ‘O