Rational Numbers

1. INTRODUCTION
The word ‘rational’ is derived from the word ‘ratio.
A rational number is any number that can be named in the form $\frac{a}{b}$ where a and b are integers and $b\ne 0$.

Thus, each of the numbers $\frac{5}{6},\frac{-6}{11},\frac{-13}{9},\frac{6}{-17}$ is a rational number.

Note:
1. Every natural number is a rational number but a rational number need not be a natural number.
We can write  $1=\frac{1}{1},2=\frac{2}{1},3=\frac{3}{1}$and so on.

This shown that every natural number n can be written as $\frac{n}{l}$ which is a rational number.
But none of the rational numbers like $\frac{5}{6},\frac{3}{8},\frac{1}{3},\text{ etc. }$is a natural number

2. Zero is a rational number.
We can write 0 in anyone of the forms $\frac{0}{1},\frac{0}{-1},\frac{0}{2},\frac{0}{-2},\frac{0}{3},\frac{0}{-3}$and so on. Thus, 0 can be expressed as $\frac{p}{q}$ , where p = 0 and q is any non-zero integer. Hence, 0 is a rational number.

3. Every integer is a rational number but a rational number need not be an integer.
We know that $1=\frac{1}{1},2=\frac{2}{1},3=\frac{3}{1},-1=\frac{-1}{1},-2=\frac{-2}{1},-3=\frac{-3}{1}$ and so on.
In general, any integer n can be written as $n=\frac{n}{l}$which is a rational number.
But rational numbers like $\frac{5}{7},\frac{-7}{8},\frac{11}{-6}$ are not integers

4. Every fraction is a rational number but a rational number need not be a fraction.

Let $\frac{p}{q}$ by any fraction. Then p and q are natural numbers. Since every natural number is an integer, therefore, p and q are integers.
Thus, the fraction $\frac{p}{q}$ is the quotient of two integers such that $q\ne 0$ .
Hence, $\frac{p}{q}$ is a rational number.

Numerator and Denominator
Let $\frac{p}{q}\left(q\ne 0\right)$ be a rational number. It has two terms. One is p above the line ‘____’ and the other is q below the line.
p is called the numerator of the rational number and q is called the denominator.

Positive and Negative Rational Numbers
1. A rational number is said to be positive if its numerator and denominator are either both positive or both negative.
For example $\frac{5}{7},\frac{29}{18},\frac{-6}{-19},\frac{-27}{-83}$ are all positive rational numbers.
2. A rational number is said to be negative if its numerator and denominator are such that one of them is a positive integer and the other is a negative integer.
For example, Each of the numbers $\frac{-7}{9},\frac{28}{-59},\frac{-37}{11},\frac{56}{-217}$ is a negative rational numbers.
Note:
1. Every negative integer is a negative rational number.
Example., –1, –2, –3 and so on, which may be expressed as $-1=\frac{-1}{1},-2=\frac{-2}{1},-3=\frac{-3}{1}\dots$are all negative rational numbers.
2. The rational number 0 is neither positive nor negative.

Two Important Properties of Rational Numbers
Property 1
Equivalent rational numbers

If $\frac{p}{q}$is a rational number and m is a non-zero integer, then $\frac{p}{q}=\frac{p\times m}{q\times m}$

$\text{ Thus, }\frac{-3}{4}=\frac{(-3)\times 2}{4\times 2}=\frac{(-3)\times 3}{4\times 3}=\frac{(-3)\times 4}{4\times 4}=\frac{(-3)\times 5}{4\times 5}=\dots \dots$

$\text{ i.e., }\frac{-3}{4}=\frac{-6}{8}=\frac{-9}{12}=\frac{-12}{16}=\frac{-15}{20}= .....$

All these rational numbers are equal to one another and are called equivalent rational numbers.
Property 2
Reducing to a simpler form

If $\frac{p}{q}$is a rational number and m is a common divisor of p and q then $\frac{p}{q}=\frac{p÷m}{q÷m}$

$\begin{array}{l}\frac{-48}{60}=\frac{-48:2}{60÷2}=\frac{-24}{30},\frac{-48}{60}=\frac{-48÷6}{60÷6}=\frac{-8}{10}\\ \frac{-48}{60}=\frac{-48÷12}{60÷12}=\frac{-4}{5}\end{array}$

The rational number $\frac{–4}{5}$ is in lowest terms.

2. RATIONAL NUMBERS IN STANDARD FORM
A rational number is said to be in standard form if its denominator is positive and it is in the lowest terms.
To express a given rational number in standard form, proceed as under:
Step1. If not already so, make the denominator of the given rational number positive.
Step2. Divide both the numerator and the denominator by their HCF.
3. RATIONAL NUMBERS ON A NUMBER LINE
In Class VI, you have learnt how to represent integers on a number line.
If you draw any line as shown below, take a point O on it which you may call the zero point, set off equal distances on both sides of O on the line, then these distances will be considered as of unit length.
If we name the points on the right as A, B, C, D, E, …… and the corresponding points on the left as $A‘, B‘, C‘, D‘, E‘$,…..

Then A, B, C, D, E, …. will represent the points 1, 2, 3, 4, 5, ….       and

$A‘, B‘, C‘, D‘, E‘$,…. Will represent the points –1, –2, –3, –4, –5….

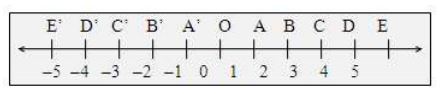
In the same manner as done, we can represent rational numbers on a number line and obtain a rational number line.

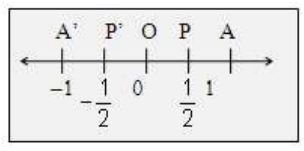
(i) If we bisect OA, we get the point P which represent the rational number $\frac{1}{2}$ . Similarly, if we bisect OA’ , we get the point P’ which represents the rational number $–\frac{1}{2}$

(ii) If we divide the lengths OA and OA’ into three equal parts and label the points of division as P, Q, P’, Q’ as shown,

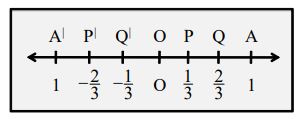
then P, Q will represent the rational numbers $\frac{1}{3}\text{ and }\frac{2}{3}$respectively. Likewise, points P’, Q’ will
represent the rational numbers $–\frac{1}{3}\text{ and }–\frac{2}{3}$ respectively.

4. COMPARISON OF RATIONAL NUMBERS
There are two ways to compare Rational numbers:
• Number Line
• Arithmetical Process1 8 Mathematics
Number Line
One can compare rational numbers by using a number line easily. Arrange the rational numbers on the number line in ascending order from left to right.
Example: The Rational numbers having 4 as denominator can be represented on the number line as follows. Of the two rational numbers represented on the number line, the number on the left is smaller than the number to its right, Thus

$\begin{array}{l}-\frac{3}{4}<\frac{7}{4},\frac{3}{4}<\frac{7}{4}\\ -\frac{7}{4}<-\frac{5}{4},-\frac{3}{4}>-\frac{5}{4}\dots \end{array}$

We observe from the above example that:
• A positive rational number is always greater than a negative rational number.
• Zero is greater than each one of the negative rational numbers and less than each one of the
positive rational numbers.
Arithmetical Process
• Express each rational number with a positive denominator.
• Find L.C.M of the positive denominators.
• Express each of the given rational numbers with L.C.M as the common denominator.

$\begin{array}{l}\text{ Thus, }\frac{2}{5},\frac{4}{3}\\ \frac{2}{5}=\frac{2}{5}\times \frac{3}{3},\frac{4}{3}=\frac{4}{3}\times \frac{5}{5}\\ \frac{6}{15},\frac{20}{15}\\ \frac{6}{15}<\frac{20}{15}\end{array}$

• The number having greater numerator is greater.
• A positive rational number is always greater than a negative rational number
• Zero is greater than each one of the negative rational numbers and less than each one of the
positive rational numbers.
5. RATIONAL NUMBERS BETWEEN TWO RATIONAL NUMBERS
Can you tell the natural numbers between 1 and 5? They are 2, 3 and 4.
How many natural numbers are there between 7 and 9? There is one and it is 8.
How many natural numbers are there between 10 and 11? Obviously none.
List the integers that lie between –5 and 4. They are – 4, – 3, –2, –1, 0, 1, 2, 3.
How many integers are there between –1 and 1?
How many integers are there between –9 and –10?
You will find a definite number of natural numbers (integers) between two natural numbers (integers).
How many rational numbers are there between $\frac{3}{10}\text{ and }\frac{7}{10}?$

You may have thought that they are only $\frac{4}{10},\frac{5}{10}\text{ and }\frac{6}{10}$ .

But you can also write $\frac{3}{10}\text{ as }\frac{30}{100}\text{ and }\frac{7}{10}\text{ as }\frac{70}{100}$ .

Now the numbers, $\frac{31}{100},\frac{32}{100},\frac{33}{100},\dots ..\frac{68}{100},\frac{69}{100}$, are all between $\frac{3}{10}\text{ and }\frac{7}{10}$.

The number of these rational numbers is 39.

Also $\frac{3}{10}$ can be expressed as $\frac{3000}{10000}\text{ and }\frac{7}{10}\text{ as }\frac{7000}{10000}$.

Now, we see that the rational numbers $\frac{3001}{10000},\frac{3002}{10000},\dots \dots ,\frac{6998}{10000},\frac{6999}{10000}$are between $\frac{3}{10}\text{ and }\frac{7}{10}$.

These are 3999 numbers in all. In this way, we can go on inserting more and more rational numbers between $\frac{3}{10}\text{ and }\frac{7}{10}$.So unlike natural numbers and integers, the number of rational numbers between two rational numbers is not definite. Here is one more example.
How many rational numbers are there between $\frac{-1}{10}\text{ and }\frac{3}{10}?$

Obviously $\frac{0}{10},\frac{1}{10},\frac{2}{10}$ are rational numbers between the given numbers.

If we write $\frac{-1}{10}\text{ as }\frac{-10000}{100000}\text{ and }\frac{3}{10}\text{ as }\frac{30000}{100000}$,

we get the rational numbers $\frac{-9999}{100000},\frac{-9998}{100000}, \dots ..$

$\frac{-29998}{100000},\frac{-29999}{100000}\text{ between }\frac{-1}{10}\text{ and }\frac{3}{10}.$

You will find that you get countless rational numbers between any two given rational numbers.

6. OPERATIONS ON RATIONAL NUMBERS
You know how to add, subtract, multiply and divide integers as well as fractions. Let us now study these basic operations on rational numbers.
Addition
Let us add two rational numbers with same denominators, say $\frac{7}{3}\text{ and }\frac{-5}{3}$.

$\text{ We find }\frac{7}{3}+\left(\frac{-5}{3}\right)$

On the number line, we have:

The distance between two consecutive points is $\frac{1}{3}$. So adding $\frac{–5}{7}to\frac{7}{3}$ will mean, moving to the left of $\frac{7}{3}$, making 5 jumps. Where do we reach? We reach at $\frac{2}{3}$.

$\text{ So, }\frac{7}{3}+\left(\frac{-5}{3}\right)=\frac{2}{3}\text{ . }$

Subtraction
Difference of two rational numbers $\frac{–3}{5}$by 2, i.e,. we find $\frac{–3}{5}\times 2$ .

On the number line, it will mean two jumps of $\frac{3}{5}$ to the left.

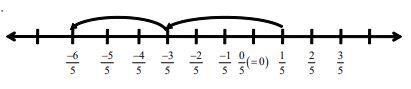
Where do we reach? We reach at $\frac{–6}{5}$ .

Let us find it as we did in fractions. $\frac{-3}{5}\times 2=\frac{-3\times 2}{5}=\frac{-6}{5}$

Division
We have studied reciprocals of a fraction earlier. What is the reciprocal of $\frac{2}{7}$ ? It will be $\frac{7}{2}$. We extend this idea of reciprocals to rational numbers also.
The reciprocal of $\frac{–2}{7}$will be $\frac{7}{–2}$; that of $\frac{–3}{5}$would be $\frac{–5}{3}$.

Dividing a rational number $\frac{4}{9}$ by another rational number $\frac{–5}{7}$as, $\frac{4}{9}÷\frac{-5}{7}=\frac{4}{9}\times \frac{7}{-5}=\frac{-28}{45}$ .

7. PROPERTIES OF RATIONAL NUMBERS
Addition on rational numbers satisfies the closure property, the commutative law and the associative law.
Zero is the identity element for the addition of rational numbers.
Every rational number $\frac{p}{q}$ has its additive inverse $\frac{–p}{q}$.
Multliplication on rational numbers satisfies the closure property, the commutative law, the associative law and the distributive law over addition.
One is the multiplicative identity for rational numbers.
Every nonzero rational number $\frac{p}{q}$ has its multiplicative inverse $\frac{q}{p}$.
Zero does not have its multiplicative inverse.

Order properties of rational numbers
Property 1: For each rational number x, one and only one of the following is true.
(i) x > 0    (ii) x = 0   (iii) x < 0
Property 2: For any two rational numbers x and y, one and only one of the following is true.
(i) x > y    (ii) x = y     (iii) x < y
Property 3: If x, y, z be any three rational numbers such that x > y and y > z ; then x > z.

The role of zero (0)
Look at the following.
2 + 0 = 0 + 2 = 2              (Addition of 0 to a whole number)
– 5 + 0 = … + … = – 5     (Addition of 0 to an integer)

$\frac{-2}{7}+0\dots =0+\left(\frac{-2}{7}\right)=\frac{-2}{7}$    (Addition of 0 to a rational number)

You have done such additions earlier also. Do a few more such additions.
What do you observe? You will find that when you add 0 to a whole number, the sum is again that whole number. This happens for integers and rational numbers also.
In general, a + 0 = 0 + a = a, where a is a whole number
b + 0 = 0 + b = b, where b is an integer
c + 0 = 0 + c = c, where c is a rational number
Zero is called the identity for the addition of rational numbers. It is the additive identity for
integers and whole numbers as well.

The role of 1
We have,  5 × 1 = 5 = 1 × 5 (Multiplication of 1 with a whole number)

$\begin{array}{l}\frac{-2}{7}\times 1=\dots \times \dots =\frac{-2}{7}\\ \frac{3}{8}\times \dots =1\times \frac{3}{8}=\frac{3}{8}\end{array}$

What do you find?
You will find that when you multiply any rational number with 1, you get back that rational number as the product. Check this for a few more rational numbers.

You will find that, a × 1 = 1 × a = a for any rational number a.
Negative of a number
While studying integers you have come across negatives of integers. What is the negative of 1? It is – 1 because 1 + (– 1) = (–1) + 1 = 0
So, what will be the negative of (–1)? It will be 1.
Also, 2 + (–2) = (–2) + 2 = 0, so we say 2 is the negative or additive inverse of –2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a.
For the rational number $\frac{2}{3}$ , we have $\frac{2}{3}+\left(-\frac{2}{3}\right)=\frac{2+(-2)}{3}=0$.

Also $\left(-\frac{2}{3}\right)+\frac{2}{3}=0$

Similarly $\frac{-8}{9}+\dots =\dots +\left(\frac{-8}{9}\right)=0$

$\dots +\left(\frac{-11}{7}\right)=\left(\frac{-11}{7}\right)+\dots =0$

In general, for a rational number $\frac{a}{b}$, we have $\frac{a}{b}+\left(-\frac{a}{b}\right)=\left(-\frac{a}{b}\right)+\frac{a}{b}=0$

We say that $\frac{–a}{b}$ is the additive inverse of $\frac{a}{b}$ and $\frac{a}{b}$ is the additive inverse of $\left(–\frac{a}{b}\right)$.

Reciprocal
By which rational number would you multiply $\frac{8}{21}$ , to get the product 1? Obviously by $\frac{21}{8}$ , since $\frac{8}{21}\times \frac{21}{8}=1$.

Similarly, $\frac{–5}{7}$must be multiplied by $\frac{7}{–5}$ so as to get the product 1.

We say that $\frac{21}{8}$is the reciprocal of $\frac{8}{21}\text{ and }\frac{7}{-5}$ is the reciprocal of $\frac{–5}{7}$.

Can you say what is the reciprocal of 0 (zero)?
Is there a rational number which when multiplied by 0 gives 1? Thus, zero has no reciprocal.
We say that a rational number $\frac{c}{d}$ is called the reciprocal or multiplicative inverse of another
rational number $\frac{a}{b}\text{ if }\frac{a}{b}\times \frac{c}{d}=1$.

Distributivity of multiplication over addition for rational numbers
To understand this, consider the rational numbers $\frac{-3}{4},\frac{2}{3}\text{ and }\frac{-5}{6}$ .

$\frac{-3}{4}\times \left\{\frac{2}{3}+\left(\frac{-5}{6}\right)\right\}=\frac{-3}{4}\times \left\{\frac{\left(4\right)+(-5)}{6}\right\}=\frac{-3}{4}\times \left(\frac{-1}{6}\right)=\frac{3}{24}=\frac{1}{8}$

Also $\frac{-3}{4}\times \frac{2}{3}=\frac{-3\times 2}{4\times 3}=\frac{-6}{12}=\frac{-1}{2}$

And $\frac{-3}{4}\times \frac{-5}{6}=\frac{5}{8}$

Therefore $\left(\frac{-3}{4}\times \frac{2}{3}\right)+\left(\frac{-3}{4}\times \frac{-5}{6}\right)=\frac{-1}{2}+\frac{5}{8}=\frac{1}{8}$

Thus, $\frac{-3}{4}\times \left\{\frac{2}{3}+\frac{-5}{6}\right\}=\left(\frac{-3}{4}\times \frac{2}{3}\right)+\left(\frac{-3}{4}\times \frac{-5}{6}\right)$ .