- CONSTRUCTION OF TRIANGLES
Any one of the following sets of measurements are required to construct a triangle
• Length of the three sides
• Two sides and the included angle
• Two angles and the included side
• Length of the hypotenuse and one side in case of a right-angled triangle.
Construction of a triangle when measurements of its three sides are given
Construct ΔABC, when AB = 6 cm, BC = 7 cm and CA = 9 cm. 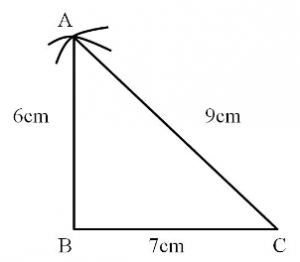
Steps of construction:
Step 1: Draw line segment BC = 7 cm.
Step 2: Draw an arc with B as the centre and the radius equal to 6 cm.
Step 3: Draw an arc with C as the centre and the radius equal to 9 cm.
Step 4: Name the point of intersection of these two arcs as A.
Step 5: Join points A and B, and points A and C.
Triangle ABC is the required triangle.
Construction of a triangle when measurements of two sides and the included angle are given
Construct ΔPQR, when PQ = 4 cm, QR = 6 cm and ∠PQR = 60°. 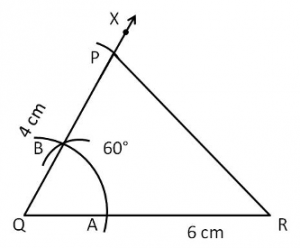
Steps of construction:
Step 1: Draw line segment QR = 6 cm.
Step 2: Construct an angle of 60° at point Q.
Step 3: Draw an arc on the ray QX with Q as the centre and the radius equal to 4 cm.
Step 4: Name the point where the arc cuts ray QX, as P.
Step 5: Join points P and R.
Triangle PQR is the required triangle.
Construction of a triangle, when two angles and the included side are given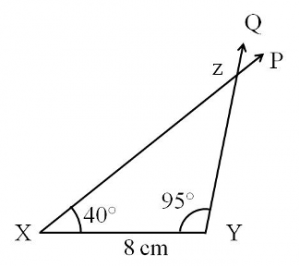
Construct ΔXYZ, when ∠ZXY = 40°, ∠XYZ = 95° and the included side XY = 8 cm.
Steps of construction:
Step 1: Draw line segment XY = 8 cm.
Step 2: Construct an angle of 40° at X with XY.
Step 3: Construct another angle of 95° at Y with YX.
Step 4: Name the point of intersection of the two rays as Z.
Triangle XYZ is the required triangle.
Construction of a right-angled triangle, when the length of one side and the hypotenuse are given
Construct a right-angled triangle LMN, with hypotenuse LN = 8 cm and side MN = 5 cm.
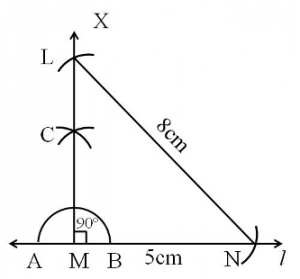
Steps of construction:
Step 1: Draw line ‘l‘.
Step 2: Mark a point on ‘l‘ and name it M.
Step 3: Draw a line segment MN = 5 cm on ‘l‘ .
Step 4: Construct a right angle XMN at M.
Step 5: Draw an arc with N as the centre and radius equal to 8 cm, such that it intersects MX.
Step 6: Mark the point of intersection as L.
Step 7: Join points L and N.
Triangle LMN is the required triangle.
- A triangle PQR has the measurements PQ = 6 cm, QR = 4.5 cm and RP = 5 cm. Which among the following is the first step of construction?
(A) With P as the centre and radius 5 cm, draw an arc.
(B) Draw a line segment PQ of length 6 cm.
(C) With Q as the centre and radius 4.5 cm, draw another arc to cut the previous arc at R.
(D) Join P to R and join Q to R.
- The measurements of a triangle ABC are AB = 4.5 cm, BC = 6.1 cm and CA = 5.6 cm. Which of the following is the last step in the construction of triangle ABC?
(A) Join A and B, A and C.
(B) Draw a line segment BC of length 6.1 cm.
(C) With B as the centre and radius 4.5 cm, draw an arc.
(D) With C as the centre and radius 5.6 cm, draw an arc to cut the previous arc at A.
- The following are the steps for construction of a triangle XYZ, with measures YZ = 8 cm, ∠Z = 55° and XY = 5.5 cm.
(i) Draw a line segment YZ of length 8 cm.
(ii) With Y as centre and radius 5.5 cm draw an arc to cut the ray ZP at X.
(iii) Join X to Y.
(iv) From Z draw a ray ZP making an angle of 55° with ZY.
The proper order of steps for construction is ____.
(A) i, ii, iii, iv (B) i, iv, ii, iii (C) i, iv, iii, ii (D) iv, i, iii, ii
- A unique triangle can be constructed with the measurements BC = 5 cm, AB = 4 cm and ∠B = 40°.
(A) True
(B) False
- The following are the steps for construction of a triangle ABC, with BC = 4.2 cm, ∠B = 45°,
∠A = 70°:
(i) Ray BX intersects CY at A.
(ii) Draw a line segment BC of length 4.2 cm
(iii) From B, draw a ray BX making an angle of 45° with BC
(iv) From C, draw a ray CY making an angle of 65° with CB.
The proper order of steps for construction is ____.
(A) iv, iii, ii, I (B) i, ii, iii, iv (C) i, iii, iv, ii (D) ii, iii, iv, i
- Which of the following figures would look like the given rough sketch of the triangle ABC with measures AB = 5cm, ∠A = 70° and ∠B = 70°?
| (A) | 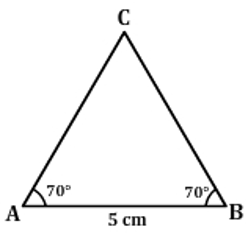 |
(B) | 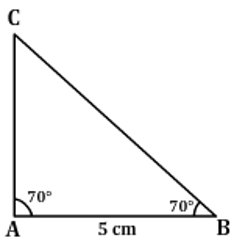 |
| (C) | 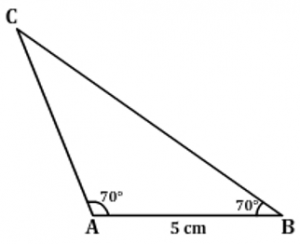 |
(D) | 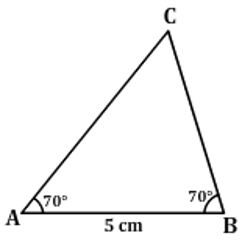 |
- The following are the steps for construction of a right angled triangle DEF, right angled at E with hypotenuse 6 cm long and one of its legs 4 cm long:
(i) Draw a line segment EF of length 4 cm.
(ii) From E, draw a ray EX perpendicular to EF.
(iii) Join F and D.
(iv) With F as the centre and radius 6 cm, draw an arc to cut EX at D.
The proper order of steps for construction is ____.
(A) i, ii, iii, iv (B) i, ii, iv, iii (C) iv, iii, ii, i (D) i, iv, iii, ii
- CONSTRUCTION OF PARALLEL LINES
Two lines in a plane that never meet each other at any point are said to be parallel to each other.
Any line intersecting a pair of parallel lines is called a transversal.
Properties of angles formed by parallel lines and transversal
• All pairs of alternate interior angles are equal.
• All pairs of corresponding angles are equal.
• All pairs of alternate exterior angles are equal.
• The interior angles formed on the same side of the transversal are supplementary (the sum of their measures is 180°).
Construction of a parallel line using the alternate interior angle property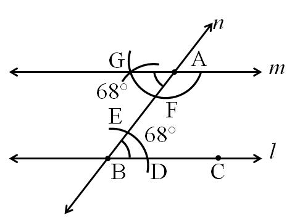
Step 1: Draw line ‘l’ and point A outside it.
Step 2: Mark point B on line ‘l’.
Step 3: Draw line ‘n’ joining point A and point B.
Step 4: Draw an arc with B as the centre, such that it intersects line ‘l’ at D and line ‘n’ at E.
Step 5: Draw another arc with the same radius and A as the centre, such that it intersects line ‘n’ at F. Ensure that arc drawn from A cuts the line ‘n’ between A and B.
Step 6: Draw another arc with F as the centre and distance DE as the radius.
Step 7: Mark the point of intersection of this arc and the previous arc as G.
Step 8: Draw line ‘m’ passing through points A and G.
Line ‘m’ is the required parallel line.
Verification of the construction
If the pair of alternate interior angles are equal in measure, then line ‘m’ is parallel to line ‘l‘. Construction of a parallel line using the corresponding angle property 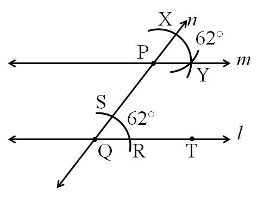
Step 1: Draw line ‘l’ and point P outside it.
Step 2: Mark point Q on line ‘l’.
Step 3: Draw line ‘n’ joining point P and point Q.
Step 4: Draw an arc with Q as the centre, such that it intersects line ‘l’ at R and line ‘n’ at S.
Step 5: Draw another arc with the same radius and P as the centre, such that it intersects line ‘n’ at X. Ensure that arc drawn from P cuts the line ‘n’ outside QP.
Step 6: Draw another arc with X as the centre and distance RS as the radius, such that it intersects the previous at Y.
Step 7: Draw line ‘m’ passing through points P and Y.
Line ‘m’ is the required parallel line.
Verification of the construction
If the pair of corresponding angles are equal in measure, then line ‘m’ is parallel to line ‘l‘.
- In order to construct a line parallel to a given line through a point not on it, which of the following properties are used?
(A) Properties regarding transversal and parallel lines
(B) Properties regarding intersecting lines
(C) Properties regarding sum of the angles of a triangle
(D) Properties regarding relationship between sides of a triangle
- The steps to be followed to construct a line parallel to a given line through a point not on it are as follows:
(i) Draw a line ‘l’ and mark a point P on it and a point R outside.
(ii) With P as centre and a convenient radius draw an arc to cut l at Q and PR at S.
(iii) Join P to R.
(iv) With R as centre and radius PQ drawn an arc AB to cut PR at C.
(v) Using compasses measure the arc length QS and with C as centre and the same arc length cut the arc AB at H.
(vi) Now join R to H to draw a line m.
The proper order of steps for construction is ____.
(A) iii, i, v, ii, iv, vi (B) v, i, ii, iii, vi, iv
(C) i, iii, ii, iv, v, vi (D) i, iv, vi, iii, ii, v
- In order to construct a line parallel to a given line through a point not on it, which of the following properties are used?
(A) Sum of the three angles of a triangle is 1800
(B) Alternate interior angles are equal
(C) Exterior angle of a triangle is equal to the sum of its two interior opposite angles
(D) Pythagoras property
- For the figure given below, steps to construct a line parallel to a given line through a point not on it are given, in step 3 the relation between the arcs SQ and CH is ____.
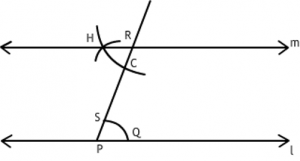
(A) arc SQ is greater than arc CH
(B) arc SQ is lesser than arc CH
(C) arc SQ is equal to arc CH
(D) there is no specific relation between the arc SQ and arc CH
- Following are the steps of construction for a line parallel to a given line at a distance of 3 cm from it.
(i) Draw a ray AY which is perpendicular to .
(ii) Draw a line CA.
(iii) Locate a point X on such that AX = 3 cm.
(iv) ∠BXY = 90° and ∠CAX = 90°. But ∠BXY and ∠CAX are corresponding angles.
(v) Draw a line BD which is perpendicular to passing through X.
The proper order of steps for construction is ____.
(A) i, ii, iii, iv, v (B) ii, i, iii, v, iv (C) iii, i , ii, v, iv (D) v, ii, i , iii, iv
NCERT TEXT BOOK EXERCISES
EXERCISE-10.1
- Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
- Draw a line l. Draw a perpendicular to lat any point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
- Let lbe a line and P be a point not on l. Through P, draw a line m parallel to l. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
EXERCISE-10.2
- Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
- Construct an equilateral triangle of side 5.5 cm.
- Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this?
- Construct ΔABC such that AB = 2.5 cm, BC = 6 cm and AC = 6.5 cm. Measure ∠B.
EXERCISE-10.3
- Construct ΔDEF such that DE = 5 cm, DF = 3 cm and m∠EDF = 90°.
- Construct ΔABC with BC = 7.5 cm, AC = 5 cm and m∠C = 60°.
EXERCISE-10.4
- Construct ΔABC, given m∠A = 60°, m∠B = 30° and AB = 5.8 cm.
- Construct ΔPQR if PQ = 5 cm, m∠PQR = 105° and m∠QRP = 40°.
(Hint: Recall angle sum property of a triangle).
- Examine whether you can construct ΔDEF such that EF = 7.2 cm, m∠E =
110° and m∠F = 80°. Justify your answer.
EXERCISE-10.5
- Construct the right angled ΔPQR, where m∠Q = 90°, QR = 8 cm and PR = 10 cm.
- Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long.
- Construct an isosceles right-angled triangle ABC, where, m∠ACB = 90° and AC = 6 cm.








