Lines and Angles

1. ANGLE
The inclination between two rays having a common initial point is called an angle. The two rays forming an angle are called the arms (or) sides of the angle. The common end point of the two rays forming an angle is called the vertex of the angle.
An angle is denoted by the symbol ‘ $\angle$ ’

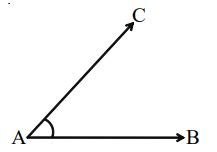
In the above figure, the rays AB and AC form an $\angle$BAC or $\angle$CAB having ‘A’ as vertex and AB,AC as its arms. We may also denote this angle by $\angle$A . When there are more than one angles in a figure, we label them 1,2,3 etc. and call them $\angle 1,\angle 2,\angle 3$ etc.

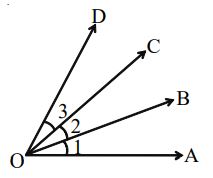
Thus, in the above figure $\mathrm{\angle }\mathrm{BOA}=\mathrm{\angle }1,\mathrm{\angle }\mathrm{COB}=\mathrm{\angle }2\text{ and }\mathrm{\angle }\mathrm{COD}=\mathrm{\angle }3$

Measuring Angles
The magnitude of an angle is the amount of rotation through which one of the arms must be rotated about the vertex to bring it to the position of the other. A complete turn about a point is divided into 360 equal parts, each called a degree. Written as 1°. The standard unit of measuring an angle is degree, to be denoted by ‘0’. One degree is further divided into 60 equal parts, each called one minute, written as 1′ . Thus $1^0=60‘$ . One minute in further divided into 60 equal parts are called one second, written as 1″ Thus $1^0=60“$

2. TYPES OF ANGLES
Acute Angle
An angle whose measure is more than $0^0$ but less than ${90}^0$ is called an acute angle. In the adjoining

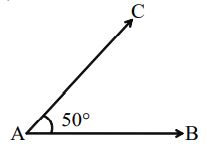
In the above figure, $\mathrm{\angle }\mathrm{ABC}={50}^{\circ }<{90}^{\circ }$

Therefore $\angle$ABC is an acute angle

Right Angle
An angle whose measure is ${90}^0$ is called a right angle.

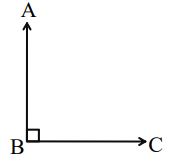
In the above figure, $\angle ABC={90}^0$

Therefore $\angle$ABC is an right angle
Obtuse Angle
An angle whose measure is more than ${90}^0$ but less than ${180}^0$ is called an obtuse angle

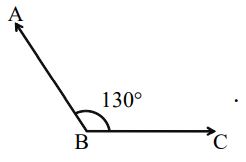
In the above figure, $\angle ABC={130}^0$
Clearly 90° < 130° < 180°
Therefore $\angle$ABC is an obtuse angle

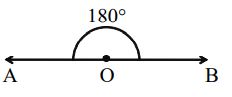
Straight Line
An angle whose measure is 180° is called a straight line

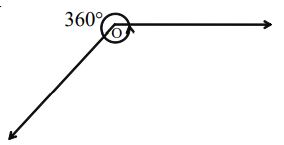
Reflex Angle
An angle whose measure is more than ${180}^0$ but less than ${360}^0$ is called a reflex angle.

Complementary Angles
Two angles are said to be complementary, if the sum of their measures is ${90}^0$. Each one of these angles is called the complement of the other.
Eg:

• Complement of ${40}^0=\left({90}^0-{40}^0\right)={50}^0$
• Complement of ${50}^0=\left({90}^0-{55}^0\right)={35}^0$
Supplementary Angles
Two angles are said to be supplementary, if the sum of their measures is ${180}^0$
. These angles is called the supplement of the other.
Eg:

• Supplement of ${80}^0=\left({180}^9-{80}^{\circ }\right)={100}^{\circ }$
 • Supplement of ${45}^0=\left({180}^0-{45}^0\right)={135}^{\circ }$
Adjacent Angles
Two angles having a common vertex and a common arm such that the other arms of the angles are on the opposite sides of the common arm, are known as adjacent angles.

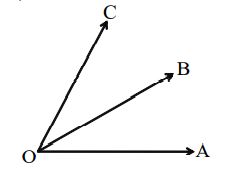
In the given figure, $\angle$AOB and $\angle$BOC are adjacent angles, since they have a common vertex ‘O’. A common arm of OB and their other arms OA and OC are on the opposite sides of the common arm OB.
Linear Pair of Angles
A pair of adjacent angles is said to be a linear pair, if these angles have one arm common and other arms as opposite rays.

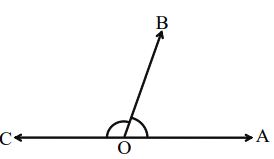
In the above figure, $\angle$AOB and $\angle$BOC form a linear pair of angles as they have a common arm OB and their other arms OA and OC are opposite rays.
Therefore $\angle$COA is a straight angle.
So $\mathrm{\angle }\mathrm{COA}={180}^{\circ }$

Therefore $\mathrm{\angle }\mathrm{AOB}+\mathrm{\angle }\mathrm{BOC}={180}^{\circ }$
Therefore the sum of a linear pair of angles is ${180}^0$
The sum of the angles at a point on a line on one side of the line is ${180}^0$

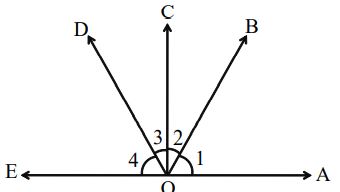
Thus, in the above figure, we have $\mathrm{\angle }1+\mathrm{\angle }2+\mathrm{\angle }3+\mathrm{\angle }4={180}^{\circ }$

Angles at a Point
The sum of all the angles at a point is ${360}^0$

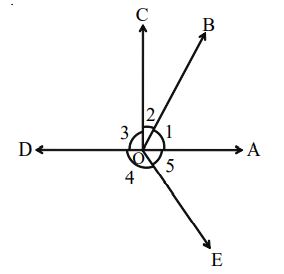
In the above figure, we have $\mathrm{\angle }1+\mathrm{\angle }2+\mathrm{\angle }3+\mathrm{\angle }4+\mathrm{\angle }5={360}^{\circ }$

Vertically Opposite Angles
When two lines intersect, then two angles having no common arm are called vertically opposite angles

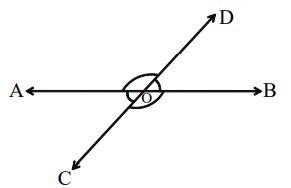
Let AB and CD be two lines intersecting at a point ‘O’.
Then $\angle$AOC and $\angle$BOD form one pair of vertically opposite angles.
$\angle$AOD and $\angle$BOC form another pair of vertically opposite angles.

When two lines intersect, then vertically opposite angles are always equal.
$\angle$AOC = $\angle$BOD and $\angle$AOD = $\angle$BOC .

3. PARALLEL LINES
If two lines are drawn in a plane such that they do not intersect, even when extended indefinitely in both the directions, then such line are called parallel lines. If lines ‘l’ and ‘m’ are parallel, we shown them by marking arrows on the lines pointing in the same directions and we write, $\frac{l}{m}$ read as ‘l’ is parallel to ‘m’

Transversal
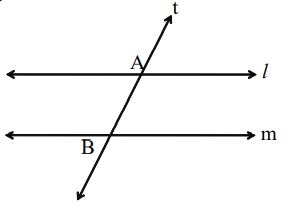
A line which intersects two distinct lines in a plane in exactly two points, is called a transversal. In the above figure, a line ‘t’ cuts two lines ‘l’ and ‘m’ at exactly two points A and B. So, ‘t’ is a transversal.

4. ANGLES FORMED WHEN A TRANSVERSAL CUTS TWO LINES
Suppose a transversal cuts two lines ‘l’ and ‘m’. Then the following angled are formed.

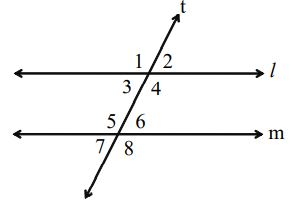
Two pairs of Interior alternate angles: $(\mathrm{\angle }3,\mathrm{\angle }6)\text{ and }(\mathrm{\angle }4,\mathrm{\angle }5)$   form two pairs of interior alternate angles.
Two pairs of Exterior alternate Angles: $(\mathrm{\angle }1,\mathrm{\angle }8)\text{ and }(\mathrm{\angle }2,\mathrm{\angle }7)$   form two pairs of exterior alternate angles.
Four pairs of corresponding Angles: $(\mathrm{\angle }1,\mathrm{\angle }5)(\mathrm{\angle }2,\mathrm{\angle }6)(\mathrm{\angle }3,\mathrm{\angle }7)\text{ and }(\mathrm{\angle }7,\mathrm{\angle }8)$   form four pairs of corresponding angles.
Two pairs of Co-interior or Co-joined or Allied angles : $(\mathrm{\angle }3,\mathrm{\angle }5)\text{ and }(\mathrm{\angle }4,\mathrm{\angle }6)$  form two pairs of Co-interior angles.
Results when two Parallel lines are cut buy a Transversal
Let AB and CD be two parallel lines, cut by a transversal ‘t’. Then,

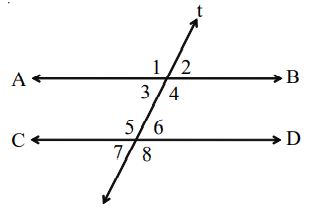
1. Interior alternate angles are equal $\mathrm{\angle }3=\mathrm{\angle }6\text{ and }\mathrm{\angle }4=\mathrm{\angle }5$
2. Exterior alternate angles are equal $\mathrm{\angle }1=\mathrm{\angle }8\text{ and }\mathrm{\angle }2=\mathrm{\angle }7$
3. Corresponding angles are equal $\mathrm{\angle }1=\mathrm{\angle }5,\mathrm{\angle }2=\mathrm{\angle }6,\mathrm{\angle }3=\mathrm{\angle }7\text{ and }\mathrm{\angle }4=\mathrm{\angle }8$
4. Co-interior angles are supplementary $\mathrm{\angle }3+\mathrm{\angle }5={180}^{\circ }\text{ and }\mathrm{\angle }4+\mathrm{\angle }6={180}^{\circ }$

5. CONDITION OF PARALLELISM OF TWO LINES
If two straight lines are cut by a transversal such that,
• A pair of alternate angles are equal.
• A pair of corresponding angles are equal
• The sum of the interior angles on the same side of the transversal is two right angles, then the two straight lines are parallel to each other.