1. RECALL
Natural Numbers
The numbers 1, 2, 3…… are used for counting objects is called ‘Natural Numbers’. Set of natural
numbers are represented by ‘N’.
Set of natural numbers N = { 1, 2, 3 …… }
Whole Numbers
Including ‘0’ in the collection of natural numbers is called whole numbers.
Set of whole numbers are represented by ‘W’.
Set of whole numbers W = {0, 1, 2, 3 ……}
Numbers greater than 0 are called positive numbers. Extending the number line to the left of 0 allow us to picture negative numbers, numbers that are less than 0.

When a single + sign or no sign is in front of a number, the number is a positive number. When a single – sign is in front of a number, the number is a negative number.
– 5 indicates “negative five”.
5 and + 5 indicate “positive five”.
The number 0 is neither positive nor negative.
Reading and writing integers
• The sign of an integer is read first before the number.
Example : – 5 is read as ‘negative five’.
+ 9 is read as ‘positive 9’ or simply ‘nine’.
• 0 is an integer but it is nothing positive nor negative.
Representing Integers on Number Lines
Integers can be represented on a number line.
The number line shows that every integer has an opposite number except ‘0’.
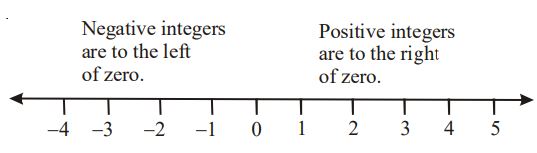
Comparing the Values of Two Integers
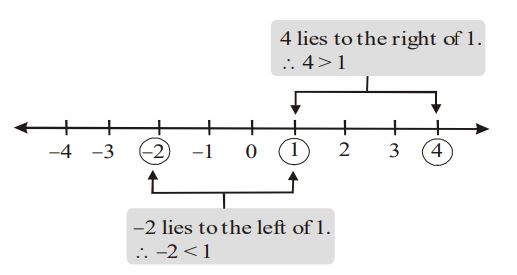
Number line can be used to compare the values of two integers.
1. Horizontal number line
(A) On a horizontal number line, an integer is greater than the integer on its left.
(B) On a horizontal number line, an integer is less than the integer on its right.
2. Vertical number line
(A) On a vertical number line, an integer is greater than the integer below it.
(B) On a vertical number line, an integer is less than the integer above it.
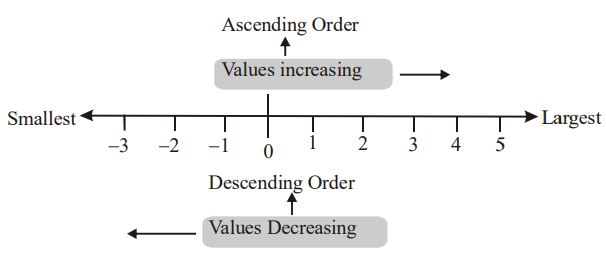
Arranging Integers in Order
1. Number lines can be used to arrange order, integers in increasing or decreasing order.
2. The value of integers on a horizontal number line increases from left to right and decreases from right to left.
Writing Positive and Negative Integers to Represent Word Descriptions
A positive or negative number is used to denote:
(A) An increase or a decrease in value
Example:
(i) Rs. 70 withdrawn is denoted by –Rs. 70.
(ii) Rs.70 deposited is denoted by + Rs.70.
(B) Values more than zero values less than zero
Example :
(i) – denotes a temperature that is below .
(ii) + denotes a temperature that is above .
(C) A positive direction or a negative direction (opposite direction)
Example:
(i) – denotes an anticlockwise rotation of .
(ii) + denotes a clockwise rotation of .
(iii) +5 m denotes a direction 5 m to the right.
(iv) –5 m denotes a direction 5 m to the left.
(D) Position above or below sea level
(i) The sea level is taken as 0 m.
(ii) Anything above sea level is taken as positive. For example if a bird is flying at 50m above, then we say +50m.
(iii) Similarly if a submarine lies 150 m below sea level we write it as –150m.
Comparison of Integers: If we represent two integers on the number line, then the integer
occurring on the right is greater than that occurring on the left.
Note:
• 0 is less than every positive integer
• Every negative integer is less than every positive integer.
• The greater is the integer, the lesser is its negative.
2. PROPERTIES OF INTEGERS ON ADDITION AND SUBTRACTION
(A) If a and b are two integers then a + b = c; where c is also an integer.
(B) For any two integers a and b
a + b = b + a
Which means that if we change the order of the integers, even then their sum does not change.
(C) For any three integers a, b and c
(a + b) + c = a + (b + c)
This means that even if we rearrange the integers their sum does not change.
(D) If a is any integer then a + 0 = a
This means that the sum of any integer and zero is the integer itself.
Example: – 10 + 0 = – 10
6 + 0 = 6
– 15 + 0 = – 15
(e) For every integer a (which is not zero) there is another integer – a such that
a + (– a) = 0
Example: 3 + (– 3) = 0
5 + (– 5) = 0
6 + (– 6) = 0
(f) The difference of any two integers is an integer i.e.
If a and b are two integers then a – b = c, where c is also an integer.
(g) In the whole numbers, 0 has no predecessor. But in integers – 1 is the predecessor of 0, –2 is the predecessor – 1 and so on.
Thus if a is any integer, then a – 1 is its predecessor.
(h) If a is any integer then a – 0 = a
Like signs Unlike signs
+ (+y) = +y + (– y) = – y
– (–y) = + y – (+ y) = – y
3. MULTIPLICATION OF INTEGERS
1. The multiplication of an integer with a positive integer is the repeated addition of the integer.
2. Rules for multiplication of integers:

(A) The product of two integers is positive when both integers have like signs [as in (i) and (iv)].
(B) The product of two integers is negative when both integers have unlike signs [as in (ii) and (iii)].
(C) The product of an integer and zero is always zero [as in (v) and (vi)].
Property 1: If a and b are integers than a × b is also an integer
Property 2: If a and b are two integers then a × b = b × a
Property 3: If a, b and c are any three integers then a × (b × c) = (a × b) × c
Property 4: The product of an integer and zero (0) is always zero (0), i.e., for any integer a, a × 0 = 0 × a = 0.
Property 5 : The product of an integer and 1 is the integer itself.
i.e., for any integer a, a × 1 = 1 × a = a.
Property 6: For any integers a, b and c,
a × ( b + c) = (a × b) + (a × c)
a × ( b – c) = (a × b) – (a × c)
(A) When the number of negative integers in a product is ODD, the product is negative.
(B) When the number of negative integers in a product is EVEN, the product is positive.








