Fractions and Decimals

1. FRACTIONS RECALL
Fractions: The number of the form $\frac{a}{b}$; where ‘a’ and ‘b’ are whole numbers and $b\ne 0$.
Example: $\frac{2}{5}$ is a fraction in which numerator is 2 and denominator is 5.
Types of Fractions
Simple Fraction
A fraction of the form $\frac{a}{b}$ , where ‘a’ and ‘b’ are whole numbers and $b\ne 0$.
Example: $\frac{3}{5},\frac{11}{13},\frac{7}{11},\frac{24}{31}\text{ etc. }$
Complex Fraction
A fraction of the form $\frac{x}{y}$ where ‘x’ and ‘y’ are fractions.
we define $\frac{\left(\frac{a}{b}\right)}{\left(\frac{a}{d}\right)}=\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}\times \frac{d}{c}$
2. CLASSIFICATION OF FRACTIONS
• Decimal Fraction: Is a fraction whose denominator is 10, 100, 1000 etc.,
Example: $\frac{3}{10},\frac{7}{100},\frac{11}{1000},\frac{13}{10000}\text{ etc. }$
• Vulgar Fraction: Is a fraction whose denominator is a whole number other than 10, 100, 1000 etc.,
Example: $\frac{2}{5},\frac{5}{3},\frac{3}{7},\text{ etc. }$
• Proper Fraction: Is a fraction where the numerator of a fraction is less than its denominator.
Example: $\frac{2}{5},\frac{4}{7},\frac{11}{21},\text{ etc. }$

• Improper Fraction: Is a fraction where the numerator of a fraction is greater than or equal to its denominator.

Example : $\frac{14}{11},\frac{13}{9},\frac{7}{5},\text{ etc. }$

• Mixed Number: A number which can be expressed as the sum of a natural number and a proper fraction is called a mixed number.

Example : $1\frac{2}{3},3\frac{5}{7},7\frac{4}{11},\text{ etc. }$

Conversion of mixed number to an Improper Fraction
Multiply the denominator of the proper fraction with integral part and add numerator of the proper fraction to it. This gives the numerator of the improper fraction and its denominator is the same as that of proper fraction.
Example: $8\frac{11}{13};8\frac{11}{13}-\frac{8\times 13+11}{13}-\frac{104+11}{13}=\frac{115}{13}$

Conversion of Improper Fraction to a Mixed Number
Divide the numerator of the given fraction by its denominator. The quotient so obtained forms the whole number part and the remainder forms the numerator of the fractional part of the mixed number.
Example: $\frac{14}{3}$

On dividing 14 by 3, quotient = 4 ; remainder = 2

$\therefore \frac{4}{13}=4\frac{2}{3}$

Equivalent Fractions
A given fraction and the fraction obtained by multiplying (or dividing) both of its numerator and
denominator by the same non-zero number are called equivalent fractions.

Example: $\frac{2}{3}=\frac{2\times 2}{3\times 2}=\frac{2\times 3}{3\times 3}\text{ etc }$

$\therefore \frac{2}{3},\frac{4}{6},\frac{6}{9},\frac{8}{12}$ etc are equivalent fractions
$\frac{16}{24}-\frac{16÷8}{24÷8}-\frac{2}{3}$ etc are equivalent fractions

Like Fractions: are fractions having the same denominators but different numerators.

Example: $\frac{3}{5},\frac{4}{5},\frac{6}{5},\frac{11}{5}$are like fractions

Unlike Fractions: are the fractions having different denominators.

Example: $\frac{2}{3},\frac{3}{5},\frac{7}{11},\frac{13}{17}$ are unlike fractions.

Conversion of Unlike to Like Fractions
Step1: Find the L.C.M of the denominators of all the given fractions.
Step2: Change each given fraction into an equivalent fraction having denominator as the L.C.M of denominators of the given fractions.
Example: Convert $\frac{3}{5},\frac{5}{7}$  in to like fractions
Take L.C.M of denominators L.C.M of 5, 7 is 35.

Clearly

$\begin{array}{l}\frac{3\times 7}{5\times 7}=\frac{21}{35}\\ \frac{5\times 5}{7\times 5}=\frac{25}{35}\end{array}$

Now $\frac{21}{35},\frac{25}{35}$ are like fractions

Comparison of Fractions
There are two methods to compare fractions.
Method 1: Cross Product Method:

Two fractions $\frac{a}{b}\text{ and }\frac{c}{d}$ may be compared as under cross multiply as show $\frac{a}{b}\times \frac{c}{d}$, then

$\begin{array}{r}\text{· If }\mathrm{a}\times \mathrm{d}>\mathrm{b}\times \mathrm{c},\text{ then }\frac{\mathrm{a}}{\mathrm{b}}>\frac{\mathrm{c}}{\mathrm{d}}\\ \text{· If }\mathrm{a}\times \mathrm{d}<\mathrm{b}\times \mathrm{c}, \text{ then }\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{c}}{\mathrm{d}}\\ \text{· If }\mathrm{a}\times \mathrm{d}=\mathrm{b}\times \mathrm{c}, \text{ then }\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}\end{array}$

Example: compare $\frac{5}{6},\frac{7}{8}$

Cross multiply as shown $\frac{5}{6}\times \frac{7}{8}$

We have 5 × 8 = 40 and 6 × 7 = 42

$42>40\therefore \frac{7}{8}>\frac{5}{6}$

Method2: Convert given fractions in to like fractions and then compare numerators.
Example: Compare $\frac{5}{6},\frac{7}{8}$

L.C.M of 6,8 is 48

$\begin{array}{l}\frac{5\times 8}{6\times 8}=\frac{40}{48}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\\ \frac{7\times 6}{8\times 6}=\frac{42}{48}\\ 42>40\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\\ \therefore \frac{7}{8}>\frac{5}{6}\end{array}$

3. MULTIPLICATIONS OF FRACTIONS
You know how to find the area of a rectangle. It is equal to length × breadth. If the length and breadth of a rectangle are 7 cm and 4 cm respectively, then what will be its area? Its area would be $7\times 4=28 c{m}^2$.

What will be the area of the rectangle if its length and breadth are $7\frac{1}{2}\mathrm{cm}\text{ and }3\frac{1}{2}\mathrm{cm}$ respectively? You will say it will be $7\frac{1}{2}\times 3\frac{1}{2}=\frac{15}{2}\times \frac{7}{2}{\mathrm{cm}}^2$. The numbers $\frac{15}{2} and \frac{7}{2}$ are fractions.
To calculate the area of the given rectangle, we need to know how to multiply fractions. We shall learn that now.
Multiplication of a Fraction by a Whole Number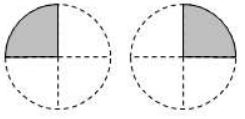

Observe the pictures at the left. Each shaded part is $\frac{1}{4}$ part of a circle. How much will the two shaded parts represent together?

They will represent $\frac{1}{4}+\frac{1}{4}=2\times \frac{1}{4}$

To multiply a mixed fraction to a whole number, first convert the mixed fraction to an improper fraction and then multiply.
Therefore, $3\times 2\frac{5}{7}=3\times \frac{19}{7}=\frac{57}{7}=8\frac{1}{7}$

4. MULTIPLICATION OF A FRACTION BY A FRACTION
Farida had a 9 cm long strip of ribbon. She cut this strip into four equal parts. How did she do it? She folded the strip twice. What fraction of the total length will each part represent?
Each part will be $\frac{9}{4}$ of the strip. She took one part and divided it in two equal parts by folding the part once. What will one of the pieces represent? It will represent $\frac{1}{2}\text{ of }\frac{9}{4}\text{ or }\frac{1}{2}\times \frac{9}{4}$

5. DIVISION OF FRACTIONS
John has a paper strip of length 6 cm. He cuts this strip in smaller strips of length 2 cm each. You know that he would get 6 $÷$ 2 = 3 strips.
John cuts another strip of length 6 cm into smaller strips of length $\frac{3}{2}cm$ each.
How many strips will he get now? He will get $6÷\frac{3}{2}$ strips

A paper strip of length $\frac{15}{2}cm$ can be cut into smaller strips of length $\frac{3}{2}cm$ each to give $\frac{15}{2}÷\frac{3}{2}$pieces.

So, we are required to divide a whole number by a fraction or a fraction by another fraction.
Let us see how to do that.
Reciprocal of a Fraction
The reciprocal of a non-zero fraction $\frac{a}{b}\text{ is }\frac{b}{a}$

Example: Reciprocal of $\frac{2}{5}\text{ is }\frac{5}{2}$

Division of Whole Number by a Fraction
Let us find $1÷\frac{1}{2}$

We divide a whole into a number of equal parts such that each part is half of the whole.
The number of such half $\left(\frac{1}{2}\right)$ parts would be Observe the figure. How many half parts do you see? There are two half parts.

$$\begin{gathered} So, 1÷\frac{1}{2}=2. \\ \text{Also }1\times \frac{2}{1}=1\times 2=2 \end{gathered}$$                          

$\text{ Thus, }1÷\frac{1}{2}=1\times \frac{2}{1}$

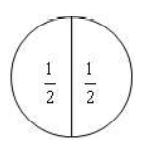
What will be $\frac{3}{4}÷3?$

Based on our earlier observations we have: $\frac{3}{4}÷3=\frac{3}{4}÷\frac{3}{1}=\frac{3}{4}\times \frac{1}{3}=\frac{3}{12}=\frac{1}{4}$

Division of a Fraction by Another Fraction
We can now find $\frac{1}{3}÷\frac{5}{6}$

$\frac{1}{3}÷\frac{5}{6}=\frac{1}{3}\times \text{ reciprocal of }\frac{5}{6}=\frac{1}{3}\times \frac{6}{5}=\frac{2}{5}$

A Fraction Lying between two given Fractions

If  $\frac{a}{b}\text{ and }\frac{c}{d}$ are two fractions, then the fraction $\frac{a+c}{b+d}$ lies between $\frac{\mathrm{a}}{\mathrm{b}}\text{ and }\frac{\mathrm{c}}{\mathrm{d}}$, thus $\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}$ .

6. DECIMALS RECALL
A fraction whose denominator is 10 or some integral power of 10, is called a decimal fraction.
Example: $\frac{2}{10},\frac{23}{100},\frac{234}{1000},\frac{2345}{10000}\text{ etc., }$

These decimal fractions can be written in the decimal form as 0.2, 0.23, 0.234, 0.2345 etc
Decimals: The number written in the decimal form are called decimal numbers or decimals.
Thus each of the numbers 0.2, 0.23, 0.234, 0.2345 is a decimal.
• A decimal has two parts. Whole number part and decimal part. These parts are separated by a dot (.) is called decimal point.
• The digits lying to the left of the decimal point form the whole number part.
• The decimal point together with digits lying to its right form the decimal part.
Eg: In the decimal number 23.574; Whole number part = 23 & Decimal part = 574
Decimal Places:
The number of digits contained in the decimal part of a decimal gives the number of its decimal places.
Example:

• 5.89 has 2 decimal places
• 23.758 has 3 decimal places
Like Decimals: Decimals having the same number of decimal places are called like decimals.
Example:

• 5.1, 77.3, 109.1, 1009.0 are like decimals; each having one decimal place
• 0. 85, 23.58, 134.72, 1000.89 are like decimals; each having two decimal places
Unlike Decimals: Some given decimals, all not having the same number of decimal places are called unlike decimals.
Example:

• 5.75, 57.5 are unlike decimals

7. COMPARISON OF DECIMALS
• If two decimals having greatest Integral part is greater.
Example:

45.85, 54.75
Since 54 > 45; hence 54.75 > 45.85
• If two decimals having same integral part, then compare the decimal number part which is having greatest decimal part is greater.
Example:

23.58, 23.78
58, 78 are in decimal part of these two
In this 78 > 58; hence 23.78 > 23.58
Conversion of Unlike to Like Decimals
Annexing zeroes to the extreme right of the decimal part of a decimal does not change its value.
Example:

$$\begin{gathered} 0.7=\frac{7}{10}=\frac{70}{100}=0.70 \\ 0.70=\frac{70}{100}=\frac{700}{1000}=0.7000 \\ 0.7=0.70=0.700\text{ etc. } \end{gathered}$$

Decimal to Fraction Conversion
Write the given decimal without the decimal point as numerator. Take ‘1’ annexed with as many zeroes as is the number of decimal places in the given decimal as denominator.

Example:

$\begin{array}{l}23.4=\frac{234}{10}\\ 23.45=\frac{2345}{100}\\ 23.456=\frac{23456}{1000}\end{array}$

Conversion of Fraction into a Decimal by Division Method:
Procedure:
Step1. Divide the numerator by the denominator
Step2. Complete the division. Let a non-zero remainder be left
Step3. Insert a decimal point in the dividend and the quotient.
Step4. Part a zero on the right of the decimal point in the dividend as well as on the right of the
remainder. Divide again just as whole numbers.
Step5. Repeat step4 still either the remainder is zero or requisite number of decimal places have been obtained.

8. TYPES OF DECIMALS
Terminating Decimals: In the process of converting a fraction into a decimal by the division method. If we obtain a zero remainder after a certain number of steps, then the decimal obtained is a terminating decimal.
Example: 3.175 is a terminating decimal.
However, there are situations where the division process continues indefinitely and zero remainder is never obtained. Such decimals are known as non-terminating decimals.
Example: $\frac{1}{19}=0.5263157\dots$

Repeating or Recurring Decimals: If in a decimal, a digit or a set of digits in the decimal part is repeated continuously, then such a number is called a recurring or repeating decimal. In a recurring decimal, if a single digit is repeated, then it is expressed by put a dot on it. If a set of digits is repeated, it is expressed by putting a bar on the set.

Example:

$\begin{array}{l}\frac{4}{9}-0.444\dots -0.\overline{4}\\ \frac{22}{7}=3.142857142857\dots \dots =3.\overline{142857}\end{array}$

Pure Recurring Decimal: Is a decimal in which all the digits in the decimal part are repeated.
Example: $0.\overline{2},0.\overline{59}\text{ etc. }$

Mixed Recurring Decimal: Is a decimal in which some of the digits in the decimal part are repeated and the rest are not repeated.
Example: $0.6\overline{3},0.5\overline{76},\text{ etc. }$

Zero of the Decimal: The value of a decimal number is not altered when zeros are replaced at the end of a number.

Example:
8 can be written as 8, 8.0, 8.00, 8.000………
The number 34.5 can be written as 34.50, 34.500,34.5000………

9. OPERATION ON DECIMALS
Addition of Decimals
• Convert all the given decimals into like decimals.
• Write the decimals one under the other with decimal points of all the addends in the same column.
• Add as in the case of whole numbers.
• In the sum, put decimal point directly under the decimal points of the addends.
Example: $\text{ Solve }5.7+8.78+0.352$

$5.700+8.780+0.352$

$$\begin{gathered} 5.700 \\ 8.780 \\ 0.352 \\ –––– \\ 14.832 \end{gathered}$$

Subtraction of Decimals
• Convert the given decimals into like decimals.
• Write the smaller number under the larger one in such a way that the decimal points of both the numbers are in the same column.
• Subtract as in the case of whole numbers.
• In the difference, put the decimal point directly under the decimal points of the given numbers.
Example: Solve 100.08 – 98.8

100.08 – 98.80
$$\begin{gathered} 100.08 \\ 97.80 \\ – \\ –––– \\ 1.28 \end{gathered}$$
Multiplication of Decimals: Multiplication of a decimal by 10,100,1000 etc., when a decimal is multiplied by some power of 10, then the decimal point is shifted to the right by as many digits as there are zeroes in the multiplier.
Example: 10.999 $\times$10 = 109.99
(shifted decimal point 1 place to the right)
10.999 $\times$ 100 = 1099.9
(shifted decimal point 2 places to the right)
Division of Decimals: To divide a decimal by 10,100,1000 etc., shift the decimal point to the left as many places as is the number of zeroes in the divisor.
Example: Divide $15.3÷10$

$15.3÷10=1.53$ (shifting decimal point one place to the left)
Dividing a Decimal by a Whole Number
Step1: Perform the division by considering the dividend a whole number
Step2: When the division of whole number part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Example: $2.345÷10$

$2.345÷10=0.2345$ (shifting decimal point one place to the left)

Dividing a Decimal by a Decimal
Step 1: Convert the divisor into a whole number by multiplying the dividend and divisor by a suitable power of 10.
Step 2: Divide the new dividend by the whole number obtained above
Example: Divide 55.50 by 5.55

$\frac{55.50\times 100}{5.55\times 100}=\frac{5550}{555}=10$