Congruence of Triangles

1. CONGRUENCY OF TRIANGLE
Congruent Figures
Geometrical figures which have exactly the same shape and the same size, are known as congruent figures. For congruence, we use the symbol ‘ $\cong$ ‘  read as ‘congruent to’. Thus, two plane figures are congruent if each when superposed on the other, covers it exactly.
Eg:

Similar Figures
Geometrical figures which have exactly the same shape but not necessarily the same size, are known as similar figures. For similarity, we use the symbol ‘ $\square$ ‘ read as ‘is similar to’
Note
Two congruent figures are always similar but two similar figures need not be congruent.
Eg:

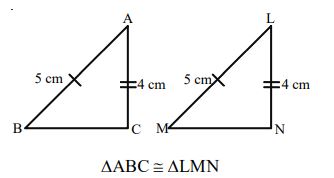
• Any two equilateral triangles are always similar, but they are congruent only if they have the same side length.
• Any two line segments are always similar, but they congruent only if they have the same length.
Congruent Triangles
Two triangles are said to be congruent, if each one of them can be made to superpose on the other, so as to cover it exactly. Thus, congruent triangles are exactly identical. In congruent triangles, the sides and angles which coincides by superposition are called corresponding sides and angles respectively. Hence, we can also say that two triangles are congruent if pairs of corresponding sides and corresponding angles are equal.

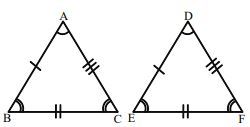
Thus $\mathrm{\Delta ABC}\cong \mathrm{\Delta DEF}\text{ if }\mathrm{AB}=\mathrm{DE},\mathrm{BC}=\mathrm{EF},\mathrm{CA}=\mathrm{FD}$

$\mathrm{\angle }\mathrm{A}=\mathrm{\angle }\mathrm{D},\mathrm{\angle }\mathrm{B}=\mathrm{\angle }\mathrm{E},\mathrm{\angle }\mathrm{C}=\mathrm{\angle }\mathrm{F}$

We write, $\mathrm{\Delta ABC}\cong \mathrm{\Delta DEF}$ , if means that A,B and C are matched with D,E and F respectively and we write $\mathrm{A}\leftrightarrow \mathrm{D},\mathrm{B}\leftrightarrow \mathrm{E}\text{ and }\mathrm{C}\leftrightarrow \mathrm{F}$ and therefore, $\mathrm{\Delta ABC}\leftrightarrow \mathrm{DEF}$

2. CONDITIONS FOR CONGRUENCY OF TRIANGLES
There are four cases as conditions for congruency. In each case, we have a different combination of the three matching parts.
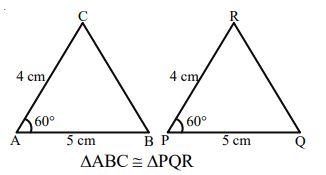
SAS (Side-Angle-Side)Condition
If two triangles have two sides and the included angle of the one respectively equal to two sides and the included angle of the other, then the triangles are congruent.
Eg:

ASA (Angle-Side-Angle)Condition
If two triangles have two angles and the included side of them one respectively equal to two angles and the included side of the other. Then the triangles are congruent.
Eg :

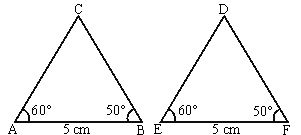
If two angles of one triangle are respectively equal to two angles of the other, then it is quite clear that their remaining third angles are also equal. Thus even, if the given side is not the one included between the two given angles, then it shall be the one included between one of the given angles and the third angle.
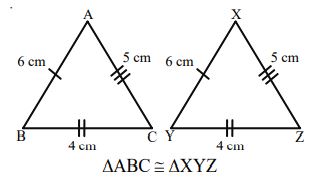
SSS (Side-Side-Side)Condition
If two triangles have the three sides of the one respectively equal to the corresponding three sides of the other, then the triangles are congruent.
Eg:

RHS (Right-Angle-Hypotenuse-Side)
If two right angled triangles have one-side and hypotenuse of the one respectively equal to the
corresponding side and the hypotenuse of the other, then the triangles are congruent.
Eg: