Fractions

1. UNDERSTANDING A FRACTION
A fraction is a number representing part of a whole. The whole may be a single object or a group of objects and each to be equal.
Definition

The numbers of the form $\frac{p}{q}$, where ‘p’ and ‘q’ are whole numbers and q $\ne$ 0 are called fractions.
Example:
$\frac{1}{2},\frac{2}{3},\frac{1}{4},\frac{3}{5},\frac{8}{12}$etc., are fractions, here $\frac{1}{2}$ means the whole thing can be divided into two equal parts and we taken out 1 part similarly $\frac{3}{3}$ means the whole thing can be divided into three equal parts and we take out two parts.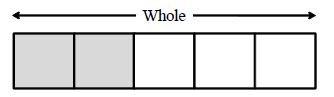

In the above figure the whole rectangle can be divided into 5 equal parts among which 2 parts are shaded. The shaded portion represents two-fifths and is denoted by $\frac{2}{5}$. Here two-fifths is a fractional number and $\frac{2}{5}$ is a fraction.
How to Read Fractions
$\frac{1}{2}$ read as one-half; $\frac{2}{3}$ as two-thirds; $\frac{1}{4}$ as one-quarter; $\frac{3}{5}$ as three-fifth and $\frac{8}{12}$ read as eight-twelths and so an.
Note:
For a given fractions $\frac{\mathrm{p}}{\mathrm{q}}$, p is called the numerator and q is called denominator. Where p, q may have common factors
Example:
$\frac{5}{12},\frac{1}{2},\frac{2}{3},\frac{6}{8},\frac{10}{12}$, etc, 5 is numerator and 8 is denominator
Fractions can also be written in its lowest terms.

Example:

(i) $\frac{5}{12},\frac{1}{2},\frac{2}{3}$  fractions does not have any common factors in both numerator and denominator.
They are written in lowest terms.
(ii) Fractions $\frac{6}{8},\frac{10}{12}$  have common factors in both numerator and denominator
We know that the numbers of the form $\frac{\mathrm{p}}{\mathrm{q}}$  where p,q $\in$ w (whole numbers), q $\ne$ 0 and p, q does not have any common factors are called rational numbers.
Example:
$\frac{1}{2},\frac{2}{3},\frac{4}{5},\frac{10}{11}$ , etc are rational numbers. Therefore ‘every rational number is a fraction’

2. SIMPLEST FORM OF A FRACTION
If the numerator and denominator of a fraction have no common factor except 1, then the fraction is said to be in its simplest form or in lowest terms. Or if a fraction is said to be in simplest form if the H.C.F of its numerator and denominator is 1.
I. Irreducible Fraction
If a fraction is in simplest form then it is called irreducible fraction.
II. Reducible Fraction
If a fraction is not irreducible fraction then it is called reducible fraction.
III. Method to find Simplest Form of a Fraction:
We can reduce given fraction into its simplest form using any of the following two methods.
Method 1
Divide numerator and denominator of given fraction by their H.C.F
Example:
To find simplest form of $\frac{9}{15}$; the H.C.F of 9 and 15 is 3. Now divide both numerator and denominator of $\frac{9}{15}$  by 3 to get reduce it into simplest form. Hence the simplest form of $\frac{9}{15}$ is $\frac{3}{5}$.
Method 2
In this method, we can divide both numerator and denominator of the given fraction by common factor till we are left with common 1 only.
Example:
We will find simplest form of $\frac{72}{90}$  using this method or follows, $\frac{72}{90}=\frac{4}{5}$. Therefore the simplest form of $\frac{72}{90}$  is $\frac{4}{5}$.

3. REPRESENTING FRACTIONS ON NUMBER LINE
To represent given fraction $\frac{1}{2}$ on a number line, we can divide the length between 0 and 1 into two equal parts and we can take 1 part as a fraction 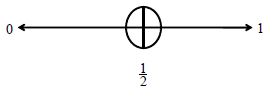$\frac{1}{2}$.

To represent $\frac{2}{3}$ on a number line, we can divide the length between 0 and 1 into three equal parts and we can take into three equal parts and we can take 2 parts out of 3 as a fraction 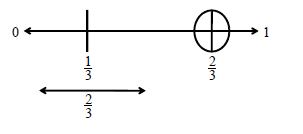$\frac{2}{3}$.

4. CLASSIFICATION OF FRACTIONS
I. Like Fractions
Fractions with the same denominator are called like fractions.
Example:
$\frac{1}{9},\frac{2}{9},\frac{4}{9},\frac{8}{9},\frac{16}{9}$ are like fractions.
II. Unlike Fractions
Fractions with different denominators are called unlike fractions.
Example:
$\frac{1}{2},\frac{2}{3},\frac{3}{5},\frac{5}{8}$ are unlike fractions.
III Unit Fractions
Fractions with 1 as numerator are known as unit fractions.
Example:
$\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{12}$, etc, are all unit fractions.
IV. Proper Fractions
A fraction in which the numerator is less than its denominator is called proper fraction.
Example:
$\frac{1}{2},\frac{2}{3},\frac{4}{5},\frac{8}{12}$, etc, are proper fractions lie between the 0 and 1 on a number line.
V. Improper Fractions
A fraction in which the numerator is greater than or equal to its denominator.
Note:
The numerical value of all the improper fraction does not lie between 0 and 1 on a number line.
VI. Mixed Fraction
A combination of a whole number and a proper fraction is called mixed fraction.
Example:
$2\frac{1}{3},3\frac{1}{4},16\frac{2}{3}$, etc, are all mixed fraction.
we can write mixed fraction = whole number part + fractional parts = whole number + $\frac{\text{ Numerator }}{\text{ Denominator }}$ of fractional part
In a mixed fraction $2\frac{1}{3}, 2$ is whole number and $\frac{1}{3}$ is a proper fraction. $2\frac{1}{3}=2+\frac{1}{3}$
VII. Equivalent Fraction
Two or more fractions representing the same point of a whole are called equivalent fractions.
Eg: $\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\frac{6}{12}–$…..are equivalent fractions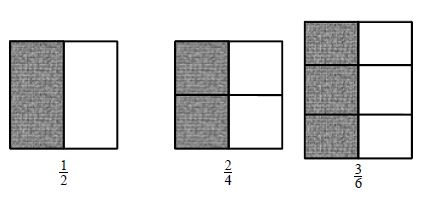

In above figures, the shaded regions of each figure are equal i.e., $\frac{1}{2}=\frac{2}{4}=\frac{3}{6}$ are equivalent fractions.
Finding Equivalent Fractions
To find an equivalent fraction of a given fraction, we can multiply or divide both numerator and denominator of the given fraction by the same non-zero number.
Examples:
$\frac{1}{2}=\frac{1\times 2}{2\times 2}=\frac{2}{4}; \frac{2\times 3}{4\times 3}=\frac{6}{12}$

$\frac{1}{2}=\frac{1\times 2}{2\times 2}=\frac{2\times 3}{4\times 3}=\frac{1\times 3}{2\times 3}=\frac{1\times 5}{2\times 5}=$…..      are equivalent fractions
$\frac{12}{18}=\frac{12÷2}{18÷2}=\frac{12÷3}{18÷3}=\frac{12÷6}{18÷6}$              are also equivalent fractions
Note:
If two fractions are said to be equivalent fractions, the product of the numerator of the first and denominator of the second is equal to the product of denominator of the first and the numerator of the second. These products are called cross products. If $\frac{\mathrm{p}}{\mathrm{q}},\frac{\mathrm{r}}{\mathrm{s}}$ are two fractions then their cross product is denoted as

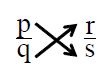
and if ps = rq then we say that $\frac{\mathrm{p}}{\mathrm{q}},\frac{\mathrm{r}}{\mathrm{s}}$ are equivalent fractions.
Example: $\frac{1}{2},\frac{2}{4}$ are equivalent fractions since 1 × 4 = 2 × 2 $\Rightarrow$4 = 4

5. INTER-CONVERSION OF FRACTIONS
I. Conversion of Unlike Fractions into Like Fractions
To convert unlike fractions we can make denominators of all given fractions equal to their L.C.M (i.e., we convert each of the given fractions into an equivalent fractions having a denominator equal to the L.C.M of all the denominators of the given fraction.)
Example:
To convert the unlike fractions $\frac{3}{4},\frac{5}{6},\frac{4}{9},\frac{1}{8},\frac{7}{12}$ into like fractions first we find L.C.M of denominator of given unlike fractions.
L.C.M of 4, 6, 9, 8, 12 = L.C.M of 8, 9,12 = 72
Now we are equating denominator of all fractions to 72 by multiplying numerators and denominators of all given fractions with a suitable number.

Therefore $\frac{3}{4}–\frac{3\times 18}{4\times 18}–\frac{54}{72}; \frac{5}{6}–\frac{5\times 12}{6\times 12}–\frac{60}{72}; \frac{4}{9}–\frac{4\times 8}{9\times 8}–\frac{32}{72}$; $\frac{1}{8}–\frac{1\times 9}{8\times 9}–\frac{9}{72}$ and $\frac{7}{12}=\frac{7\times 6}{12\times 6}–\frac{42}{72}$

Therefore $\frac{54}{72},\frac{60}{72},\frac{32}{72},\frac{9}{72},\frac{42}{72}$ are the required like fractions.

I Conversion of mixed Fraction into Improper Fraction
We know that mixed fraction has two parts; one is whole number part and the other is fractional part. To convert mixed fraction into improper fraction, multiply the whole number part with the denominator of the fractional part and add the product to the numerator of the fraction part. This gives the numerator of the improper fraction and its denominator is same as denominator of fraction part.
i.e., if mixed fraction = whole number $\frac{\text{ Numerator }}{\text{ Denominator }}$, then the improper fraction can be expressed as
Improper Fraction =$\frac{\text{ (Whole number }\times \text{ Denominator ) Numerator }}{\text{ Denominator }}$
Example:
Convert mixed fraction $5\frac{2}{3}$ into improper fraction as follows:
$5\frac{2}{3}=5–\frac{2}{3}\frac{(5\times 3)–2}{3}=\frac{15+2}{3}=\frac{17}{3}$

III. Convert an Improper Fraction into a Mixed Fraction
We know that improper fraction has greater numerical value of numerator than denominator. To convert an improper fraction into a mixed fraction, divide the numerator by denominator then the quotient so obtained forms the whole number part and the remainder forms numerator of  fractional part.
Here denominator of fractional part is same as denominator of given improper fraction. So that mixed fraction can be written as follows

Mixed Fraction Quotient$\frac{\text{ Remainder }}{\text{ Divsior }}$
Procedure to convert $\frac{23}{7}$ into mixed fraction as follows divide 23 by 7 as follows

$$\begin{gathered} 7\left)23\right(3 \\ 21 \\ \overline{ 2} \end{gathered}$$

We have quotient 3 and remainder 2 when 23 divided by 7.

Therefore required fraction = Quotient $\frac{\text{ Re mainder }}{\text{ Divsior }}=3\frac{2}{7}$

Convert $\frac{58}{7}$ into mixed fraction

$$\begin{gathered} 7\left)58\right(8 \\ 56 \\ \overline{ 2} \end{gathered}$$

Required mixed fraction = $8\frac{2}{7}$

6. COMPARISON OF FRACTIONS
To compare two are more fractions, their denominators should be equal. If the denominator of given fractions are not equal, then change each one of the given fractions into an equivalent fractions with denominator equal to the L.C.M of the denominators of the given fractions. Now the new fractions are like fractions so that the comparison between two or more fractions is possible when they are like fractions.
Conditions for comparison of fractions
To compare given fraction we can use following conditions.
(i) Fractions with same denominator
Among the fractions with same denominator, the fraction with greater numerator is greater than the other.
Example:
For the fractions $\frac{2}{9},\frac{14}{9};\frac{14}{9}>\frac{2}{9}$ since both have same denominator and 14 > 2
(ii) Fractions with same numerator
Among two fractions with same numerator. The fraction with smaller denominator is greater than the other.
Eg: For the fractions $\frac{2}{9}$ and $\frac{2}{6};\frac{2}{6}>\frac{2}{9}$ since both have same numerator and 6<9

(iii) Fractions with different numerator and denominator
(A) When compare fractions with different numerator and different denominators, we change them into fractions by equating their denominators to L.C.M of denominators of given fractions and then compare numerators of like fraction by applying first condition.
Example:

For $\frac{4}{5},\frac{6}{7}$; L.C.M of 5, 7 is 35

Now $\frac{4}{5}=\frac{4\times 7}{5\times 7}=\frac{28}{35}; \frac{6}{7}=\frac{6\times 5}{7\times 5}=\frac{30}{35}$

Now $\frac{28}{35}, \frac{30}{35}$ are like fractions (since they have equal denominators) and 30 > 28

$\Rightarrow \frac{30}{35}>\frac{28}{35}\Rightarrow \frac{6}{7}>\frac{4}{5}$
(B) To compare fractions with different numerators and different denominators we can also use the following method for the fractions $\frac{a}{b},\frac{c}{d}$ find cross products ad and bc.
If ad > bc, then $\frac{a}{b}>\frac{c}{d};$ If ad < bc, then $\frac{a}{b}<\frac{c}{d}$; If ad = bc, then $\frac{a}{b}=\frac{c}{d}$

Example:
Compare the fractions $\frac{3}{5}$ and $\frac{8}{11}$ by considering cross multiplication

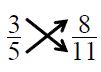
The products are 33, 40 and 40 > 33

$\Rightarrow 5\times 8>3\times 11\Rightarrow \frac{8}{11}>\frac{3}{5}$

Therefore $\frac{8}{11}>\frac{3}{5}$

7. ARRANGING FRACTIONS IN ASCENDING AND DESCENDING ORDER
Ascending order of fractions means arranging fractions from smaller value to greater value and descending order of fractions means arranging fractions from greater value to smaller value. This can be done by comparison of fractions.
Examples:
Rearrange the following fractions in ascending order and descending order $\frac{2}{3},\frac{4}{5},\frac{7}{15},\frac{11}{20},\frac{23}{30}$

Here the given fractions have different numerators and different denominators.

L.C.M. of 3, 5, 15, 20, 30 = 2 × 3 × 10 = 60

Therefore $\frac{2}{3}=\frac{2\times 20}{3\times 20}=\frac{40}{60};$ $\frac{4}{5}=\frac{4\times 12}{5\times 12}=\frac{48}{60};$ $\frac{7}{15}–\frac{7\times 4}{15\times 4}–\frac{28}{60}$; $\frac{11}{20}–\frac{11\times 3}{20\times 3}–\frac{33}{60}$ and $\frac{23}{30}=\frac{23\times 2}{30\times 2}=\frac{46}{60}$.

Since 28 < 33 < 40 < 46 < 48

$\Rightarrow \frac{28}{60}<\frac{33}{60}<\frac{40}{60}<\frac{46}{60}<\frac{48}{60}$   $\Rightarrow \frac{7}{15}<\frac{11}{20}<\frac{2}{3}<\frac{23}{30}<\frac{4}{5}$

Therefore the ascending order of given fractions is $\frac{7}{15},\frac{11}{20},\frac{2}{3},\frac{23}{30},\frac{4}{5}$ and the descending order of given fraction is $\frac{4}{5},\frac{23}{30},\frac{2}{3},\frac{11}{20},\frac{7}{15}$.

8. FUNDAMENTAL OPERATIONS (+, -, ×, ÷) ON FRACTIONS
(i) Addition
Addition of two or more fractions is possible, when they are like fractions.
Addition of Like Fractions:
If the given set of fractions have same denominator (i.e., like fraction), then the numerator of sum of all fractions is the sum of numerators of given fractions and denominator is their common denominator.
Therefore sum of all like fractions = $\frac{\mathrm{Sum} \mathrm{of} \mathrm{all} \mathrm{Numerators} \mathrm{of} \mathrm{Fractions} }{\mathrm{Common} \mathrm{Denominator}}$

Example: $\frac{5}{6}+\frac{8}{6}+\frac{13}{6}+\frac{22}{6}=\frac{2–8–13–22}{6}=\frac{48}{6}=8$

Addition of Unlike Fractions:
Step1: We find L.C.M of denominators of all fractions.
Step2: Now convert each of the given fractions into equivalent like fractions by equating their denominators to L.C.M of denominators.
Step3: Now we can add all like fractions which are so obtained in Step2
Step4: Reduce the fraction obtained in Step3 into its lowest terms and convert it into mixed fractions if it is a improper fraction.
Examples:
Step1: Find the sum of $\frac{5}{9},\frac{8}{12},\frac{15}{16}$

Step2: Now $\frac{5}{9}=\frac{5\times 16}{9\times 16}=\frac{80}{144}$; $\frac{8}{12}=\frac{8\times 12}{12\times 12}=\frac{96}{144}$; $\frac{15}{16}=\frac{15\times 9}{16\times 9}=\frac{135}{144}$;

Step3: Now sum = $\frac{5}{9}+\frac{8}{12}+\frac{15}{16}=\frac{80+96+135}{144}=\frac{311}{144}$ is a improper fraction

Step4: Therefore $\frac{5}{9}–\frac{8}{12}+\frac{15}{16}=\frac{311}{144}=2\frac{23}{144}$

Addition of Mixed Fractions:
If given set of fractions are mixed fractions;
Step1: Convert each of the mixed fractions into an improper fraction.
Step2: Add all improper fractions using the procedure, either like fractions addition or unlike fractions addition.
Example:
Find the sum of $1\frac{2}{5}+2\frac{3}{5}+3\frac{4}{5}$
Method 1:
In above the addends are mixed fractions

$1\frac{2}{5}–\frac{7}{5}; 2\frac{3}{5}–\frac{13}{5}; 3\frac{4}{5}–\frac{19}{5}$

Now, $1\frac{2}{5}+2\frac{3}{5}–3\frac{4}{5}=\frac{7}{5}–\frac{13}{5}+\frac{19}{5}=\frac{39}{5}=7\frac{4}{5}$
Method 2:
$1\frac{2}{5}+2\frac{3}{5}–3\frac{4}{5}=(1+2+3)+\left(\frac{2+3+4}{5}\right)$

$=6–\frac{5}{5}+\frac{4}{5}$

$=6+1+\frac{4}{5}$

$=–7\frac{4}{5}$

Example:
Find sum of $1\frac{2}{3}+2\frac{3}{4}+3\frac{1}{5}$

Method 1:
In above addends are mixed fractions

$1\frac{2}{3}=\frac{5}{3}$;           $2\frac{3}{4}=\frac{11}{4}$;       $3\frac{1}{5}=\frac{16}{5}$

Now, $1\frac{2}{3}+2\frac{3}{4}+3\frac{1}{5}=\frac{5}{3}+\frac{11}{4}+\frac{16}{5}$

$=\frac{(5\times 20)\times (11\times 15)\times (16\times 12)}{60}$ = $\frac{100+165+192}{60}=\frac{457}{60}=7\frac{37}{60}$

Method 2:

$1\frac{2}{3}+2\frac{3}{4}+3\frac{1}{5}=(1+2+3)+\left(\frac{2}{3}–\frac{3}{4}+\frac{1}{5}\right)$

$=6+\frac{(2\times 20)+(3\times 15)+(1\times 12)}{60}$

$=6+\frac{(40+45–12)}{60}$ = $6+\frac{97}{60}=6+1\frac{37}{60}=7\frac{37}{60}$

II. Subtraction
Subtraction of Like Fractions
Difference of like fractions is a fraction which is having numerator as difference of numerator and denominators is common denominator.
Therefore difference of like fraction = $\frac{\text{ Difference of Numerators }}{\text{ Common Denominator }}$

Examples:

$\frac{9}{13}–\frac{4}{13}=\frac{9–4}{13}=\frac{5}{13}$

$\frac{2}{3}–\frac{1}{5}$

Subtraction of Unlike Fractions
First we find L.C.M of denominators of given fractions.
Convert each of the given fraction into equivalent like fraction by equating their denominators to L.C.M of denominators.
Now we can find difference between like fractions so obtained.

Method 1 :

$\frac{2}{3}–\frac{1}{5}$

L.C.M of 3,5 = 15

$\frac{2}{3}=\frac{2\times 5}{3\times 5}=\frac{10}{15}$

$\frac{1}{5}=\frac{1\times 3}{5\times 3}=\frac{3}{15}$

$\frac{2}{3}–\frac{1}{5}=\frac{10}{15}–\frac{3}{15}=\frac{10–3}{15}=\frac{7}{15}$

Method 2 :

$\frac{2}{3}–\frac{1}{5}=\frac{(2\times 5)–(1\times 3)}{15}=\frac{10–3}{15}=\frac{7}{15}$

Subtraction of Mixed Fractions
While subtracting two or more mixed fractions, convert each of mixed fractions in to an improper fraction and then find the difference of fractions so obtained using any of the above methods.
Examples:

Find $3\frac{1}{6}–2\frac{1}{4}+4\frac{1}{3}–2\frac{1}{5}$

Since $3\frac{1}{6}=\frac{19}{6}; 4\frac{1}{3}=\frac{13}{3} 2\frac{1}{4}=\frac{9}{4}; 2\frac{1}{5}=\frac{11}{5}$

Now $3\frac{1}{6}–2\frac{1}{4}+4\frac{1}{3}–2\frac{1}{5}=\frac{19}{6}–\frac{9}{4}–\frac{13}{3}–\frac{11}{5}$

(Therefore L.C.M of 6, 4, 3, 5 = 60)

$=\frac{190–135+260–132}{60}$

(Since 60$÷$6 = 10; 60$÷$3 = 20; 60$÷$4 = 15; 60$÷$5 = 2)

$=\frac{450–267}{60}=\frac{186}{60}=3\frac{3}{60}\text{ or }3\frac{1}{20}$

Therefore  $3\frac{1}{6}–2\frac{1}{4}+4\frac{1}{3}–2\frac{1}{5}=3\frac{3}{60}\text{ or }3\frac{1}{20}$

III. Multiplication
Multiplication of two fractions is a fraction whose numerator is products of numerators of given fractions and denominators is product of denominators of given fractions, we can define it as follows:

Product of Fractions = $\frac{\text{ Product of their Numerators }}{\text{ Product of their Denominator }}$

i.e., for any two fractions $\frac{\mathrm{a}}{\mathrm{b}},\frac{\mathrm{c}}{\mathrm{d}},\frac{\mathrm{a}}{\mathrm{bz}}\times \frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{a}\times \mathrm{c}}{\mathrm{b}\times \mathrm{d}}\text{ or }\frac{\mathrm{ac}}{\mathrm{bd}}$

Example:

Multiplication of $\frac{2}{5}$ and $\frac{3}{8}$ is $\frac{2}{5}\times \frac{3}{8}=\frac{6}{40}=\frac{3}{20}$

For the multiplication of mixed fractions convert them into improper fractions and then consider multiplication.
Example:

$2\frac{3}{4}\times 1\frac{5}{6}=\frac{11}{4}\times \frac{11}{6}=\frac{121}{24}$

Reciprocal or Multiplicative Inverse of a Fraction

If the product of any two fractions is 1, then each one of them is called reciprocal or multiplicative inverse of other.
For the fraction $\frac{\mathrm{p}}{\mathrm{q}},\frac{\mathrm{q}}{\mathrm{p}},\frac{\mathrm{p}}{\mathrm{q}}\times \frac{\mathrm{q}}{\mathrm{p}}=1$

Therefore reciprocal of $\frac{\mathrm{p}}{\mathrm{q}}$ is $\frac{\mathrm{q}}{\mathrm{p}}$ and reciprocal of $\frac{\mathrm{q}}{\mathrm{p}}$ is $\frac{\mathrm{p}}{\mathrm{q}}$

Examples:

The reciprocal of $\frac{5}{6}$ is $\frac{6}{5}$

The reciprocal of $1\frac{2}{3}$ is $\frac{3}{5}$ $\left(\text{ Since }1\frac{2}{3}=\frac{5}{3}\right)$

The reciprocal of 2 is $\frac{1}{2}$ $\left(\text{ Therefore }2=\frac{25}{1}\right)$

IV. Division
To divide one fraction by another fraction, we multiply the dividend fraction by the reciprocal of the divisor.
Examples:

$\frac{3}{5}÷\frac{2}{3}=\frac{3}{5}\times \frac{3}{2}=\frac{9}{10}$

$1\frac{2}{3}÷2\frac{2}{5}=\frac{5}{3}÷\frac{12}{5}=\frac{5}{3}\times \frac{5}{12}=\frac{25}{36}$

Note:
For any fraction $\frac{a}{b},1\times \frac{a}{b}=\frac{a}{b}\times 1=\frac{a}{b}$ and $1÷\frac{a}{b}=\frac{b}{a}; \frac{a}{b}÷1=\frac{a}{b}; \frac{a}{b}\times 0=0\times \frac{a}{b}=0$

Every non zero fraction or rational number has multiplicative inverse.
Zero does not have multiplicative inverse.